Binomialkoeffizient einfach erklärt
Hier lernst du alles über den Binomialkoeffizienten! Hast du keine Lust zu lesen? Dann schau doch einfach unser Video !
Inhaltsübersicht
Binomialkoeffizient Erklärung
Den Binomialkoeffizienten brauchst du, um in der Stochastik oder Kombinatorik die Anzahl von Möglichkeiten zu berechnen.
Stell dir vor, du möchtest aus einem Topf mit drei Kugeln zwei Kugeln ziehen, ohne sie dabei zurückzulegen. Die Kugeln sind mit den Buchstaben A, B und C beschriftet. Du kannst sie also unterscheiden, aber die Reihenfolge ist dir dabei egal. Ob du zuerst Kugel A ziehst und dann B oder andersrum, ist nicht wichtig. Für dich zählt nur das Endergebnis. Hier brauchst du dann den Binomialkoeffizienten. Der berechnet die Anzahl der möglichen Kombinationen und du schreibst ihn:
![Rendered by QuickLaTeX.com \[{\textcolor{red}{3}\choose \textcolor{blue}{2}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5bc140a57f5c3ca9173db758748dbfb0_l3.png)
Du sprichst das dann so aus: „2 aus 3” oder „3 über 2”.
Der Binomialkoeffizient ist eine mathematische Funktion. Mit ihm kannst du bestimmen, wie viele Möglichkeiten es gibt, k Objekte aus n Elementen zu wählen. Dabei ist es wichtig, dass du ohne Beachtung der Reihenfolge und ohne Zurücklegen auswählst. Du schreibst ihn so:
![Rendered by QuickLaTeX.com \[{\textcolor{red}{n}\choose \textcolor{blue}{k}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-042269dae60a6285042ebf8a4a00e422_l3.png)
Schau dir jetzt am besten mal an, wie du den Binomialkoeffizienten berechnen kannst.
Binomialkoeffizient berechnen
Die Formel für den Binomialkoeffizienten sieht so aus:
![Rendered by QuickLaTeX.com \[{\textcolor{red}{n}\choose \textcolor{blue}{k}}=\cfrac{\textcolor{red}{n}!}{\textcolor{blue}{k}!\cdot(\textcolor{red}{n}-\textcolor{blue}{k})!}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-47656ce36e25ec4592ea5162c0b61886_l3.png)
Das Ausrufezeichen „!“ steht für Fakultät . Bei 9! rechnest du zum Beispiel
9! = 9 · 8 · 7 · 6 · ….· 2 · 1
Schau dir dafür nochmal das Beispiel vom Anfang an:
![Rendered by QuickLaTeX.com \[{\textcolor{red}{3}\choose \textcolor{blue}{2}}=\cfrac{\textcolor{red}{3}!}{\textcolor{blue}{2}!\cdot(\textcolor{red}{3}-\textcolor{blue}{2})!}=\cfrac{3!}{2!\cdot1!}=3\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7113999314990d6d831b54826365faf2_l3.png)
Du hast also 3 verschiedene Möglichkeiten! Wie sieht es aus, wenn du eine Urne mit 10 verschiedenen Kugeln hast und 3 daraus ziehen willst, ohne dabei eine Kugel zurückzulegen? Du kannst wieder den Binomialkoeffizienten benutzen:
![Rendered by QuickLaTeX.com \[{\textcolor{red}{10}\choose \textcolor{blue}{3}}=\cfrac{\textcolor{red}{10}!}{\textcolor{blue}{3}!\cdot(\textcolor{red}{10}-\textcolor{blue}{3})!}=\cfrac{10!}{3!\cdot7!}=120\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-114348cf4284bf95982519c0a4765a3a_l3.png)
Es gibt also in dem Fall 120 Möglichkeiten.
Merk dir: Den Binomialkoeffizienten brauchst du immer dann, wenn du die Reihenfolge nicht beachtest und nicht zurücklegst (oder keine Wiederholung erlaubt ist).
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Binomialkoeffizient Taschenrechner
Natürlich brauchst du nicht immer die lange Formel. Bei deinem Taschenrechner kannst du den Binomialkoeffizienten mit der Taste „nCr“ bestimmen. Zuerst tippst du die obere Zahl deines Binomialkoeffizienten ein und drückst dann auf die Taste „nCr„: Auf deinem Display sollte dann ein „C“ stehen. Wenn du jetzt noch die untere Zahl eintippst und „=“drückst, kannst du so n über k im Taschenrechner bestimmen:
Schau dir jetzt nochmal ein Anwendungsbeispiel an.
Binomialkoeffizient Beispiel
Anna, Jakob, Miriam und Lukas spielen fast jeden Tag zusammen Basketball. Die 4 Freunde wollen an der Basketball Stadtmeisterschaft teilnehmen. Es dürfen aber leider nur 2 von ihnen mitmachen. Die 4 Freunde fragen dich, ob du entscheiden kannst, wer teilnehmen sollte. Du findest, dass alle vier Freunde gleich gut spielen und entscheidest dich zu losen. Du schreibst jeweils einen Namen auf einen Loszettel und vermischt die Zettel in einer kleinen Box.
Dabei fragst du dich, wie viele verschiedene Zweierteams überhaupt ausgelost werden könnten. Kannst du hier den Binomialkoeffizienten verwenden? Du erinnerst dich vielleicht noch an die Erklärung von weiter oben. Zuerst prüfst du, ob die Auslosung ohne Beachtung der Reihenfolge passiert. Ja! Es ist egal, ob du Miriam als Erstes oder als Zweites ziehst. Es zählt nur, dass sie überhaupt dabei ist!
Dann musst du noch überlegen, ob du ohne Zurücklegen lost. Auch das stimmt! Du kannst schließlich nicht zweimal die gleiche Person auslosen. Also weißt du, dass du den Binomialkoeffizienten verwenden kannst. Für n setzt die Gesamtanzahl ein, also 4. Du willst genau 2 Lose aus deiner Box ziehen, also ist k gleich 2:
![Rendered by QuickLaTeX.com \[{\textcolor{red}{n}\choose \textcolor{blue}{k}}={\textcolor{red}{4}\choose \textcolor{blue}{2}}=\cfrac{\textcolor{red}{4}!}{\textcolor{blue}{2}!\cdot(\textcolor{red}{4}-\textcolor{blue}{2})!}=\cfrac{4!}{2!\cdot2!}=6\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-061fbc258a39af55a3e584c83b697ab0_l3.png)
Es gibt also genau 6 verschiedene zweier Teams, die du auslosen könntest!
Binomialkoeffizient Rechenregeln
Du solltest noch ein paar wichtige Regeln kennen, wenn du mit dem Binomialkoeffizienten rechnest:
-
 : Wenn das nicht der Fall ist, hast du keine Lösung!
: Wenn das nicht der Fall ist, hast du keine Lösung! -
 : Der Binomialkoeffizient ist immer positiv
: Der Binomialkoeffizient ist immer positiv -
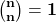 : Wenn k gleich n ist, ist dein Wert immer 1
: Wenn k gleich n ist, ist dein Wert immer 1 -
 : Wenn k gleich 0 ist, ist dein Wert immer 1
: Wenn k gleich 0 ist, ist dein Wert immer 1
Jetzt kennst du auch die wichtigsten Regeln bei n über k. Wenn du noch mehr darüber erfahren willst, sieh‘ dir doch unser Experten-Video zum Binomialkoeffizienten an.
Pascalsches Dreieck
Du kennst jetzt schon 2 Methoden, um den Binomialkoeffizienten zu bestimmen. Es gibt aber noch eine weitere Möglichkeit! Mit dem Pascalschen Dreieck kannst du den Binomialkoeffizienten ganz einfach ablesen. Schau dir doch gleich unser Video dazu an.

