Video

Quiz

t Verteilung

Wichtige Inhalte in diesem Video

Student t Verteilung

t Verteilung Tabelle

Dieser Artikel befasst sich mit der t Verteilung. Es wird geklärt was die Student t Verteilung ist und wann sie in der Statistik verwendet wird. Außerdem zeigen wir dir wie man mit der t Verteilung Tabelle umgeht.

Als Schüler oder Student lernst du gerne effektiv? Kein Problem, unser Video erklärt dir die studentische t Verteilung auf studentisch!

Inhaltsübersicht

Student t Verteilung

im Videozur Stelle im Video springen

Die studentsche t Verteilung, oder einfach auch nur t Verteilung, ist eine Wahrscheinlichkeitsverteilung, welche hauptsächlich im Zusammenhang mit Hypothesentests und Konfidenzintervallen angewendet wird. Student ist das Pseudonym, das der Entwickler der Verteilung William Sealy Gosset verwendete.

t-Verteilung, t Verteilung, Student t Verteilung, Studensche Vertielung, studentische verteilung — Student t Verteilung

Die Verteilung lässt sich folgendermaßen definieren:

$T=\frac{Z}{\sqrt{\frac{1}{n}\chi^2}}$

Wobei Z standardnormalverteilt ist und Chi Quadrat von Z unabhängig und, wer hätte es gedacht, Chi Quadrat verteilt sein muss. Falls dir die Begriffe Standardnormalverteilung und Chi Quadrat Verteilung noch nichts sagen, schau dir schnell unsere jeweiligen Videos dazu an.

Des Weiteren gilt:

t-Verteilung, t Verteilung berechnen, t verteilung Erwartungswert, t Verteilung Varianz — t Verteilung

t Verteilung Normalverteilung

Wir verwenden die Student Verteilung, wenn wir die Varianz, die wir zur Standardisierung in die Normalverteilung benötigen, nicht kennen. Ist das der Fall, müssen wir mit der Stichprobenvarianz s^2 rechnen Das ist in der Realität eigentlich immer der Fall, denn es ist uns meistens nicht möglich, alle Daten eines Datensatzes zu betrachten. Wir müssen uns also mit einer mehr oder weniger großen Stichprobe zufriedengeben.

t Verteilung Freiheitsgrade

Je größer unsere betrachtete Stichprobe ist, umso höher wird auch die Anzahl der Freiheitsgrade ist. Außerdem gilt dass je größer der Stichprobenumfang wird, desto schmaler wird auch der Graph der t Verteilung. Ab einem n > 30 kann man approximativ von der standardisierten Normalverteilung ausgehen.

t-Verteilung, t Verteilung Freiheitsgrade,t Verteilung Normalverteilung — t Verteilung Freiheitsgrade

t Verteilung Tabelle

im Videozur Stelle im Video springen

Na bravo! Der Erwartungswert lässt sich leicht erschließen und die Varianz sehr einfach berechnen, aber wie bitte sollst du auf $f\left(x\right)$ kommen? Du hast Glück, denn, wie bei den meisten Verteilungen, verwenden wir auch hier eine Verteilungstabelle. Das heißt für dich: Du brauchst erstmal gar nichts auszurechnen.

n\p	0,65	0,7	0,75	0,8	0,85	0,9	0,95	0,975	0,99	0,995
1	0.51	0.727	1	1.376	1.963	3.078	6.314	12.706	31.821	63.656
2	0.445	0.617	0.816	1.061	1.386	1.886	2.92	4.303	6.965	9.925
3	0.424	0.584	0.765	0.978	1.25	1.638	2.353	3.182	4.541	5.841
4	0.414	0.569	0.741	0.941	1.19	1.533	2.132	2.776	3.747	4.604
5	0.408	0.559	0.727	0.92	1.156	1.476	2.015	2.571	3.365	4.032
6	0.404	0.553	0.718	0.906	1.134	1.44	1.943	2.447	3.143	3.707
7	0.402	0.549	0.711	0.896	1.119	1.415	1.895	2.365	2.998	3.499
8	0.399	0.546	0.706	0.889	1.108	1.397	1.86	2.306	2.896	3.355
9	0.398	0.543	0.703	0.883	1.1	1.383	1.833	2.262	2.821	3.25
10	0.397	0.542	0.7	0.879	1.093	1.372	1.812	2.228	2.764	3.169
11	0.396	0.54	0.697	0.876	1.088	1.363	1.796	2.201	2.718	3.106
12	0.395	0.539	0.695	0.873	1.083	1.356	1.782	2.179	2.681	3.055
13	0.394	0.538	0.694	0.87	1.079	1.35	1.771	2.16	2.65	3.012
14	0.393	0.537	0.692	0.868	1.076	1.345	1.761	2.145	2.624	2.977
15	0.393	0.536	0.691	0.866	1.074	1.341	1.753	2.131	2.602	2.947
16	0.392	0.535	0.69	0.865	1.071	1.337	1.746	2.12	2.583	2.921
17	0.392	0.534	0.689	0.863	1.069	1.333	1.74	2.11	2.567	2.898
18	0.392	0.534	0.688	0.862	1.067	1.33	1.734	2.101	2.552	2.878
19	0.391	0.533	0.688	0.861	1.066	1.328	1.729	2.093	2.539	2.861
20	0.391	0.533	0.687	0.86	1.064	1.325	1.725	2.086	2.528	2.845
21	0.391	0.532	0.686	0.859	1.063	1.323	1.721	2.08	2.518	2.831
22	0.39	0.532	0.686	0.858	1.061	1.321	1.717	2.074	2.508	2.819
23	0.39	0.532	0.685	0.858	1.06	1.319	1.714	2.069	2.5	2.807
24	0.39	0.531	0.685	0.857	1.059	1.318	1.711	2.064	2.492	2.797
25	0.39	0.531	0.684	0.856	1.058	1.316	1.708	2.06	2.485	2.787
30	0.389	0.53	0.683	0.854	1.055	1.31	1.697	2.042	2.457	2.75

Verteilungstabelle Besonderheiten

Die Tabelle hat allerdings zwei Besonderheiten. Zum einen geht sie nur bis zu einem n = 30. Das ist aber kein Problem, denn ab einem n > 30 verwenden wir ja eh approximativ die Normalverteilung. Zum anderen wirst du in der Tabelle nur $\alpha\geq\ 0,6$ finden.

t-Verteilung, t verteilung tabelle, t-verteilung tabelle, tabelle t verteilung, student t verteilung tabelle — t Verteilung Tabelle

Quiz zum Thema t Verteilung

t Verteilung berechnen

Suchen wir also für ein n=10 und ein $\alpha = 0,7$ unseren x-Wert, dann müssen wir lediglich das Ergebnis aus der richtigen Zeilen-Spalten-Kombination ablesen.

$t_{10;0,7}=\ 0,542$

Wir erhalten also eine Lösung von 0,542.

Wie gesagt, kein Rechnen, sondern bloßes Ablesen des Ergebnisses.

Ein bisschen komplizierter wird es allerdings, wenn du mit einem 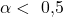$\alpha<\ 0,5$ arbeitest. Denn hier existieren keine Spalten. Für ein $\alpha\ =\ 0,5$ ist die Lösung einleuchtend. Jede studentsche Verteilung ist nämlich entlang der y-Achse achsensymmetrisch. Der Wert einer Verteilung mit $\alpha\ =\ 0,5$ ist deshalb auch immer gleich null. Es ist genau die Mitte der Verteilung und verdeutlicht auch nochmal, weshalb wir immer einen Erwartungswert von null haben.

t-Verteilung — Die t-Verteilung ist achsensymmetrisch zur y-Achse

Aber wie sieht es jetzt mit einem $\alpha$ links von unserem Erwartungswert aus? Die allgemeine Formel zur Lösung dieses Problems lautet:

$t_{n;\alpha}=-\ t_{n;1-\alpha}$

Haben wir erneut ein n=10 und diesmal beispielsweise das $\alpha\ = 0,3$ , sieht die Formel also so aus:

$t_{10;0,3}={-t}_{10;1-0,3}={-t}_{10;0,7}=-0,542$

Durch einen kurzen Blick in die Tabelle merken wir, dass wir das Ergebnis schon kennen. Es ist das Gleiche wie für ein $\alpha\ = 0,7$ , nur das es diesmal negativ ist.

t-Verteilung — Das Ergebnis ist das gleiche, nur negativ

Prima! Jetzt bist du in Sachen t Verteilung bestens informiert und kannst dich endlich wieder mit deiner Oma zum Tee trinken verabreden. Viel Spaß dabei!

zur Videoseite: t Verteilung

Stetige Gleichverteilung

Normalverteilung

Standardnormalverteilung

Exponentialverteilung

Chi Quadrat Verteilung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .