Binärer Suchbaum
Binäre Suchbäume sind als Datenstruktur Teil der theoretischen Informatik. Hierfür wird in diesem Beitrag alles Wichtige zur allgemeinen Definition und der Terminologie erklärt. Darauf aufbauend zeigen wir dir, wie man einen binären Suchbaum erstellen kann. Im Anschluss gibt es alle wichtigen Informationen zu Operationen, die anhand von verschiedenen Beispielen erläutert werden (z.B. Binärer Suchbaum Löschen). Danach gibt es alle wichtigen Fakten zur Komplexität. Am Ende folgt ein Quellcode für binäre Suchbäume in Java.
Inhaltsübersicht
Binäre Suchbäume – Definition & Terminologie
Bei binären Suchbäumen (englisch Binary Search Tree) handelt es sich um eine Datenstruktur, die eine Mischung zwischen einem Suchbaum und einem Binärbaum darstellt. Im Gegensatz zum klassischem Binärbaum hat ein binärer Suchbaum die Elemente im linken Teilbaum, die kleiner als die Wurzel sind. Als Gegensatz dazu sind alle Elemente im rechten Unterbaum größer als die Wurzel. Diese Eigenschaft spiegelt sich in jedem Knoten wider. Es gilt, dass jeder Nachkomme auf der linken Seite kleiner gleich oder auf der rechten Seite größer gleich des Knotes selbst sein müssen, was bedeutet, dass eine Totalordnung entsprechend des Ordnungskriteriums vorliegen muss.
Binären Suchbaum erstellen
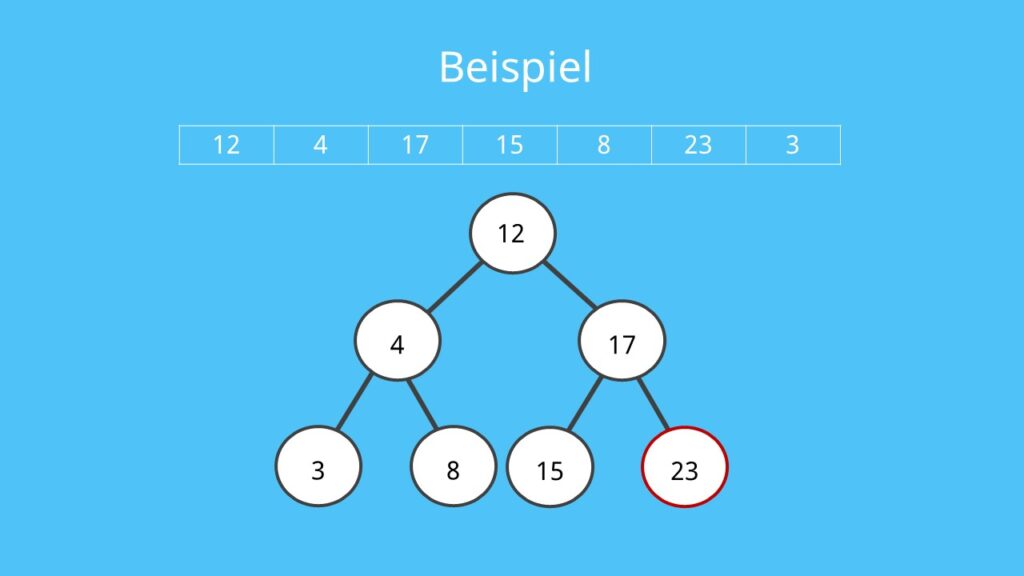
Im folgenden Beispiel wird eine Liste aus Zahlen als binärer Baum gespeichert. Array = 12, 4, 17, 15, 8, 23, 3.
Mit der Liste kann man nun einen binären Suchbaum erstellen. Der Baum baut sich mit der ersten Zahl 12 als Wurzel auf. Die restlichen Elemente werden entsprechend ihres Werts nach und nach in den linken oder rechten Unterbaum als entsprechende Nachfolger an ihrer richtigen Position eingefügt. Am Ende erhält man einen fertigen binären Suchbaum, der sich nach dem Einfügen wie folgt darstellen lässt:
Die Funktionsweise des Erstellens, lässt sich mit der Binärer Suchbaum Insert-Operation gleichsetzen. Entsprechend können also auch neue Zahlen in einem Array in den Binären Suchbaum eingefügt werden.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Operationen
Der abstrakte Datentyp lässt sich durch verschiedene Operationen definieren:
- Init(): Erstellen eines leeren binären Suchbaums.
- Insert(n): Das Element n wird in Form eines neuen Knotens entsprechend der Totalordnung in den rechten oder linken Teilbaum hinzugefügt.
- Remove(n): Das Element n wird gelöscht.
- Member(n): Sollte das Element n im Baum existent sein, wird der Wert TRUE zurückgeliefert, ansonsten FALSE.
- Empty(): Solange der binäre Suchbaum leer ist, wird der Wert True zugeliefert, ansonsten FALSE.
Binärer Suchbaum Beispiel
Anhand des vorherigen Beispiels des Erstellens/Einfügens werden im Folgenden die Operationen Suchen und Löschen durchgeführt.
Unser Array besteht dabei also aus den folgenden Zahlenwerten: 12, 4, 17, 15, 8, 23, 3.
Auf Basis der kleiner-größer-Vergleiche, kann der Baum einen direkten Pfad bei der Suche durchlaufen. Exemplarisch wird nun nach der 23 gesucht, dabei beginnt die Suche bei der Wurzel 12. Da die 23 größer als die 12 ist, wandert der Suchvorgang automatisch in den rechten Teilbaum. Im nächsten Schritt wir der Wert 17 verglichen, der auch wieder kleiner ist, als das gesuchte Element. Dadurch geht der Pfad automatisch wieder nach rechts, wodurch die 23 bereits erreicht wird.
Suche
Jedoch kann sich der Ansatz bei der allgemeinen Suche innerhalb eines binären Suchbaums unterscheiden. In diesem Beispiel ist kein Duplikat vorhanden. Deshalb muss von vornherein festgelegt werden, ob doppelte Einträge im Baum erlaubt sind. Wenn bei dem Algorithmus auf keinen Fall Duplikate aufgenommen werden sollen, handelt es sich um eine rekursive Suche ohne Duplikat. Im Fall, dass das Ordnungkriterium nach dem größer gleich/kleiner gleich Prinzip arbeitet, sind entsprechende Duplikate zulässig. Heißt also, dass Einträge desselben Werts erlaubt sind. Hierbei ist es in der Praxis vorteilhaft, wenn die Suche nicht direkt beim ersten Fund abgebrochen wird, sondern der Baum die zugehörigen Blätter nach möglichen Duplikaten untersucht.
Binärer Suchbaum Löschen – Knoten ohne Nachfolger
Das Löschen ohne Nachfolger stellt sich als ziemlich einfach heraus. Da dabei keine Auswirkungen auf die restlichen Knoten vorhanden sind, kann das entsprechende Element einfach entfernt werden, ohne das weitere Schritte benötigt werden. Diese wäre der Fall, wenn beispielsweise die Zahl 3 aus dem Array gelöscht werden soll.
Binärer Suchbaum Löschen – Knoten mit Nachfolger
Bei einem Löschen eines Knotens mit Nachfolger, muss ein zusätzlicher Schritt eingeleitet werden. Nach dem Entfernen des zu löschenden Elements, übernimmt der Nachfolger im Anschluss dessen Position. Als Beispiel wird aus dem Array der Wert 4 gelöscht. Dadurch positioniert sich der einzige Nachfolger 8 automatisch auf den ursprünglichen Platz des Elements 4.
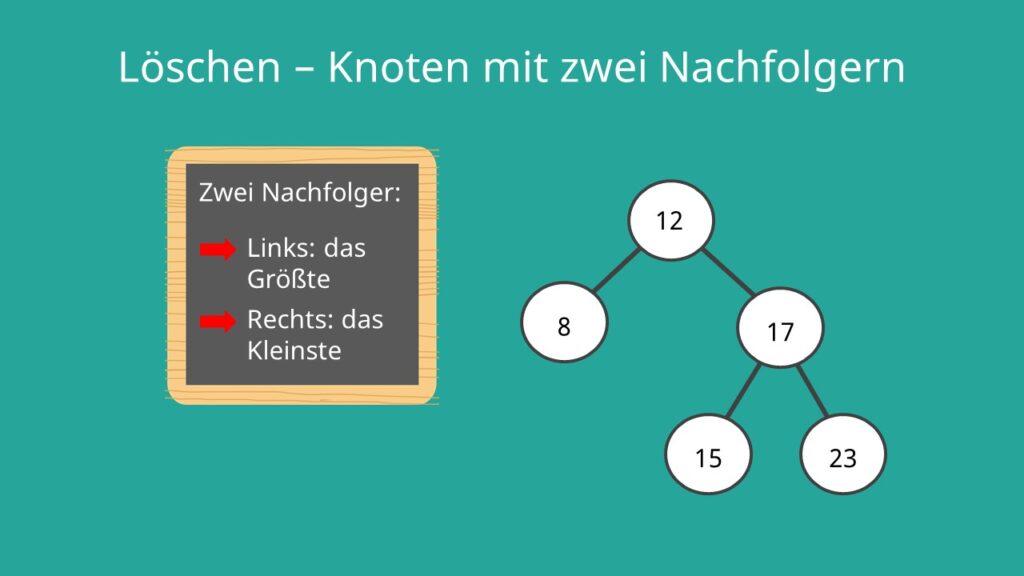
Wenn der zu löschende Knoten zwei Nachfolger besitzt, kann dieser entweder von dem größten Nachfolger der linken Seite ersetzt werden, oder vom dem kleinsten Nachfolger der rechten Seite. Zur Veranschaulichung wird nun der Zahlenwert 12 aus dem binären Suchbaum gelöscht. Da es sich hierbei um die Wurzel des Baums handelt, ergeben sich für die neue, potenzielle Wurzel, die Werte 8 und 15. Die 8 ist der größte Wert des linken Teilbaums und die 15 entspricht dem kleinsten Wert des rechten Teilbaums.
Für die Neupositionierung gibt es keine strikten Vorgaben. Heißt also, dass beide Elemente die Wurzel ersetzten dürfen. Um den Baum besser auszugleichen und dadurch eine bessere Laufzeitkomplexität zu schaffen, wird in diesem Beispiel der Wert 15 als neue Wurzel gesetzt.
Komplexität
Der Name „Suchbaum“ lässt sich darauf zurückführen, dass das Auffinden von Daten sehr schnell funktioniert. Durch die Funktionsweise der kleiner-größer-Vergleiche, können binäre Suchbäume einen direkten Pfad ablaufen, anstatt den ganzen Baum durchsuchen zu müssen.
Dadurch ergibt sich eine allgemeine Laufzeitkomplexität von $O(N) = log N$. Dabei wird von einem Höhen-balancierten Suchbaum ausgegangen.
Die Suchoperation kann dabei aber im Worst Case linear abhängig von der Höhe h des Baumes sein. Daraus ergibt sich eine Laufzeit von $O(h)$. Zurückzuführen ist dieser Fakt auf dem einfach zu verstehenden Prinzip des Vergleichs. Basierend auf unserem Ausgangsbeispiel werden maximal 2 Vergleiche benötigt, bis der gesuchte Wert gefunden werden kann. Deshalb empfiehlt es sich, beide Seiten ähnlich groß aufzubauen, um möglichst viel Zeit einsparen zu können.
Binärer Suchbaum Java
Binärer Suchbaum Java-Implementierung:
public class knoten
{
public int wert;
public knoten links, rechts;
public wert(int n)
{
wert = n;
links = null;
rechts = null;
}
public void show()
{
System.out.println(„“+wert);
}
}
public class binaerersuchbaum
{
knoten root;
public binaerersuchbaum()
{
root = new knoten(100);
root.links = new knoten(50);
root.rechts = new knoten(150);
}
}