Mergesort
Du willst wissen was der Mergesort ist und wie er funktioniert? Hier zeigen wir dir eine ausführliche Erklärung mit Hilfe eines Beispiels. Im Anschluss erfährst du, welcher Algorithmus hinter dem Sortierverfahren steckt und wie er als Pseudocode aussehen kann. Danach zeigen wir dir einen Mergesort Java-Code und eine mögliche Implementierung in Python. Am Ende erfährst du alle wichtigen Fakten zur Mergesort Laufzeit und was hinter der Erweiterung „2-Wege-Mergesort“ steckt.
Inhaltsübersicht
Mergesort: Erklärung
Der Mergesort gehört zu den stabilen Sortieralgorithmen. Er leitet sich im Allgemeinen vom englischen „merge“, also verschmelzen und „sort“, dem sortieren ab. Der Sinn dahinter ist einfach nur, dass der Algorithmus die vorhandenen Daten als eine gesamte Liste betrachtet, die er dann in kleinere Listen unterteilt. Man kann also sagen, er zerlegt ein Gesamtproblem in mehrere Teilprobleme und löst diese dann Stück für Stück. Im Endeffekt setzt er sie dann zum Schluss zu einer Gesamtlösung zusammen. Heißt also verallgemeinert, dass der Algorithmus nach dem Grundsatz teile- und herrsche arbeitet. Das Teile-und-herrsche-Verfahren (englisch divide and conquer) stellt in der Informatik ein Paradigma für den Entwurf eines effizienten Algorithmus dar.
Funktionsweise
Die Funktionsweise lässt sich ganz einfach in drei Schritten erklären:
- Du hast eine Liste und zerlegst sie in zwei Hälften. Die Unterteilung setzt du solange fort, bis nur noch ein Element in einer Menge vorhanden ist.
- Dann sortierst du alle Teilstücke für sich. Hier also alphabetisch von A nach Z.
- Anschließend müssen die Hälften dann nach dem Suchkriterium zu einer Menge vermischt. Heißt also, dass wir hier auch wieder alphabetisch zusammenführen müssen. Zum Schluss haben wir dann unsere sortierte Liste.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Veranschaulichung der Funktionsweise
Das Bild illustriert dabei die drei wesentlichen Schritte des Teile-und-herrsche-Prinzips: Unterteilen, Sortierten und Verschmelzen.
Mergesort Beispiel
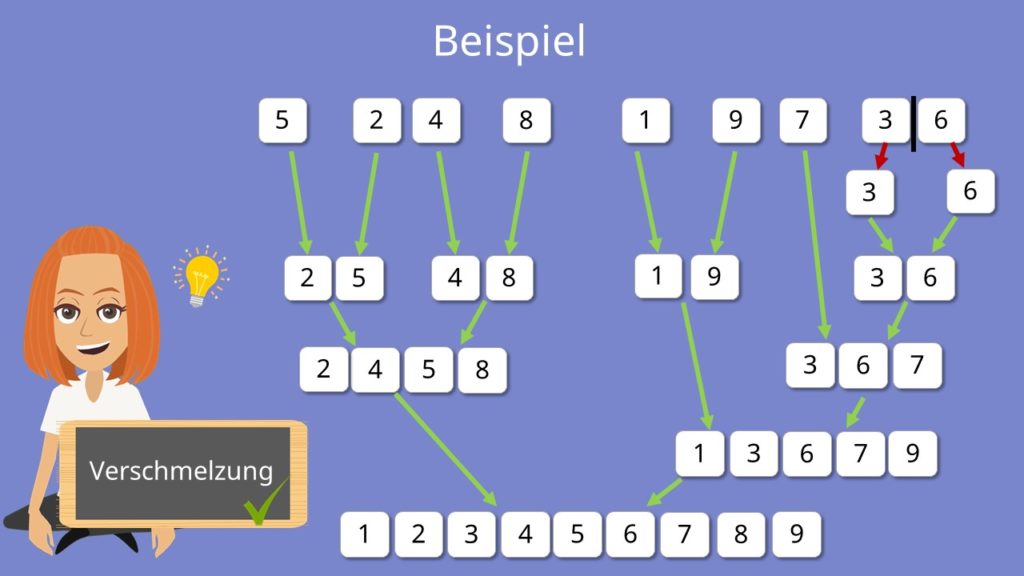
Aber schauen wir uns das doch lieber mal an einem ausführlicheren Beispiel an. Wir wollen dieses Array sortieren: [5] [2] [4] [8] [1] [9] [7] [3] [6]
Dafür zerteilen wir ihn also erstmal in der Mitte in zwei Teile. So haben wir auf der linken Seite vier und auf der rechten Seite fünf Elemente. Diese werden wieder halbiert, sodass wir drei Teile bestehend aus zwei Elementen haben und dann noch ein Teil bestehend aus drei Elementen. Wir halbieren nochmal und erhalten lauter einzelne Elemente, abgesehen von der 3 und der 6. Diese müssen noch einmal einzeln getrennt werden. Fertig.
Dann können wir nun also mit der Verschmelzung beginnen. Dabei werden immer zwei benachbarte Teile miteinander verbunden und dabei direkt sortiert. Wir packen also die 5 und die 2 zusammen und bringen sie direkt in die richtige Reihenfolge, also erst die 2, dann die 5. Das gleiche machen wir auch mit der 4 und der 8. Die sind schon richtig sortiert, also können wir uns das nächste Paar ansehen. Auch die 1 und die 9 sind sortiert. Dann fehlen noch die 7, die 3 und die 6. Da eine Zahl somit keinen Nachbar hat, verschmelzen wir erstmal nur die 3 und die 6 miteinander.
So, jetzt können wir wieder von links beginnen. Wir fügen 2 und 5 mit der 4 und der 8 zusammen. Dafür betrachten wir die jeweils ersten Elemente der Arrays miteinander. Die 2 ist kleiner als die 4 und wird ausgewählt. Dann wird die 5 mit der 4 verglichen und wir wählen die 4. Schließlich vergleichen wir noch die 5 mit der 8 und schreiben zuerst die 5 und dann die 8 in das neue Array.
Dasselbe machen wir nur mit der 7, der 3 und der 6. Zum Schluss müssen dann noch die letzten beiden Teile verschmolzen und geordnet werden und wir erhalten zum Schluss die sortierte Liste. Ziemlich einfach, oder?
Mergesort Pseudocode
Aber wie können wir den Algorithmus nun als verbalen Pseudocode darstellen? Der Algorithmus lässt sich in zwei Funktionen beschreiben, dafür wird zuerst einmal die Liste a eingegeben und in eine linke und rechte Hälfte halbiert. Für beide Seiten soll dann jeweils die Methode merge_sort ausgeführt werden (solange die Listen größer gleich 1 sind) und die verschmolzene sortierte Liste mit der Funktion verschmelzen zurückgegeben werden.
Mergesort Pseudocode – Unterteilen
Algorithmus:
merge_sort (Liste a)
Falls die Liste a <= 1 ist, soll die Liste antworten – sonst
soll die Liste in linke Liste l und rechte Liste r halbiert werden.
l = merge_sort(l)
r = merge_sort(r)
zurückgeben verschmelze (l,r)
Pseudocode:
merge_sort (Liste a)
if a <= 1
do
int mitte = a.lenght / 2
int l -> i <= mitte – 1
int r -> i >= array.length – mitte – 1
l = merge_sort(l)
r = merge_sort(r)
return verschmelze(l,r)Mergesort Pseudocode – Verschmelzen
Algorithmus:Verschmelze (linkeListe l,rechteListe r) zu einer neuen Liste n, solange die linke und rechte Liste nicht leer ist. Falls das erste Element der linken Liste kleiner gleich das erste Element der rechten Liste ist, dann füge das erste Element der linken Liste in die neue Liste ein und entferne es aus der linken Liste l. Ansonsten soll das erste Element der rechten Liste in die neue Liste hinten eingefügt werden und aus der rechten Liste r entfernt werden Solange die linke Liste l nicht leer ist, füge erstes Element der linken Liste in die neue Liste ein und entferne es aus der linken Liste l. Solange die rechte Liste r nicht leer ist, füge erstes Element der rechten Liste in die neue Liste ein und entferne es aus der rechten Liste r neue Liste n zurückgeben.
Pseudocode:
verschmelze (l, r)
int n
int indexl = length(l) – 1
int indexr = length(r) – 1
int indergebnis = 0
while indexl < l.length und indexr < r.length
if l[indexl] < r[indexr]
neul[indexergebnis] = l[indexl]
indexl += 1
else neul[indexergebnis] = r[indexr]
indexr += 1
indexergebnis += 1
while indexl < l.length
neul[indexergebnis] = l[indexl]
indexl += 1
indexergebnis += 1
while (indexr < r.length)
neul[indexergebnis] = r[indexr]
indexr += 1
indexergebnis += 1
return neulImplementierung: Mergesort Java
Hier kannst du einen beispielhaften Mergesort Java-Code sehen. Der Code ist dabei wie beim Pseudocode in zwei Methoden aufgeteilt – Unterteilen und Verschmelzen.
Java – Unterteilen
public static int[] merge_sort(int[] a)
{
if (a.length > 1) {
int mitte = (int)(a.length / 2);
int[] l = new int[mitte];
for (int i = 0; i <= mitte – 1; i++) {
l[i] = a[i];}
int[] r = new int[a.length – mitte];
for (int i = mitte; i <= a.length – 1; i++) {
r[i – mitte] = a[i];
}
l = merge_sort(l);
r = merge_sort(r);
return verschmelze(l, r);
}
else
{
return a;
}
}Java – Verschmelzen
private static int[] verschmelze(int[] l, int[] r)
{
int[] neul = new int[l.length + r.length];
int indexl = 0;
int indexr = 0;
int indexergebnis = 0;
while (indexl < l.length && indexr < r.length) {
if (l[indexl] < r[indexr]) {
neul[indexergebnis] = l[indexl];
indexl += 1;
} else {
neul[indexergebnis] = r[indexr];
indexr += 1;
}
indexergebnis += 1;
}
while (indexl < l.length) {
neul[indexergebnis] = l[indexl];
indexl += 1;
indexergebnis += 1;
}
while (indexr < r.length) {
neul[indexergebnis] = r[indexr];
indexr += 1;
indexergebnis += 1;
}
return neul;
}Implementierung: Mergesort Python
An dieser Stelle zeigen wir dir einen beispielhaften Mergesort Python-Code sehen. Der Code ist dabei wie beim Pseudocode in zwei Methoden aufgeteilt – Unterteilen und Verschmelzen.
Python – Teilen
def merge_sort(a):
if len(a) < 2:
return a
mitte = len(a) // 2
l = merge_sort(a[:mitte])
r = merge_sort(a[mitte:])
return verschmelze(l, r)
r = merge_sort(a[mitte:])
return verschmelze(l, r)Python – Verschmelzen
def verschmelze(l, r):
indexergebnis = []
indexl = indexr = 0
while indexl < len(l) and indexr < len(r):
if left[indexl] < right[indexr]:
indexergebnis.append(l[indexl])
indexl += 1
else:
indexergebnis.append(r[indexr])
indexr += 1
indexergebnis += l[indexl:]
indexergebnis += r[indexr:]
return indexergebnisMergesort Laufzeit
Doch nun zur Mergesort Laufzeit. Bei diesem Sortieralgorithmus ist die Laufzeitkomplexität immer gleich. Sowohl im Worst-, Best- und Average-Case beträgt die Komplexität  . Damit gehört er zu den schnellen Sortierverfahren. Der Aufwand setzt sich dabei so zusammen, dass erst die einzelnen Teile sortiert werden müssen und dann zusammen verschmolzen werden.
. Damit gehört er zu den schnellen Sortierverfahren. Der Aufwand setzt sich dabei so zusammen, dass erst die einzelnen Teile sortiert werden müssen und dann zusammen verschmolzen werden.
Grundsätzlich kann man sagen, dass der Algorithmus hinsichtlich seiner Komplexität dem Quicksort überlegen ist. Aber wenn du dir die Menge an Zwischenspeichern ansiehst, die bis zum Endergebnis benötigt werden, kannst du schon selbst erkennen, dass eine wahnsinnige große Menge an zusätzlichem Speicherplatz benötigt wird. Das muss natürlich in der Praxis beachtet werden.
2-Wege-Mergesort
Bezüglich dem Sortierverfahren kannst du auch immer wieder auf den Begriff Natural Mergesort oder natürliches 2-Wege-Mergesort treffen. Dabei handelt es sich um eine Erweiterung des Sortierverfahrens, die bereits vorhandene Teilfolgen, die vorsortiert sind, nutzt. Die vorsortierten Teilfolgen werden runs genannt. Diese müssen im ersten Durchgang bestimmt werden und gelten dann als Basis für den Mergevorgang.
Beispiel
Nehmen wir dafür einfach unser vorheriges Beispiel her, um uns das Ganze einmal genauer ansehen zu können.
Eingabeliste: [5] [2] [4] [8] [1] [9] [7] [3] [6]
Runs: [5] [2] – – – [4] – – – [8] [1] – – – [9] [7] [3] – – – [6]
Merge: [2] – – – [4] – – – [5] – – – [8] [1] – – – [7] – – – [9] [3] – – – [6]
Merge: [1] – – – [2] – – – [4] – – – [5] – – – [7] – – – [8] – – – [9] [3] – – – [6]
Merge: [1] – – – [2] – – – [3] – – – [4] – – – [5] – – – [6] – – – [7] – – – [8] – – – [9]
Durch den natürlichen 2-Wege-Mergesort kann sich der Sortieralgorithmus bezüglich der Best Case Komplexität auf O(n) steigern.