RSA Verschlüsselung
Die RSA Verschlüsselung ist ein asymmetrisches Verschlüsselungsverfahren , das häufig im Internet zur sicheren Datenübertragung eingesetzt wird. In diesem Beitrag lernst du, welche Eigenschaften die RSA Verschlüsselung besitzt, wie du eine Nachricht unter Verwendung des RSA Verfahrens verschlüsselst und wieder entschlüsselst und warum das Verfahren bis heute als sicher angesehen werden kann.
Du möchtest alles Wichtige zur RSA Verschlüsselung verständlich erklärt in wenigen Minuten erfahren? Dann schau unser Video an!
Inhaltsübersicht
RSA Verschlüsselung Definition
Die RSA Verschlüsselung ist ein von R. Rivest, A. Shamir und L. Adleman 1977 entwickeltes asymmetrisches Verschlüsselungsverfahren, welches sowohl zum Verschlüsseln als auch zum Erstellen einer digitalen Signatur eingesetzt wird. Das RSA Verfahren basiert auf einem Schlüsselpaar aus einem öffentlichen Schlüssel zum Verschlüsseln und einem privaten Schlüssel zum Entschlüsseln.
RSA Verfahren
Die Mathematiker R. Rivest, A. Shamir und L. Adleman versuchten 1976 die Annahmen einer Veröffentlichung von W. Diffie und M. Hellman im Bereich der Public-Key Kryptographie zu widerlegen. Dabei fanden sie ein Verfahren, das nach ihrer Einschätzung nicht angreifbar ist. Dieses Verfahren wurde dann nach ihren Entdeckern, RSA benannt. Das RSA Kryptosystem weist mehrere Vorteile auf. Zum einen umgeht das RSA Verfahren das Schlüsselaustauschproblem, das bei symmetrischen Verschlüsselungsverfahren auftritt. Zum anderen gibt es keinen bekannten Algorithmus mit dem aus dem öffentlichen Schlüssel, der zum Verschlüsseln eingesetzt wird, der private Schlüssel, der zum Entschlüsseln verwendet wird, berechnet werden kann.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Eigenschaften
Das RSA Verfahren ist aufgrund folgender Eigenschaften als fast sicher einzustufen:
- Ein Klartextbuchstabe wird nicht immer auf den gleichen Geheimtextbuchstaben abgebildet. Es ist also nicht monoalphabetisch.
- Die RSA Verschlüsselung ist ein asymmetrisches Verfahren.
- Es gibt einen öffentlichen Schlüssel der zum Verschlüsseln eingesetzt wird und einen privaten Schlüssel, der zum Entschlüsseln verwendet wird. Das RSA Verfahren stellt unter anderem deshalb einen sicheren Verschlüsselungsalgorithmus dar, da aus dem öffentlichen Schlüssel nicht der private Schlüssel berechnet werden kann.
- Das RSA Verfahren eignet sich zur Kommunikation mit vielen Teilnehmern, da der öffentliche Schlüssel allen bekannt sein darf und somit nicht mit jedem Kommunikationsteilnehmer ein Schlüssel geheim ausgetauscht werden muss.
- Nur der Besitzer des privaten Schlüssels kann eine Nachricht wieder einfach entschlüsseln.
RSA Verschlüsselung einfach erklärt
Wie schon erwähnt, ist die RSA Verschlüsselung ein asymmetrisches Verschlüsselungsverfahren. Bei einem asymmetrischen Verfahren gibt es ein Schlüsselpaar aus einem öffentlichen und einem privaten Schlüssel. Der öffentliche Schlüssel wird zum Verschlüsseln eingesetzt und sollte für jeden frei zugänglich sein. Den privaten Schlüssel hingegen sollte nur der Besitzer kennen, da man nur mit diesem Schlüssel die Nachricht wieder entschlüsseln kann.
RSA Schlüssel
Im Folgenden zeigen wir dir, wie man sich beim RSA Kryptosystem ein Schlüsselpaar mit einem öffentlichen Schlüssel und einem privaten Schlüssel erzeugen kann. Zuerst wählt man sich zwei große Primzahlen  und
und  und berechnet anschließend die Produkte
und berechnet anschließend die Produkte


Hierbei ist  die Eulersche Phi-Funktion. Daraufhin sucht man sich eine Zahl
die Eulersche Phi-Funktion. Daraufhin sucht man sich eine Zahl  die teilerfremd zu
die teilerfremd zu  ist, sodass der größte gemeinsame Teiler von
ist, sodass der größte gemeinsame Teiler von  und
und  eins ist:
eins ist:

Wenn man ein solches  wählt, dann ist
wählt, dann ist  in
in  invertierbar. Somit kann man ein zu
invertierbar. Somit kann man ein zu  inverses Element
inverses Element  mit folgender Formel berechnen:
mit folgender Formel berechnen:

Damit hat man nun einen öffentlichen Schlüssel  , den man für jeden frei zugänglich macht und einen privaten Schlüssel
, den man für jeden frei zugänglich macht und einen privaten Schlüssel  , den man nur selbst kennen sollte.
, den man nur selbst kennen sollte.
RSA verschlüsseln
Um mit dem RSA Verfahren eine Nachricht verschlüsseln zu können, muss eine aus Buchstaben bestehende Nachricht zuerst in natürliche Zahlen umgewandelt werden. Hierfür wird oft der ASCII Code verwendet. Im Folgenden gehen wir davon aus, dass Bob an Alice eine geheime Nachricht senden möchte. Alice habe sich hierfür ein Schlüsselpaar mit dem öffentlichen Schlüssel  und einem privaten Schlüssel
und einem privaten Schlüssel  erzeugt.
erzeugt.
RSA berechnen – Verschlüsselung
Sei nun  , die Nachricht, die Bob an Alice senden möchte. Diese Nachricht verschlüsselt Bob mit Hilfe des öffentlichen Schlüssels
, die Nachricht, die Bob an Alice senden möchte. Diese Nachricht verschlüsselt Bob mit Hilfe des öffentlichen Schlüssels  von Alice, indem er
von Alice, indem er

berechnet, wobei  . Nachdem er
. Nachdem er  berechnet hat, verschickt er
berechnet hat, verschickt er  an Alice.
an Alice.
RSA entschlüsseln
Damit nun Alice die Nachricht von Bob entschlüsseln kann, benötigt sie eine Zusatzinformation, die der private Schlüssel enthält. Eine Funktion, die in eine Richtung leicht zu berechnen, aber sehr schwer umzukehren ist, nennt man eine Einwegfunktion. Gibt es jedoch eine Zusatzinformation, mit der die Umkehrung leicht durchgeführt werden kann, so spricht man von einer Falltürfunktion. Bei der RSA Verschlüsselung besitzt Alice gerade eine solche Zusatzinformation, mit Hilfe der die Funktion einfach umgekehrt werden kann.
RSA berechnen Entschlüsselung
Alice hat nun die Nachricht  erhalten und möchte diese Nachricht entschlüsseln, um herauszufinden, was Bob ihr mitteilen möchte. Hierfür berechnet sie
erhalten und möchte diese Nachricht entschlüsseln, um herauszufinden, was Bob ihr mitteilen möchte. Hierfür berechnet sie

in  . Wie oben schon erwähnt, gilt
. Wie oben schon erwähnt, gilt


Mit einer Verallgemeinerung des kleinen Satzes von Fermat, kann man nun  berechnen. Sei
berechnen. Sei

mit einem  . Hiermit gilt, dass
. Hiermit gilt, dass  für alle
für alle  . Deshalb ist insbesondere
. Deshalb ist insbesondere

Mit diesem Wissen kann Alice nun den Klartext  berechnen:
berechnen:

Definiert man sich  , dann erhält man durch einfaches Einsetzen und unter Verwendung der Verallgemeinerung des kleinen Satzes von Fermat den Klartext
, dann erhält man durch einfaches Einsetzen und unter Verwendung der Verallgemeinerung des kleinen Satzes von Fermat den Klartext 

Alice kann somit den Klartext lesen und weiß nun, was Bob ihr mitteilen möchte.
RSA Signatur
Mit Hilfe des RSA Verschlüsselungsverfahrens ist es auch möglich eine digitale Signatur zu erstellen. Eine digitale Signatur wird verwendet, um die Authentizität des Absenders zu überprüfen. Hierbei wird das Prinzip der Chiffrierung und Dechiffrierung umgedreht. Das heißt, der Absender einer Nachricht erstellt eine digitale Signatur unter Verwendung seines privaten Schlüssels und der Empfänger kann dann mit dem öffentlichen Schlüssel des Absender überprüfen, ob der Absender mit der digitalen Unterschrift übereinstimmt.
Man unterscheidet zwischen einer universellen Unterschrift und einer nicht universellen Unterschrift. Bei der universellen Unterschrift, wird wie schon beschrieben mit dem privaten Schlüssel eine digitale Signatur erstellt und an die zu übertragende Nachricht angehängt. Jeder der die Nachricht empfängt, also auch ein Dritter, der eventuell den Kommunikationskanal abhört, kann die Unterschrift mit dem öffentlichen Schlüssel des Senders überprüfen. Dies stellt jedoch meistens kein Problem dar, da die Unterschrift im Allgemeinen nicht geheim gehalten werden muss, da sie gerade dafür da ist, um die Authentizität des Senders zu überprüfen. Im Gegensatz zur universellen Unterschrift, wird bei der nicht universellen Unterschrift die digitale Signatur des Senders noch zusätzlich mit dem öffentlichen Schlüssel des Empfängers verschlüsselt, sodass nur der Empfänger die Authentizität des Senders überprüfen kann und nicht ein Dritter, der den Kommunikationskanal abhört.
RSA Verschlüsselung Beispiel
Im Folgenden werden wir uns an einem konkreten Beispiel anschauen, wie man einen Schlüssel erzeugt, und wie anschließend Nachrichten ausgetauscht werden können.
Gehen wir wieder von Alice und Bob aus. Damit sie Nachrichten austauschen können, muss jeder von ihnen ein Schlüsselpaar aus einem öffentlichen und einem privaten Schlüssel erzeugen.
Zuerst schauen wir uns an, wie Alice ein Schlüsselpaar generiert. Gehen wir davon aus, dass Alice die Primzahlen  und
und  wählt, dann kann Alice
wählt, dann kann Alice  und
und  berechnen
berechnen


Anschließend kann sie  und
und  mit folgender Formel bestimmen
mit folgender Formel bestimmen


Wählt Alice zum Beispiel  , so folgt
, so folgt  . Der öffentliche Schlüssel von Alice ist also
. Der öffentliche Schlüssel von Alice ist also  und der private Schlüssel ist
und der private Schlüssel ist  . Nun besitzt Alice ein Schlüsselpaar und ist mit der Schlüsselgenerierung fertig.
. Nun besitzt Alice ein Schlüsselpaar und ist mit der Schlüsselgenerierung fertig.
Analog erzeugt sich Bob ein Schlüsselpaar. Angenommen, Bob wählt die Primzahlen 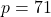 und
und  . Dann erhält er hiermit
. Dann erhält er hiermit


Damit kann er nun  und
und  bestimmen mit
bestimmen mit

Wählt Bob  , dann erhält er
, dann erhält er  . Damit ist Bob fertig mit der Schlüsselerzeugung. Er besitzt nun ein Schlüsselpaar aus dem öffentlichen Schlüssel
. Damit ist Bob fertig mit der Schlüsselerzeugung. Er besitzt nun ein Schlüsselpaar aus dem öffentlichen Schlüssel  und dem privaten Schlüssel
und dem privaten Schlüssel 
Gehen wir davon aus, dass Alice nun Bob die Nachricht „super“, senden möchte. Dann müssen die Buchstaben zuerst in Zahlen umgewandelt werden. Hierfür werde folgende Tabelle verwendet:
Tabelle folgt…
Wenn man das Wort „super“ mit dieser Tabelle in Zahlen ausdrückt, erhält man „super“  „19 21 16 05 18“. Um dies verschlüsseln zu können, benötigt Alice den öffentlichen Schlüssel von Bob. Diesen findet sie zum Beispiel frei zugänglich im Internet
„19 21 16 05 18“. Um dies verschlüsseln zu können, benötigt Alice den öffentlichen Schlüssel von Bob. Diesen findet sie zum Beispiel frei zugänglich im Internet  . Zum Verschlüsseln werden diese Zahlen nun in Blöcke der Länge vier geschrieben, sodass man folgende Blöcke erhält „1921 1605 1800“.
. Zum Verschlüsseln werden diese Zahlen nun in Blöcke der Länge vier geschrieben, sodass man folgende Blöcke erhält „1921 1605 1800“.
Anschließend verschlüsselt Alice jeden Block mit

in  , sie erhält
, sie erhält



Daraufhin sendet Alice die Nachricht „1172 5791 3536“ an Bob und Bob entschlüsselt diese Nachricht mit

Er erhält mit seinem privaten Schlüssel 



Splittet Bob nun die vierer Blöcke „1921 1605 1800“ wieder in zweier Blöcke „19 21 16 05 18 00“ auf und übersetzt die Zahlen nach der obigen Tabelle in Buchstaben, so erhält er die Nachricht von Alice im Klartext „super“.
RSA Verfahren – Sicherheit
Die Sicherheit des RSA Verfahrens basiert darauf, dass kein effizientes Verfahren existiert, das eine Zahl in ihre Primfaktoren zerlegt. Denn zum Entschlüsseln wird lediglich die Zahl  benötigt
benötigt

Um  berechnen zu können, benötigt man jedoch die Primfaktorzerlegung von
berechnen zu können, benötigt man jedoch die Primfaktorzerlegung von  , also
, also  und
und  oder
oder  . Zur heutigen Zeit (2019) existiert kein effizienter Algorithmus, mit dem dies möglich wäre. Deshalb stellt das RSA Verfahren heutzutage für große Primzahlen einen sicheren Verschlüsselungsalgorithmus dar.
. Zur heutigen Zeit (2019) existiert kein effizienter Algorithmus, mit dem dies möglich wäre. Deshalb stellt das RSA Verfahren heutzutage für große Primzahlen einen sicheren Verschlüsselungsalgorithmus dar.
RSA Verschlüsselung – Zusammenfassung
Zum Abschluss fassen wir nun die wichtigsten Eigenschaften des RSA Verfahrens zusammen.
Das RSA Verfahren ist ein asymmetrisches Verfahren, sodass das Schlüsselaustauschproblem, das bei symmetrischen Verfahren auftritt, umgangen wird. Außerdem können mit dem RSA Verfahren Integrität und Authentizität sichergestellt werden. Denn es gibt bis heute keinen effizienten Algorithmus, der eine Zahl in seine Primfaktoren zerlegen kann. Somit ist die Verschlüsselung mit dem RSA Verfahren sicher und es ist so gut wie nicht möglich eine mit dem RSA Verfahren erstellte digitale Signatur zu fälschen. Hört ein Angreifer eine RSA verschlüsselte Nachricht ab, so benötigt er sehr viel Rechenleistung und Zeit, um die RSA Verschlüsselung zu knacken.
Dies sind die Gründe, weshalb heutzutage häufig das RSA Verfahren bei der Datenübertragung im Internet eingesetzt wird. Würde es in der Zukunft jedoch gelingen, einen Algorithmus zu entwickeln, der eine Zahl effizient in ihre Primfaktoren zerlegen kann, so ist der RSA Algorithmus nicht mehr sicher. Eine weitere Gefahr für das RSA Verschlüsselungsverfahren stellt der Quantencomputer dar. Kommt jedoch ein solcher Computer auf den Markt, dann sind vermutlich alle bis heute bekannten Verschlüsselungsalgorithmen hinfällig, da dieser über eine gigantische Rechenleistung verfügt.