Vigenere Verschlüsselung
Die Vigenere Verschlüsselung wurde schon im 16. Jahrhundert benutzt, um Nachrichten verschlüsselt zu übertragen. Dabei verwendest du zum Verschlüsseln ein sogenanntes Schlüsselwort. In diesem Beitrag lernst du, wie die Vigenere Verschlüsselung funktioniert, was es mit dem Vigenere Quadrat auf sich hat und ob die Vigenere Chiffre heutzutage noch sicher ist.
Möchtest du alle wichtigen Informationen kurz und verständlich erklärt bekommen? Dann schau unser Video Vigenere Verschlüsselung dazu an!
Inhaltsübersicht
Vigenere Verschlüsselung Erklärung
Die Vigenere Verschlüsselung, auch Vigenere Chiffre genannt, ist ein polyalphabetisches Verschlüsselungsverfahren, das schon im 16. Jahrhundert verwendet wurde, um geheime Textnachrichten zu übermitteln. Im Gegensatz zur Caesar Verschlüsselung wird nicht das komplette Alphabet zyklisch verschoben, sondern es wird ein Schlüsselwort zum Verschlüsseln verwendet.
Vigenere Verfahren
Im Gegensatz zur Caesar Verschlüsselung wird bei dem Vigenere Verfahren nicht jeder Klartextbuchstabe um die gleiche Anzahl an Buchstaben verschoben. Stattdessen gibt es ein sogenanntes Schlüsselwort beziehungsweise Codewort. Den ersten Klartextbuchstaben verschlüsselt man dann mit dem ersten Buchstaben des Schlüsselwortes, den zweiten Buchstaben mit dem zweiten Buchstaben des Schlüsselwortes und so weiter. Ist das Schlüsselwort zu Ende, beginnt man wieder mit dem ersten Buchstaben. Weist man den Buchstaben Zahlen von 0-25 zu, so kann man aus dem Klartextbuchstaben den Geheimtextbuchstaben mit einer einfachen Addition berechnen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Vigenere Verschlüsselung Beispiel
Im Folgenden wird gezeigt, wie man mit der Vigenere Verschlüsselung den Satz „ich bin ein sicherer satz“ mit dem Schlüsselwort „sicher“ verschlüsseln kann. Hierfür schreibt man unter den zu verschlüsselnden Satz das Schlüsselwort:
| Klartext | i | c | h | b | i | n | e | i | n | s | i | c | h | e | r | e | r | s | a | t | z |
| Schlüssel | s | i | c | h | e | r | s | i | c | h | e | r | s | i | c | h | e | r | s | i | c |
Drückt man alle 26 Buchstaben des Alphabets mit Zahlen von 0-25 aus, so kann man den jeweiligen Geheimtextbuchstaben durch Addition in 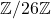 ermitteln. Hierfür werden die Buchstaben zuerst als Zahlen ausgedrückt und anschließend die Zahl eines Klartextbuchstabens mit der Zahl des dazugehörigen Schlüsselwortbuchstabens addiert. Berechnet man das Ergebnis in
ermitteln. Hierfür werden die Buchstaben zuerst als Zahlen ausgedrückt und anschließend die Zahl eines Klartextbuchstabens mit der Zahl des dazugehörigen Schlüsselwortbuchstabens addiert. Berechnet man das Ergebnis in 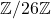 , lässt sich der zugehörige Geheimtextbuchstabe ermitteln.
, lässt sich der zugehörige Geheimtextbuchstabe ermitteln.
Für unser oben gewähltes Beispiel erhält man:
| Klartext | i | c | h | b | i | n | e | i | n | s | i | c | h | e | r | e | r | s | a | t | z |
| 8 | 2 | 7 | 1 | 8 | 13 | 4 | 8 | 13 | 18 | 8 | 2 | 7 | 4 | 17 | 4 | 17 | 18 | 0 | 19 | 25 | |
| Schlüssel | s | i | c | h | e | r | s | i | c | h | e | r | s | i | c | h | e | r | s | i | c |
| 18 | 8 | 2 | 7 | 4 | 17 | 18 | 8 | 2 | 7 | 4 | 17 | 18 | 8 | 2 | 7 | 4 | 17 | 18 | 8 | 2 | |
| Geheimtext | a | k | j | i | m | e | w | q | p | z | m | t | z | m | t | l | v | j | s | b | b |
| 0 | 10 | 9 | 8 | 12 | 4 | 22 | 16 | 15 | 25 | 12 | 19 | 25 | 12 | 19 | 11 | 21 | 9 | 18 | 1 | 1 |
Exemplarisch werden im Folgenden die Berechnungen für die ersten drei Buchstaben dargestellt:



Nach dem Verschlüsseln mit der Vigenere Verschlüsselung, erhält man also den Geheimtext „akjimewqpzmtzmtlvjsbb“.
Vigenere-Quadrat
Das Vigenere Quadrat stellt eine Alternative dar, mit dem man einen Klartext mit einem bestimmten Schlüsselwort verschlüsseln kann. Dabei muss man die Buchstaben nicht als Zahlen ausdrücken. Hierfür schreibt man ausgehend vom lateinischen Alphabet mit 26 Buchstaben alle Caesar Verschiebungen darunter. Zuerst die Caesar-Verschiebung um null Stellen, darunter die Caesar Verschiebung um eine Stelle und so weiter, bis zur Caesar Verschiebung um 25 Stellen. Somit erhält man ein Quadrat mit 26 x 26 Buchstaben. Dieses Quadrat wird Vigenere Quadrat genannt.
Im unten gezeigten Quadrat, stellt die abgegrenzte linke Spalte die Buchstaben im Klartext dar, und die abgegrenzte erste Zeile die Buchstaben des Schlüsselwortes. Möchte man nun einen Klartext in einen Geheimtext umwandeln, so bestimmt man den ersten Geheimtextbuchstaben, indem man die Zeile des Klartextbuchstabens und die Spalte des Schlüsselwortbuchstabens sich kreuzen lässt. Der Buchstabe, bei dem sich die jeweilige Zeile und Spalte kreuzen, ist dann der Geheimtextbuchstabe. Analog verfährt man mit den anderen Buchstaben des Klartextes.
Für das Wort „ich“ und das Schlüsselwort „sic“ erhält man dann die im unteren Quadrat rot markierten Buchstaben. Unter Verwendung dieses Quadrats kann man einen Klartext einfach verschlüsseln.
Vigenere Quadrat folgt…
Man erhält mit der Methode des Vigenere Quadrats denselben Geheimtext, wie mit der oberen Modulo Berechnung.
Vigenere Chiffre – Sicherheit
Die Sicherheit der Vigenere Chiffre beziehungsweise Vigenere Verschlüsselung hängt von der Länge des Schlüsselwortes und der Länge des zu verschlüsselnden Textes ab. Je länger der Text, desto größer ist die Wahrscheinlichkeit, dass sich Wörter wiederholen und daraus das Schlüsselwort berechnet werden kann. Umso länger das Schlüsselwort, desto sicherer ist die Verschlüsselung. Außerdem sollte man den Schlüssel zufällig wählen.
Vigenere entschlüsseln
Möchte man einen vigenère-verschlüsselten Text wieder entschlüsseln, dann ist dies einfach mit dem Schlüsselwort möglich. Dabei addiert man jedoch nicht das Schlüsselwort, wie dies bei der Verschlüsselung der Fall ist, sondern subtrahiert es vom Geheimtext und berechnet anschließend den Modulo.
Ist man jedoch nicht im Besitz des Schlüsselwortes, so gibt es verschiedene Kryptoanalysen, um dieses zu ermitteln. Zuerst versucht man normalerweise die Schlüssellänge herauszufinden. Hierfür eignet sich der Kasiski-Test. Man sucht im Geheimtext nach Buchstabenfolgen, die sich wiederholen. Über den Abstand zweier solcher Buchstabenfolgen, lässt sich dann meist die Schlüsselwortlänge ermitteln. Dabei zählt man den Abstand des ersten Buchstabens der ersten Folge bis zum ersten Buchstaben der zweiten Folge. Konnte man mit diesem Verfahren die Schlüsselwortlänge in Erfahrung bringen, dann kann man anschließend den Geheimtext in Blöcke mit der ermittelten Schlüssellänge aufteilen. Da nun der erste Buchstabe aller Blöcke immer mit dem gleichen Buchstaben verschlüsselt wurde, kann man nun eine Häufigkeitsanalyse durchführen und damit den Klartextbuchstaben ermitteln. Analog verfährt man mit den anderen Buchstaben.
Vigenere Verschlüsselung Java
Im Folgenden wird eine mögliche Implementierung der Vigenere Verschlüsselung in Java gezeigt:
import java.util.Scanner;
public class vigenere {
public static char[] crypt(char[] plain, char[] key, int direction) {
char[] output = new char[plain.length];
for (int i = 0; i < plain.length; i++) {
//Verschluesseln
if (direction == 1) {
//Umrechnen für ASCII Tabelle
int result = (plain[i] + key[i % key.length]-194) % 26 ;
output[i] = (char) (result+97);
}
//Entschluesseln
else if (direction == 0){
int result;
if (plain[i] - key[i % key.length] < 0)
{
result = (plain[i]- key[i % key.length]+130) %26 + 97;
}
else
{
result = (plain[i] - key[i % key.length]) % 26 +97;
}
output[i] = (char) result;
}
}
return output;
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
System.out.println("Klartext eingeben:");
String plaintext = scanner.nextLine(); //ohne Umlaute
plaintext = plaintext.toLowerCase();
char[] plain = plaintext.toCharArray();
System.out.println("Schluesselwort eingeben:");
String keyword = scanner.nextLine();
keyword = keyword.toLowerCase();
char[] key = keyword.toCharArray();
char[] encrypted = crypt(plain, key, 1);
System.out.println("Verschluesselter Text:");
System.out.println(encrypted);
char[] decrypted = crypt(encrypted, key, 0);
System.out.println("Entschluesselter Text:");
System.out.println(decrypted);
scanner.close();
}
}