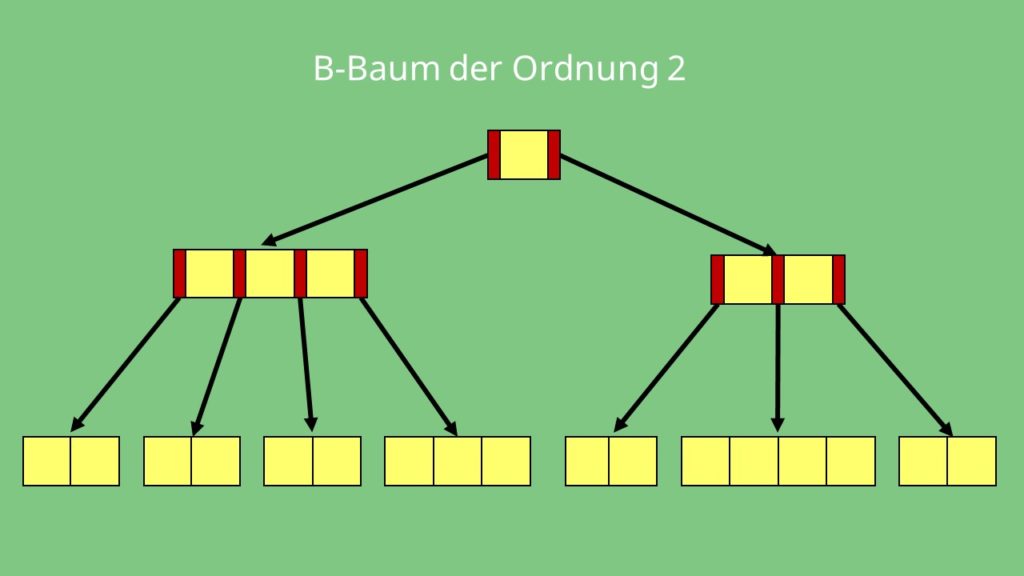
B-Baum
In diesem Artikel wird der B-Baum einfach erklärt. Hier findest du die allgemeine Definition der B-Baum Ordnung, sowie ein Beispiel von einem B-Baum der Ordnung 2. Zusätzlich zeigen wir dir, die verschiedenen Varianten der Operationen: Suchen, B-Baum Einfügen, B-Baum Löschen von Elementen eines Blatts, sowie eines inneren Knotens mittels Verschiebungen und Verschmelzungen inklusive Beispiel.
Doch eigentlich willst du die Funktionsweise einfach und schnell an einem B-Baum Beispiel verstehen? Kein Problem! In unserem Video zeigen wir dir schnell die verschiedenen Operationen!
Inhaltsübersicht
B-Baum Allgemein
Ein B-Baum ist eine Datenstruktur in der Informatik, die sich vor allem für Datenbanken und Dateisysteme eignet. Dabei handelt es sich um keinen Binärbaum , sondern um einen vollständig balancierten Baum, welcher in einem Knoten mehrere Elemente sortiert speichern kann.
B-Bäume Geschichte
1972 wurden die B-Bäume (Englisch B-tree) von Rudolf Bayer und Edward M. McCreight entwickelt. In Kombination mit dem relationalen Datenbankmodell wurde die erste Basis für SQL-Datenbanksysteme bei IBM geschaffen, da der Baum eine perfekte Daten- und Indexstruktur zur Verwaltung von Indizes darstellt.
Schlüssel.
Schlüssel.
Schlüsseln hat immer 
Söhne.
B-Baum einfach erklärt
Nun der B-Baum einfach erklärt! B-Bäume gehören zu den balancierten Bäumen, die Daten sortiert speichern. Im Gegensatz zu den meisten anderen Bäumen werden Elemente hier zunächst in den Blättern eingefügt. B-Bäume wachsen damit nach oben von den Blättern zur Wurzel. B-Bäume sind auf die Ablage in Sekundärspeichern optimiert und daher von großer praktischer Relevanz.
In den Knoten eines B-Baumes ist eine variable Anzahl von Schlüsseln gespeichert. Diese ist in jedem Fall nach oben begrenzt und oft auch nach unten. Eine häufig verwendete Begrenzung ist zum Beispiel „2 4“. In einem solchen Baum müssen in den Knoten mindestens 2 Elemente und dürfen maximal 4 Elemente gespeichert werden. Die Schlüssel sind dabei aufsteigend sortiert.
Darüber hinaus werden noch „Anzahl Knoten +1“ Verweise auf Kindknoten gespeichert. Ein Verweis zwischen zwei Elementen eines Knotens zeigt dann auf einen Bereich, der nur Elemente enthält, die zwischen diesen Elementen des Elternknotens liegen.
Die maximale Anzahl an Verweisen eines Knotens ist als Verzweigungsgrad oder Ordnung bekannt. Entsprechend darf ein Knoten dann höchstens Verzweigungsgrad – 1 Elemente speichern.
Achtung! Wie es in der Informatik oftmals der Fall ist, so ist diese Definition nicht allgemeingültig. Manchmal wird als Ordnung auch die maximale Anzahl an Elementen pro Knoten definiert.
Maximale Höhe
B-Baum der Ordnung m mit n Schlüsseln:
Eine 
hat 
Knoten.
Dabei teilt man den Wertebereich der Schlüssel in 
Intervalle ein:
Daraus folgt wiederum:
Die Höhe muss immer eine ganze Zahl sein, deshalb gilt:
Suchen
- Startpunkt der Suche ist der Wurzelknoten mit der Überprüfung auf den gesuchten Wert.
- Findet man den gesuchten Wert nicht in der Wurzel, wird mittels des jeweiligen Verweises zum nächsten Knoten rekursiv fortgefahren und damit die inneren Knoten überprüft.
- Wird der Wert in den inneren Knoten nicht gefunden, werden im letzten Schritt die Blätter untersucht. Liegt der Wert auch dort nicht vor, ist er nicht im Baum gespeichert.
Komplexität
- Maximale Anzahl von Zugriffen auf den Hintergrundspeicher:
- Suche innerhalb eines Knotens:
- Gesamtlaufzeit:
B-Baum Einfügen
Wenn man in einen B-Baum einfügen möchte, wird erstmal das entsprechende Blatt gesucht, in dem das neue Element eingefügt werden soll.
Nun muss zwischen zwei Fällen unterschieden werden:
-
Die Anzahl der Einträge des Knotens ist nach dem Einfügen noch kleiner
: Das bedeutet, dass der Knoten seine maximale Anzahl an Elementen nach dem Einfügen nicht überschritten hat. Deshalb kann der neue Wert ohne Probleme an seine richtige Position eingefügt werden und die Operation ist damit beendet. -
Die Anzahl der Einträge des Knotens ist nach dem Einfügen größer gleich : Die Anzahl der maximalen Elemente wurde überstiegen. Deshalb muss er im weiteren Verlauf aufteilt werden, um ihn in den darüber liegenden Knoten einzufügen. Deshalb sagt man auch, dass ein B-Baum nach oben wächst!
B-Baum Einfügen Beispiel
Als Beispiel dient der folgende Baum der Ordnung 4 mit den bestehenden Werten 20, 50 und 70. Hier soll nun die Zahl 35 einfügt werden. Die 35 ist größer als die 20 aber kleiner als die 50, deswegen wird der neue Wert dazwischen eingefügt.
Der Knoten überschreitet damit die Ordnung und wird deshalb nächsten Schritt aufgeteilt. Hierfür nimmt man das mittlere Element, in unserem Fall die 35 oder die 50, und fügt es in den darüber liegenden Knoten ein. Da kein darüberliegender Knoten existiert, wird ganz einfach ein Neuer erstellt! Jetzt müssen nur noch die Kanten für die Verbindung zwischen den Kindknoten und dem neuen Knoten gesetzt werden. Damit ist die Einfüge-Operation abgeschlossen.
B-Baum Löschen
Das B-Baum Löschen stellt sich deutlich komplexer dar. Die allgemeine Unterscheidung der Durchführung einer Lösch-Operation lässt sich in drei Fällen beschreiben:
Die Anzahl der Elemente bzw. Einträge eines Knotens, aus dem der gewünschte Wert gelöscht werden soll, ist immer noch entsprechend der Ordnung.
Der Knoten besitzt nach dem Löschen zu wenig Einträge.
Das Blatt besitzt nach dem Löschen zu wenig Elemente.
Die verschiedenen Vorgehensweisen, werden im folgenden Kapitel „B-Baum Löschen Beispiel“ genauer erläutert.
Verschiebung
Im nächsten Schritt löscht man die 40. In diesem Fall hätte der mittlere Knoten zu wenige Elemente. Deshalb muss jetzt mittels Verschiebung gelöscht werden. Da der rechte Nachbarknoten ausreichend Elemente hat, kann er deshalb sein kleinstes Element nach oben abgeben. Jetzt kann das Element, das direkt neben dem gerade verschobenen Element liegt, in unseren mittleren Knoten einfügt werden. Damit sind alle unsere Bedingungen erfüllt!
Verschmelzung
Neben der Verschiebung gibt es noch eine weitere Methode einen Löschvorgang richtig durchzuführen – die Verschmelzung. Die Verschmelzung wird benötigt, wenn kein Knoten Elemente abgegeben kann.
In diesem Beispiel ist das der Fall, wenn die 50 gelöscht werden soll. Hierfür muss das Element des Elternknotens, das zwischen den zu verschmelzenden Knoten liegt, sich in den neuen Knoten ziehen. Damit kann dann der Knoten zusammenfasst bzw. verschmolzen werden.
Innerer Knoten
Etwas ist komplizierter, wenn Elemente aus einem inneren Knoten gelöscht werden.
Zu besseren Veranschaulichung dient zu diesem Zweck nun ein neues Beispiel. Aus diesem Baum mit minimalem Verzweigungsgrad 3 möchte man die Zahl 20 löschen. Um die Bedingung der Mindestanzahl im Knoten zu erhalten, muss ein Element aus einem Kindknoten das zu löschende Element ersetzen. Dafür eignet sich nur der mittlere Kindknoten, weil er aus drei Elementen besteht.
Dabei gilt die allgemeine Regel:
Beim Nutzen des linken Nachfolgers benötigt man dessen größtes Element. Andersrum benutzt man natürlich beim rechten Nachfolger dessen kleinstes Element!
Der Mittlere Knoten ist der linke Nachfolger der 20, also zieht man das größte Element – die 17 – nach oben.
Weitere Varianten
B-Bäume können in weiteren Varianten und Spezialfällen auftreten:
- B+ Baum
- B* Baum
- 2-3-4 Baum
- AVL-Baum
- Rot-Schwarz-Baum
- R-Baum
B+ Baum
Der B+ Baum stellt eine Variante des B-Baums dar. Dabei enthalten die inneren Knoten nur Schlüssel und die eigentlichen Daten werden nur in Blattknoten gespeichert. Linke Kindknoten sind hier echt kleiner als das rechte Elternelement und rechte größer gleich. Die Zugriffszeit auf ein Datenelement verbessert sich durch diese Variation.
B* Baum
Der B* Baum stellt eine weitere Erweiterung des B-Baums mit einem Mindestfüllgrad von 2/3 durch eine veränderte Split-Strategie. Dabei werden 2 volle Knoten auf 3 Knoten mit einer 2/3-Füllung aufgeteilt, anstatt bei einem Überlauf direkt einen weiteren Knoten anzulegen.