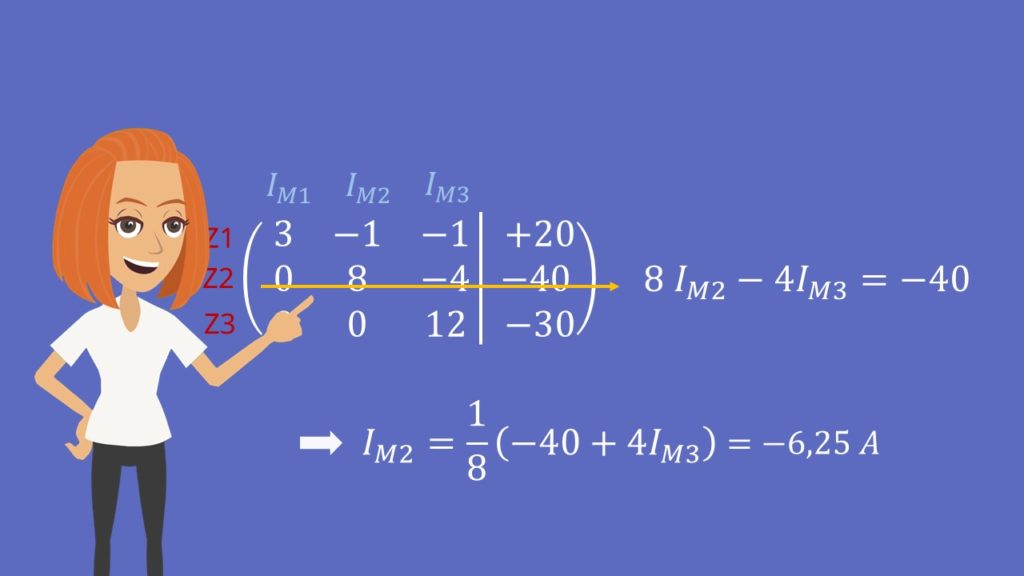Gaußsches Eliminationsverfahren
In diesem Beitrag zeigen wir dir, wie du mithilfe des Gaußschen Eliminationsverfahrens lineare Gleichungssysteme schnell lösen kannst.
Schau auch gleich in unser Video dazu rein, in dem du das Verfahren Schritt für Schritt nachverfolgen kannst.
Inhaltsübersicht
Gaußsches Eliminationsverfahren einfach erklärt
Das Gaußsche Eliminationsverfahren ist ein Verfahren zur Lösung linearer Gleichungssysteme. Dafür wird das Gleichungssystem zunächst in Matrixform ausgedrückt. Anschließend formst du die Matrix, durch Zeilenumformung so um, dass ihre Werte unterhalb der Hauptdiagonalen zu 0 werden. In der untersten Zeile kannst du nun die Lösung der ersten Unbekannten ermitteln. Diese Lösung setzt du dann in die Zeile darüber ein um deine nächste Unbekannte zu bestimmen. Diesen Vorgang wiederholst du solange, bis du alle Unbekannten bestimmt hast und damit dein Gleichungssystem gelöst ist.
Anwendung des Gaußschen Eliminationsverfahrens
Bei der Analyse von elektronischen Schaltungen mit dem Maschenstrom – oder Knotenpunktpotentialverfahren erhalten wir ein Gleichungssystem, das sich als Matrixgleichung schreiben lässt. Allgemein kann das so aussehen:
Matrix-Gleichungen können mithilfe verschiedener Verfahren gelöst werden: Eine Möglichkeit ist die Cramersche Regel . Die Alternative dazu ist das Gaußsche Eliminationsverfahren, welches wir dir hier vorstellen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Umwandlung des Gleichungssystems
Beginnen wir mit Schritt eins des Gaußschen Eliminationsverfahrens, der Umwandlung des Gleichungssystems. Dazu multiplizieren wir jedes Element des Vektors mit jedem Element der jeweiligen Zeile der Matrix. Der Ergebnisvektor wird dann durch einen Strich vom Rest der Matrix getrennt. Diese Form der Matrix benötigen wir, um danach weiterrechnen zu können.
Der Vektor mit den gesuchten Strömen steht nun über den einzelnen Spalten. Wir schreiben ihn dabei aber nicht hin, sondern behalten ihn einfach im Kopf. Zudem nummerieren wir die einzelnen Zeilen durch.
Matrix in Stufenform
Schritt zwei ist dann die Matrixumformung in Stufenform, sodass nur auf und oberhalb der Diagonalen Werte ungleich Null stehen. Das erreichst du durch geschicktes multiplizieren und späterem Addieren bzw. Subtrahieren der Zeilen.
Im Folgenden demonstrieren wir die die Anwendung des Gaußschen Eliminationsverfahrens an einem Beispiel.
Gaußsches Eliminationsverfahren Beispiel
Gesucht sind die Maschenströme  ,
,  und
und  . Alle Widerstände sind gleich groß und haben den Wert
. Alle Widerstände sind gleich groß und haben den Wert  . Die Spannungsquelle
. Die Spannungsquelle  hat
hat  Volt und die Quelle
Volt und die Quelle  liefert
liefert  Volt. Nun können wir die Werte einsetzen. Die Matrix sieht jetzt so aus:
Volt. Nun können wir die Werte einsetzen. Die Matrix sieht jetzt so aus:
Für die weiteren Rechnungen vernachlässigen wir die Einheiten – wir schauen uns also nur die Zahlen an.
An dieser Stelle können wir das Gaußsche Eliminationsverfahren anwenden.
Dabei eliminierst du als erstes die beiden unteren Plätze deiner Matrix. Dafür multiplizieren wir alle Werte der zweiten und dritten Zeile mit dem Faktor drei.
Jetzt haben wir auf den beiden zu eliminierenden Stellen  stehen. Wenn wir jetzt die erste Zeile addieren, kommen wir auf die gewünschte Null.
stehen. Wenn wir jetzt die erste Zeile addieren, kommen wir auf die gewünschte Null.
Wenn du sicher im Rechnen bist, dann kannst du das ganze natürlich auch in einem Schritt machen. Neben dem Pfeil steht dann:  wird zu
wird zu  mal
mal  plus
plus  und
und  wird zu
wird zu  mal
mal  plus
plus  .
.
Um die berühmte Treppe aus lauter Nullen zu erhalten, braucht die letzte Reihe eine weitere Null. Hierfür multiplizieren wir die dritte Zeile mit dem Faktor 2, um anschließend durch das Addieren der zweiten Zeile auf Null zu kommen.
Auflösen des Gleichungssystems
Wir haben das Ziel des Gaußschen Eliminationsverfahrens erreicht – das Ergebnis ist die Matrix in Stufenform. Hier noch ein Tipp: Schreibe dir bei deiner Matrixumformung am besten jeden deiner Rechenschritte Schritt für Schritt auf. Denn wenn du dich verrechnen solltest, dann hilft das ungemein bei der Fehlersuche.
Kommen wir jetzt zu Schritt drei, dem rekursiven Auflösen. Das heißt, dass immer wieder in das Ergebnis in die Zeile darüber eingesetzt wird. Rekursiv bedeutet dabei, dass wir in der letzten Zeile anfangen, denn in dieser steht schon „fast“ das Ergebnis für den Maschenstrom  . Wir erinnern uns an die Bedeutung der einzelnen Spalten: Spalte 1 steht für
. Wir erinnern uns an die Bedeutung der einzelnen Spalten: Spalte 1 steht für  , Spalte 2 für
, Spalte 2 für  und Spalte 3 für
und Spalte 3 für  .
.
Jetzt schreibst du die Gleichungen der einzelnen Zeilen heraus.
In Zeile 3 steht:

 ist also
ist also  durch
durch  und das ist
und das ist  . Dabei darfst du natürlich die Einheit Ampere nicht vergessen.
. Dabei darfst du natürlich die Einheit Ampere nicht vergessen.
In Zeile 2 steht:

Umgeformt auf  ergibt das: Ein Achtel mal Minus
ergibt das: Ein Achtel mal Minus  plus vier
plus vier  .
.  haben wir ja gerade eben berechnet.
haben wir ja gerade eben berechnet.  ist also -6,25 Ampere.
ist also -6,25 Ampere.
Zuletzt löst du noch Zeile 1 auf.
In Zeile 1 steht

Auflösen nach  und einsetzen der gerade eben berechneten anderen Ströme bringt dich zur Lösung:
und einsetzen der gerade eben berechneten anderen Ströme bringt dich zur Lösung:

Eigentliche Richtung des Maschenstromes
Das war es auch schon. Das Ergebnis für die einzelnen Ströme ist das gleiche wie beim Beitrag zur Cramerschen Regel. Das bedeutet, erstens, dass wir uns nicht verrechnet haben und zweitens, dass beide Verfahren trotz verschiedener Vorgehensweisen zur Lösung führen.
Wir haben nun die Maschenströme mit der Annahme berechnet, dass alle Widerstände gleich groß sind und die Spannungsquellen 5V beziehungsweise 20V liefern. Der Maschenströme IM3 und IM2 sind negativ. Das bedeutet, dass die durch den Maschenumlauf angenommene Richtung des Maschenstromes falsch war – in Wirklichkeit fließt der Strom nämlich in die andere Richtung. Das erkennst du an dem negativen Vorzeichen.
Mit diesem Fahrplan kannst du das Gaußsche Eliminationsverfahren Schritt für Schritt einfach anwenden. Probiere es gleich aus!