abc Formel
Du willst wissen, was es mit der abc-Formel auf sich hat? Dann bist du bei unserem Video und Beitrag genau richtig!
Inhaltsübersicht
abc-Formel — Anwendung
Möchtest du Gleichungen oder die Nullstellen einer quadratischen Funktion mithilfe der abc-Formel ausrechnen, kannst du unsere Schritt-für-Schritt-Anleitung befolgen.
➡️ Beispiel 1: 2x2 – 16 = 4x
- Schritt 1: Gleichung gleich 0 setzen. Um die abc-Formel anzuwenden, muss auf einer Seite der Gleichung die Null stehen. Ggf. musst du die Gleichung umstellen.
2x2 – 16 = 4x | – 4x
2x2 – 16 – 4x = 0
2x2 – 4x – 16 = 0
- Schritt 2: Koeffizienten a, b und c ablesen
ax2 + bx + c = 0
2x2 – 4x – 16 = 0
a = 2, b = -4, c = -16
- Schritt 3: a, b und c in die Formel einsetzen


- Schritt 4: Ergebnisse ausrechnen

 und
und 
- Schritt 5: Nullstellen aufschreiben
x1 = 4
x2 = -2
➡️ Beispiel 2: f(x) = x2 + 4x + 4
- Schritt 1: Gleichung gleich 0 setzen
x2 + 4x + 4 = 0
- Schritt 2: a, b und c ablesen
a = 1, b = 4, c = 4
- Schritt 3: a, b und c in die Formel einsetzen


- Schritt 4: Ergebnisse ausrechnen

 und
und 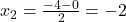
- Schritt 5: Nullstellen aufschreiben
x1 = -2
x2 = -2
Die Funktion hat bei x= -2 eine doppelte Nullstelle.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
abc-Formel — Diskriminante
Mithilfe der abc-Formel kannst du erkennen, ob eine quadratische Gleichung eine, zwei oder keine Lösung hat. Dafür verwendest du den Teil unter der Wurzel b² – 4ac. Den bezeichnest du auch als Diskriminante D.
-
D > 0: Die quadratische Gleichung hat zwei Lösungen
➡️ Beispiel: x² – 5x + 6 = 0
Diskriminante D = (-5)² – 4 ⋅ 1 ⋅ 6 = 25 – 24 = 1
→ x1 = 3; x2 = 2
-
D = 0: Die quadratische Gleichung hat eine Lösung
➡️ Beispiel: x² – 4x + 4 = 0
Diskriminante D = (-4)² – 4 ⋅ 1 ⋅ 4 = 16 – 16 = 0
→ x1/2 = 8
-
D < 0: Die quadratische Gleichung hat keine Lösung
➡️ Beispiel: x² + 2x + 5 = 0
Diskriminante D = 2² – 4 ⋅ 1 ⋅ 5 = 4 – 20 = -16
→ kein Ergebnis für x1/2 möglich
abc-Formel — Herleitung
Abschließend zeigen wir dir, wie du die abc-Formel herleiten kannst. Dabei musst du die allgemeine Gleichung ax² + bx + c = 0 nach x auflösen. Dafür benötigst du die quadratische Ergänzung und die erste binomische Formel .

abc Formel — häufigste Fragen
(ausklappen)
abc Formel — häufigste Fragen
(ausklappen)-
Wann kann ich die abc-Formel überhaupt benutzen?Du kannst die abc-Formel benutzen, wenn du eine quadratische Gleichung der Form
 lösen willst. Sie eignet sich auch, um Nullstellen einer quadratischen Funktion
lösen willst. Sie eignet sich auch, um Nullstellen einer quadratischen Funktion  zu bestimmen. Wichtig ist, dass die Gleichung auf 0 gesetzt ist.
zu bestimmen. Wichtig ist, dass die Gleichung auf 0 gesetzt ist.
-
Wie mache ich aus einer Gleichung zuerst die Form ax² + bx + c = 0?Du bringst alle Terme auf eine Seite, sodass auf der anderen Seite 0 steht. Dafür addierst oder subtrahierst du passende Terme auf beiden Seiten, bis die Gleichung die Form
 hat. Zum Beispiel wird aus
hat. Zum Beispiel wird aus  die Form
die Form  .
.
-
Wie lese ich a, b und c richtig ab, wenn vor x kein Plus steht?Du liest a, b und c immer mit Vorzeichen ab, auch wenn kein Plus dasteht. Ein Minus vor einem Term gehört also zum Koeffizienten. In
 gilt deshalb
gilt deshalb  ,
,  und
und  .
.
-
Was sagt mir die Diskriminante D darüber, wie viele Lösungen es gibt?Die Diskriminante
 zeigt dir, ob es zwei, eine oder keine Lösung gibt. Gilt
zeigt dir, ob es zwei, eine oder keine Lösung gibt. Gilt  , hat die Gleichung zwei Lösungen, bei
, hat die Gleichung zwei Lösungen, bei  genau eine Lösung und bei
genau eine Lösung und bei  keine Lösung. Der Wert D steht unter der Wurzel.
keine Lösung. Der Wert D steht unter der Wurzel.
-
Wie erkenne ich an meinen Ergebnissen, ob ich eine doppelte Nullstelle habe?Du erkennst eine doppelte Nullstelle daran, dass beide Lösungen gleich sind, also
 . Dann liefert die abc-Formel zweimal denselben Wert, weil unter der Wurzel 0 steht. Zum Beispiel ergibt
. Dann liefert die abc-Formel zweimal denselben Wert, weil unter der Wurzel 0 steht. Zum Beispiel ergibt  die Lösungen
die Lösungen  und
und  .
.
pq-Formel
Neben der abc-Formel kannst du zum Lösen von quadratischen Gleichungen auch die pq-Formel verwenden. Welche Formel das ist und wie du sie anwendest, zeigen wir dir in unserem Video!
![Rendered by QuickLaTeX.com \[ x_{1,2} = \cfrac{-\textcolor{blue}{b} \pm \sqrt{\textcolor{blue}{b}^2-4\textcolor{red}{a}\textcolor{olive}{c}}}{2\textcolor{red}{a}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4840e3a8c69824aabc16ad48a06db5ae_l3.png)
