Schiefer Wurf
Der schiefe Wurf beschreibt viele Systeme der klassischen Mechanik , angefangen beim einfachen Beispiel eines geworfenen Balls. Wenn du also schon immer einmal durchrechnen wolltest, wie weit du beim Werfen kommst – hier erfährst du alles, was du dafür brauchst!
In unserem Video zum schiefen Wurf kannst du das alles übrigens noch bequemer und schneller lernen. Schau doch mal rein!
Inhaltsübersicht
Schiefer Wurf einfach erklärt
Der schiefe Wurf oder auch schräge Wurf beschreibt ein physikalisches System, bei dem ein Körper „schräg nach oben und nach vorne geworfen“ wird – seine Anfangsgeschwindigkeit bildet also einen Winkel mit der Horizontalen – und dann unter dem Einfluss der konstanten Erdbeschleunigung nach unten fällt.
Vernachlässigt man die Luftreibung, so ist die Flugbahn, auch Bahnkurve genannt, des Körpers parabelförmig. Wird der Luftwiderstand berücksichtigt, so ergibt sich aus der bisherigen Wurfparabel die realistischere ballistische Kurve.
Schiefer Wurf Formeln
Die Bewegung beim schrägen Wurf ergibt sich durch das Superpositionsprinzip
(ungestörte Überlagerung) der Bewegungen in horizontaler  -Richtung und vertikaler
-Richtung und vertikaler  -Richtung. Dabei haben wir in
-Richtung. Dabei haben wir in  -Richtung eine gleichförmige Bewegung mit der konstanten (Anfangs-)Geschwindigkeit
-Richtung eine gleichförmige Bewegung mit der konstanten (Anfangs-)Geschwindigkeit  und und in
und und in  -Richtung eine beschleunigte Bewegung mit der Anfangsgeschwindigkeit
-Richtung eine beschleunigte Bewegung mit der Anfangsgeschwindigkeit 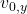 und der konstanten Erdbeschleunigung
und der konstanten Erdbeschleunigung  nach unten.
nach unten.
Die gesamte Anfangsgeschwindigkeit  können wir in die Komponenten in
können wir in die Komponenten in  – und
– und  -Richtung zerlegen
-Richtung zerlegen

mit  dem Winkel der Anfangsgeschwindigkeit zur Horizontalen. Dem Anfangsort, also dem Startpunkt des Wurfes, geben wir die Koordinaten
dem Winkel der Anfangsgeschwindigkeit zur Horizontalen. Dem Anfangsort, also dem Startpunkt des Wurfes, geben wir die Koordinaten  und
und  . Zudem wählen wir die Anfangsgeschwindigkeiten positiv:
. Zudem wählen wir die Anfangsgeschwindigkeiten positiv:  .
.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Zeit-Ort-Gesetz
Mit den zeitabhängigen  – und
– und  -Koordinaten des Körpers beschreiben wir seine Flugbahn beim schiefen Wurf. Für diese Koordinaten finden wir das folgende „Zeit-Ort-Gesetz“
-Koordinaten des Körpers beschreiben wir seine Flugbahn beim schiefen Wurf. Für diese Koordinaten finden wir das folgende „Zeit-Ort-Gesetz“
 .
.
Wir sehen, dass die Bewegung in  -Richtung nur linear in der Zeit
-Richtung nur linear in der Zeit  ist. Sie verläuft also mit der konstanten Geschwindigkeit
ist. Sie verläuft also mit der konstanten Geschwindigkeit  . Das ergibt Sinn, denn in
. Das ergibt Sinn, denn in  -Richtung wirkt keine Beschleunigung. In
-Richtung wirkt keine Beschleunigung. In  -Richtung hingegen starten wir zwar mit der Anfangsgeschwindigkeit
-Richtung hingegen starten wir zwar mit der Anfangsgeschwindigkeit 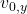 , es wirkt aber die konstante Erdbeschleunigung
, es wirkt aber die konstante Erdbeschleunigung  nach unten und die beschleunigte Bewegung ist quadratisch in der Zeit.
nach unten und die beschleunigte Bewegung ist quadratisch in der Zeit.
Zeit-Geschwindigkeit-Gesetz
Für die Geschwindigkeiten der Bahnkurve des Körpers beim schiefen Wurf finden wir ein zum „Zeit-Ort-Gesetz“ analoges „Zeit-Geschwindigkeit-Gesetz“
 .
.
Auch hier sehen wir die Gleichförmigkeit der  -Bewegung und die Beschleunigung in
-Bewegung und die Beschleunigung in  -Richtung. In
-Richtung. In  -Richtung bleibt die Geschwindigkeit bei der konstante Anfangsgeschwindigkeit
-Richtung bleibt die Geschwindigkeit bei der konstante Anfangsgeschwindigkeit  , während sie in in
, während sie in in  -Richtung immer weiter abnimmt.
-Richtung immer weiter abnimmt.
Schräger Wurf Flugbahn berechnen
Betrachten wir nun die Flugbahn eines solchen schiefen Wurfes und bestimmen einige charakteristische Größen, im Speziellen die Wurfhöhe und –weite sowie die Steig– und Fallzeit und die insgesamte Flugzeit, bis der Körper (wieder) auf den Boden bei  trifft. Dafür setzen wir fürs Erste die Anfangshöhe des Körpers auf Null,
trifft. Dafür setzen wir fürs Erste die Anfangshöhe des Körpers auf Null,  , und werfen also vom Boden aus. Wir können außerdem immer
, und werfen also vom Boden aus. Wir können außerdem immer  wählen, da wir es in dieser Richtung nur mit einer gleichförmigen Bewegung zu tun haben.
wählen, da wir es in dieser Richtung nur mit einer gleichförmigen Bewegung zu tun haben.
Wurfhöhe und Steigzeit
Uns interessiert zuerst, wie hoch der Körper beim schiefen Wurf maximal geworfen wird und wie lange er bis zu dieser Wurfhöhe braucht. Die maximale Höhe ist durch  charakterisiert. Der Körper erreicht also den Scheitelpunkt seiner Bewegung, bleibt bei der maximalen Höhe kurz stehen und fällt dann zu Boden. Dadurch bestimmen wir die Steigzeit
charakterisiert. Der Körper erreicht also den Scheitelpunkt seiner Bewegung, bleibt bei der maximalen Höhe kurz stehen und fällt dann zu Boden. Dadurch bestimmen wir die Steigzeit  wie folgt
wie folgt
 .
.
Mit der Steigzeit können wir jetzt die maximale Wurfhöhe  berechnen
berechnen
 .
.
Wir sehen, dass die Steigzeit und die Wurfhöhe für  maximal werden. Das entspricht dem Wurf gerade nach oben.
maximal werden. Das entspricht dem Wurf gerade nach oben.
Wurfweite und Flugzeit
Die maximale Weite des schrägen Wurfes wird dadurch bestimmt, wann der Körper (wieder) den Boden erreicht, also wann  gilt. Aus dieser Bedingung können wir die Flugzeit
gilt. Aus dieser Bedingung können wir die Flugzeit  berechnen
berechnen
 .
.
Diese Gleichung hat zwei Lösungen:  , was dem Start am Boden entspricht und
, was dem Start am Boden entspricht und
 ,
,
was die Zeit bis zum „Ende des schiefen Wurfes“ angibt. Jetzt können wir mit  die Wurfweite
die Wurfweite  berechnen
berechnen
 ,
,
wobei wir  verwendet haben. Hier sehen wir jetzt, dass wir für
verwendet haben. Hier sehen wir jetzt, dass wir für  eine Wurfweite von
eine Wurfweite von  erhalten – wenn wir gerade nach oben werfen, kommen wir natürlich nicht besonders weit – und sich für
erhalten – wenn wir gerade nach oben werfen, kommen wir natürlich nicht besonders weit – und sich für  die maximale Weite
die maximale Weite  ergibt. Letzteres entspricht dem Wurf im 45 Grad-Winkel.
ergibt. Letzteres entspricht dem Wurf im 45 Grad-Winkel.
Fallzeit
Zuletzt bestimmen wir noch die Fallzeit  , also die Zeit, die der Körper vom höchsten Punkt bis zum auftreffen auf dem Boden benötigt. Wir finden sie gegeben als
, also die Zeit, die der Körper vom höchsten Punkt bis zum auftreffen auf dem Boden benötigt. Wir finden sie gegeben als
 .
.
Die Steig- und Fallzeit sind gleich und die Bewegung also symmetrisch, sodass die Endgeschwindigkeit des Körpers am Boden  beträgt.
beträgt.
Schiefer Wurf Wurfparabel
Wie aber sehen wir, dass die Flugbahn beim schiefen Wurf eine Parabel ist? Dazu müssen wir die Flugbahn reparametrisieren und  anstelle von
anstelle von  als Parameter verwenden. So können wir die Bahnkurve berechnen, indem wir
als Parameter verwenden. So können wir die Bahnkurve berechnen, indem wir  als Funktion von
als Funktion von  angeben. Hierfür invertieren wir zuerst
angeben. Hierfür invertieren wir zuerst 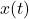
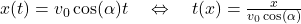 .
.
Jetzt setzen wir  in die Funktion
in die Funktion  ein und erhalten insgesamt eine Abhängigkeit
ein und erhalten insgesamt eine Abhängigkeit 
 .
.
Wir haben die Bahngleichung der Wurfparabel bestimmt.
Schräger Wurf mit Anfangshöhe
Zu Beginn unserer Rechnungen zum schiefen Wurf haben wir  gesetzt. Das ist natürlich nicht der allgemeine Fall. Im Allgemeinen werfen wir nicht vom Boden aus, sondern von einer Anfangshöhe
gesetzt. Das ist natürlich nicht der allgemeine Fall. Im Allgemeinen werfen wir nicht vom Boden aus, sondern von einer Anfangshöhe  . Wir können aber immer noch
. Wir können aber immer noch  behalten.
behalten.
Die Steigzeit  bleibt von der neuen Anfangshöhe natürlich unbeeinflusst und wir finden analog zu vorher die neue Wurfhöhe
bleibt von der neuen Anfangshöhe natürlich unbeeinflusst und wir finden analog zu vorher die neue Wurfhöhe
 .
.
Für die Flug- und Fallzeit  und
und  sowie die insgesamte Wurfweite
sowie die insgesamte Wurfweite  des schiefen Wurfes finden wir jetzt aber natürlich andere Formeln. Die Flugdauer bestimmen wir wieder über den Auftreffpunkt des Körpers am Boden
des schiefen Wurfes finden wir jetzt aber natürlich andere Formeln. Die Flugdauer bestimmen wir wieder über den Auftreffpunkt des Körpers am Boden  und erhalten
und erhalten
 .
.
Das dem Minus entsprechende  entspricht der in der Vergangenheit liegenden Zeit, zu der das System am Boden hätte starten müssen, um ein schiefer Wurf vom Boden wie oben zu sein. Dem Plus entspricht
entspricht der in der Vergangenheit liegenden Zeit, zu der das System am Boden hätte starten müssen, um ein schiefer Wurf vom Boden wie oben zu sein. Dem Plus entspricht  , die Flugzeit bis zum Ende des schiefen Wurfes, die wir zur Bestimmung der Wurfweite verwenden
, die Flugzeit bis zum Ende des schiefen Wurfes, die wir zur Bestimmung der Wurfweite verwenden
 ,
,
wobei wir für den ersten Summanden wieder  genutzt haben. Hier ist wichtig, zu beachten dass die maximale Wurfweite jetzt nicht mehr für
genutzt haben. Hier ist wichtig, zu beachten dass die maximale Wurfweite jetzt nicht mehr für  erreicht wird, stattdessen ist der „perfekte Winkel“
erreicht wird, stattdessen ist der „perfekte Winkel“  jetzt wie folgt gegeben
jetzt wie folgt gegeben
 ,
,
was für  in
in  , also
, also  , übergeht.
, übergeht.
Für die Fallzeit ergibt sich jetzt
 .
.
Schiefer Wurf Aufgaben
Zuletzt wollen wir noch ein paar kurze Aufgaben zum schrägen Wurf durchrechnen. Wir wollen einen Ball mit 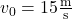 unter einem Winkel von
unter einem Winkel von  vom Boden abwerfen. Wie hoch und weit kommt er also? Setzen wir einmal ein
vom Boden abwerfen. Wie hoch und weit kommt er also? Setzen wir einmal ein
 .
.
Und jetzt lassen wir den schiefen Wurf nicht am Boden beginnen, sondern starten bei einer Anfangshöhe von  . Wie weit kommen wir jetzt? Auch hier hilft simples Einsetzen
. Wie weit kommen wir jetzt? Auch hier hilft simples Einsetzen

und wir sehen, dass wir mehr als doppelt so weit kommen.

