Druck
Ob Arzt, Taucher oder Physiker, jeder kommt mit Druck in Kontakt. Was der Druck genau ist und wie die wichtigsten Formeln und Einheiten aussehen, lernst du in unserem Beitrag. Hier geht es direkt zum Video !
Inhaltsübersicht
Druck einfach erklärt
Der Druck p in der Physik beschreibt, welche Kraft auf eine Fläche von einem Quadratmeter wirkt. Du findest dafür oft die Sprechweise: „Druck p ist gleich Kraft pro Fläche.“
Daher kannst du den Druck p auch als Quotient aus Kraft F geteilt durch Fläche A ausrechnen:
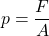
Die Einheit des Drucks ist Newton pro Quadratmeter oder das Pascal (Pa):
![Rendered by QuickLaTeX.com [p] = \dfrac{\text{N}}{\text{m}^2} = \text{Pa}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-80fe5e5e78a12cfd00d66be90798177e_l3.png)
Erhöhst du die Kraft F bei gleicher Fläche A, dann erhöht sich auch der Druck p. Vergrößerst du hingegen die Fläche A, ohne die Kraft F zu verändern, verringert sich der Druck.
Der Druck p gibt das Verhältnis von Kraft F pro Fläche A an. Er ist insbesondere in zwei Situationen von großer Bedeutung: Als Druck innerhalb von Flüssigkeiten und Gasen; und als Druck, der von einem Festkörper auf einen anderen Körper ausgeübt wird.
Was ist Druck?
Wenn du eine Kraft  und Fläche
und Fläche  gegeben hast, dann kannst du den Druck p mit der Definition
gegeben hast, dann kannst du den Druck p mit der Definition
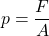
berechnen. Hier ist es wichtig, dass nur der senkrechte Anteil der Kraft
 verwendet wird. Um das hervorzuheben, findest du dafür in der Physik auch die Bezeichnung
verwendet wird. Um das hervorzuheben, findest du dafür in der Physik auch die Bezeichnung  . Das Zeichen
. Das Zeichen  soll an einen rechten Winkel erinnern. Mit dieser Bezeichnung sieht dann die Formel für den Druck p so aus:
soll an einen rechten Winkel erinnern. Mit dieser Bezeichnung sieht dann die Formel für den Druck p so aus:

Vielleicht hast du dich schon einmal gefragt, wieso du mit einem Messer relativ leicht Brot (oder andere Lebensmittel) schneiden kannst, ohne viel Kraft aufwenden zu müssen. Das liegt daran, dass die Messerklinge hauchdünn ist. Du hast also eine sehr kleine Fläche. Damit kannst du bereits bei einer kleinen Kraft einen sehr hohen Druck ausüben.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Druck Abhängigkeit von Kraft und Fläche
Das Beispiel mit dem Messer hilft uns auch zu verstehen, wie genau der Druck von Kraft und Fläche abhängt:
(1) Vergrößerst du die Kraft (drückst du also stärker mit dem Messer), lässt aber die Fläche gleich, so erhöht sich der Druck.
(2) Machst du hingegen die Fläche kleiner (schärfst du z.B. das Messer), lässt aber die Kraft gleich, so wird der Druck ebenfalls größer.
Der Druck berücksichtigt beides: welche Kraft  ausgeübt wird und wie groß die Fläche
ausgeübt wird und wie groß die Fläche  ist, auf die die Kraft
ist, auf die die Kraft  wirkt. Die einfach zu merkende Sprechweise „Kraft pro Fläche“ fasst genau das zusammen.
wirkt. Die einfach zu merkende Sprechweise „Kraft pro Fläche“ fasst genau das zusammen.
Druck Einheit
Als Quotient aus Kraft und Fläche besitzt der Druck die Einheit Newton ( ) pro Quadratmeter (
) pro Quadratmeter ( ):
):
![Rendered by QuickLaTeX.com [p] = \dfrac{\text{N}}{\text{m}^2}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-30cb44f6bdd512f21207dcaafde570fa_l3.png)
Dafür wurde auch die kürzere Bezeichnung Pascal ( ) eingeführt, das heißt:
) eingeführt, das heißt:
![Rendered by QuickLaTeX.com [p] = \dfrac{\text{N}}{\text{m}^2} = \text{Pa}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-80fe5e5e78a12cfd00d66be90798177e_l3.png)
Neben dem Pascal findest du auch das Bar als weitere Einheit für den Druck. Zwischen der Einheit Pascal und der Einheit Bar gibt es folgende Beziehung:

Der Atmosphärische Druck beträgt etwa 1 bar. In Pascal würde er also  betragen.
betragen.
Druck Physik Beispiele
In der Tabelle erkennst du, dass zum Beispiel ein 5€-Schein, der flach auf einem Tisch ruht, einen Druck von etwa  ausübt. Wir Menschen können mit unserem Biss einen Druck von bis zu
ausübt. Wir Menschen können mit unserem Biss einen Druck von bis zu  hervorrufen.
hervorrufen.
| Beispiel | Druck |
| Druck eines 5€-Scheins, der flach auf dem Tisch liegt |  |
| Druck, der von einem leichten Windzug ausgeübt wird |  |
| Druck, der von der Lunge einer gesunden Person ausgeübt werden kann |  |
| Blutdruck bei einem gesunden Erwachsenen |  |
| Druck eines durchschnittlichen menschlichen Bisses |  |
Druck in Flüssigkeiten und Gasen
Je nach Art von Medium kannst du den Druck unterschiedlich betrachten. Wir schauen uns zwei konkrete Beispiele an: ruhende Flüssigkeiten und ideale Gase.
Beginnen wir mit ruhenden Flüssigkeiten. Du kannst dir ein Glas mit Wasser vorstellen.
In dieser Situation findest du den Begriff des Hydrostatischen Drucks . Er ist insbesondere durch zwei Eigenschaften charakterisiert:
(1) Er besitzt innerhalb einer Flüssigkeit in allen Richtungen denselben Betrag.
(2) Er wirkt immer senkrecht auf jede Fläche, die im Kontakt mit der Flüssigkeit steht.
Ein wichtiges Prinzip im Zusammenhang mit dem hydrostatischen Druck ist das Pascal’sche Prinzip : Das Pascal’sche Prinzip sagt aus, dass der Druck, der auf eine eingeschlossene Flüssigkeit ausgeübt wird, sich unverändert auf jedes Flüssigkeitsteilchen verteilt.
Eine sehr anschauliche Anwendung, die sich das Prinzip zu Nutze macht, ist die hydraulische Hebebühne. Dabei erzeugt eine Kraft  , die auf die Fläche
, die auf die Fläche  des kleinen Kolbens wirkt, eine Änderung im Druck, die auf die Fläche
des kleinen Kolbens wirkt, eine Änderung im Druck, die auf die Fläche  des großen Kolbens übertragen wird. Es resultiert damit eine viel größere Kraft
des großen Kolbens übertragen wird. Es resultiert damit eine viel größere Kraft  auf den großen Kolben. Dadurch kann eine kleine Kraft zu einer großen Kraft verstärkt werden.
auf den großen Kolben. Dadurch kann eine kleine Kraft zu einer großen Kraft verstärkt werden.
Für Gase gelten ebenso die Aussagen (1) und (2), die für ruhende Flüssigkeiten gelten. Ein sehr wichtiges Beispiel für Gase sind die sogenannten idealen Gase . Dabei handelt es sich um eine Vereinfachung in der Physik von Gasen, bei der die Größe der Gasteilchen sowie deren Anziehungskräfte untereinander ignoriert werden und nur elastische Stöße von Interesse sind.
Hier lässt sich der Druck p folgendermaßen berechnen:

Wobei  die Stoffmenge
,
die Stoffmenge
, 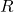 die Gaskonstante,
die Gaskonstante,  bzw.
bzw.  die Temperatur bzw. das Volumen des Gases sind.
die Temperatur bzw. das Volumen des Gases sind.
Druck berechnen
Um den Druck zu berechnen, betrachten wir das Beispiel einer einfachen Hebebühne. Du hast einen großen Kolben mit einer Fläche  und einen kleinen Kolben mit einer Fläche
und einen kleinen Kolben mit einer Fläche  . Welchen Druck musst du dann auf den kleinen Kolben ausüben, damit der große Kolben einen Wagen der Masse
. Welchen Druck musst du dann auf den kleinen Kolben ausüben, damit der große Kolben einen Wagen der Masse  heben kann?
heben kann?
Wir wissen, dass die Gleichung

gilt und interessieren uns hier für den Druck  auf den kleinen Kolben.
auf den kleinen Kolben.
Die Kraft  , die auf den großen Kolben wirkt, entspricht gerade der Gewichtskraft
des Wagens. Wir erhalten also für
, die auf den großen Kolben wirkt, entspricht gerade der Gewichtskraft
des Wagens. Wir erhalten also für  :
:

Du musst also einen Druck von  aufwenden.
aufwenden.
Luftdruck und Schall
Der Druck spielt auch im Alltag eine sehr wichtige Rolle. Die Änderung im Luftdruck ist zum Beispiel dafür verantwortlich, dass wir Geräusche hören können. Wie und warum genau der Druck und der Schall zusammenhängen, erklären wir dir ausführlich in unserem Beitrag zum Schall.



