Video

Quiz

Kreisbewegung

Wichtige Inhalte in diesem Video

Kreisbewegung einfach erklärt

Was ist eine Kreisbewegung?

Kreisbewegung Größen

Umlaufdauer und Frequenz

Bahngeschwindigkeit und Winkelgeschwindigkeit

Kreisbewegung Berechnen

Sitzt du in einem Karussell, drehst du dich ständig im Kreis, fühlst aber wie dein Körper nach außen gedrückt wird. Was es damit auf sich hat und was Kreisbewegungen für eine besondere Bedeutung in der Natur haben, das erfährst du hier.

Schau auf jeden Fall noch das Video zum Artikel an. Darin sind die wichtigsten Punkte für dich noch mal in Wort und Bild aufbereitet.

Inhaltsübersicht

Kreisbewegung einfach erklärt

im Videozur Stelle im Video springen

Unter einer Kreisbewegung kannst du eine Bewegung, deren Bahn auf einem Kreis verläuft, vorstellen. Der Betrag ihrer Geschwindigkeit sowie ihr Radius sind konstant. Wegen der konstanten Geschwindigkeit, handelt es sich um eine gleichförmige Kreisbewegung. Damit ein Körper auf einer Kreisbahn bleibt, muss dieser ständig in Richtung des Mittelpunktes beschleunigt werden. Durch diese Beschleunigung ändert sich also immer die Richtung der Bewegung, sodass der Körper auf der Kreisbahn bleibt. Eine Kreisbewegung ist also auch eine beschleunigte Bewegung.

Was ist eine Kreisbewegung?

im Videozur Stelle im Video springen

Im Gegensatz zur gleichförmigen Bewegung, also der geradlinigen Bewegung mit konstanter Geschwindigkeit, ändert sich die Bewegungsrichtung und somit die Richtung der Geschwindigkeit auf einer Kreisbahn ständig.

Ein Körper, welcher sich auf einer Kreisbahn bewegt, hat eine Geschwindigkeit. Diese bezeichnest du als Bahngeschwindigkeit. Hat diese Geschwindigkeit einen konstanten Betrag, so handelt es sich um eine gleichförmige Kreisbewegung.

Gleichförmige Kreisbewegung

Bei einer gleichförmigen Kreisbewegung bewegt sich ein Körper auf einer Kreisbahn, auf welcher er in gleich langen Zeitintervallen gleich lange Wege zurücklegt.
Bei dieser Bewegung ist der Betrag der Geschwindigkeit konstant, nicht aber die Richtung der Bewegung.

Kreis, Kreisbewegung, konstante Geschwindigkeit, Radius, Bewegung, gleichförmige Bewegung — Ein Körper bewegt sich mit konstanter Geschwindigkeit v im Abstand r um den Mittelpunkt. Egal wo auf dem Kreis sich der Körper befindet, die Geschwindigkeit v bleibt immer gleich groß.

Auf der Abbildung siehst du das deutlich. Der rote Ball bewegt sich auf einer Kreisbahn um den Mittelpunkt. Misst du die Geschwindigkeit des Balles an einem Punkt auf der Kreisbahn und später an einem ganz anderen Punkt, siehst du, dass diese immer gleich bleibt. Die Bahngeschwindigkeit ist also konstant.

Kreisbewegung Größen

im Videozur Stelle im Video springen

Hier siehst du wichtigsten Größen zur Beschreibung einer Kreisbewegung.

Bahngeschwindigkeit : Das ist die Geschwindigkeit, des Körpers auf der Kreisbahn. Bei einer gleichförmigen Kreisbewegung ist sie konstant. Ihre Einheit ist Meter pro Sekunde (m/s).

Umlaufdauer : Das ist die Zeit, welche der Körper für einen Umlauf der Kreisbahn benötigt. Sie hat die Einheit der Sekunde (s)

Radius : Das ist die Entfernung des Körpers zum Mittelpunkt des Kreises. Den Radius gibst du in Metern an (m).

Frequenz : Die Frequenz sagt dir wie viele Umläufe der Körper auf der Kreisbahn pro Sekunde macht. Die Einheit der Frequenz ist Hertz (Hz oder 1/s).

Umlaufdauer und Frequenz

im Videozur Stelle im Video springen

Die Umlaufdauer steht in Zusammenhang mit der Frequenz, welche dir angibt, wie viele Umläufe der Körper pro Zeiteinheit macht: $f=\frac{N}{t}$

Die Formel für die Frequenz ist: $f=\frac{1}{T}$

Die Formel für die Umlaufdauer ist: $T=\frac{1}{f}$

Bahngeschwindigkeit und Winkelgeschwindigkeit

im Videozur Stelle im Video springen

Für den Betrag der Bahngeschwindigkeit gilt: $v=\frac{\Delta s}{\Delta t}=konst.$
Hier stehen $\Delta s$ und $\Delta t$ für ein kleines Strecken- beziehungsweise Zeitintervall. Die Formel sagt dir also, dass die Länge der Strecke nach verstreichen eines gewissen Zeitraums, immer gleich bleibt.

Du weißt nun, dass der Körper bei seiner Kreisbewegung in der Zeit ein Mal den Kreis umläuft. Diese Strecke entspricht also dem Umfang des Kreises in Abhängigkeit des Radius: $U=2\pi r$

Hierüber drückst du jetzt die Bahngeschwindigkeit aus:

$v=\frac{\Delta s}{\Delta t}= \frac{2\pi r}{T}$

Mit dem zuvor gezeigten Zusammenhang zwischen Frequenz und Umlaufzeit sieht diese Formel dann wie folgt aus:

$v= 2\pi rf$

Wie du hier siehst, ist die Bahngeschwindigkeit abhängig vom Radius. Das ist aber nicht immer wünschenswert. Alternativ betrachtest du dir hierzu die Winkelgeschwindigkeit $\omega$ . Sie sagt dir, was für ein Winkel $\phi$ in einem bestimmten Zeitintervall $\Delta t$ überstrichen wurde.

$\omega = \frac{\Delta \phi}{\Delta t}$

Du misst den Winkel nicht in Grad, sondern im Bogenmaß . Ein Umlauf auf dem Kreis entspricht 360°. Im Bogenmaß wird in einer Umlaufdauer ein Winkel von $\phi = 2 \pi$ überstrichen.

Damit erhältst du für die Winkelgeschwindigkeit:

$\omega = \frac{2 \pi}{T} = 2 \pi f$

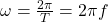
Betrachtest du das im Zusammenhang mit der Bahngeschwindigkeit $v=2 \pi rf$ ergibt sich für die Bahngeschwindigkeit der folgende Ausdruck:

$v=\omega r$

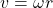
Kreisbewegung Formeln

Nachdem du jetzt weißt, was eine Kreisbewegung ist, findest du hier alle wichtigen Formeln nochmal zusammengefasst. Kennst du diese, sind Kreisbewegungen für dich kein Problem mehr.

Größe	Symbol	Einheit	Bedeutung	Formel
Periode	T	s	Umlaufdauer	$T=\frac{1}{f}$
Frequenz	f	Hz	Umläufe pro Sekunde	$f=\frac{1}{T}$
Radius	r	m	Abstand zum Mittelpunkt
Bahngeschwindigkeit	v	m/s	Geschwindigkeit des Körpers	$v = \frac{2 \pi r}{T}$ $v=2 \pi r f$ $v=\omega r$
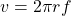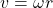
Bahnbeschleunigung	a	m/s	Beschleunigung zum MIttelpunkt	$a=\frac{v^2}{r}$
Winkelgeschwindigkeit	$\omega$	1/s	Überstrichener Winkel pro Sekunde	$\omega = \frac{\Delta \phi}{\Delta t}$ $\omega = \frac{2 \pi}{T}$ $\omega = 2\pi f$

Kreisbewegung Berechnen

im Videozur Stelle im Video springen

Abschließend nutzen wir unser neu gewonnenes Wissen und berechnen damit, wie schnell sich der Mond um die Erde bewegt.

Dazu brauchst du zwei Werte: den Bahnradius , also den Abstand des Mondes zur Erde und die Umlaufdauer , also wie lange der Mond braucht um die Erde zu umrunden.

Der Mond ist im Mittel von der Erde 384.000 km entfernt. Also erhalten wir r=384.000 km.

Eine Umrundung des Mondes dauert 27,3 Tage. Damit erhalten wir also $T=27,3 \, Tage = 655,2 \, h$

Diese Werte setzt du nun einfach in deine Formel für die Bahngeschwindigkeit ein:

$v= \frac{2\pi r}{T} = \frac{2\pi \cdot 384.000 \, km}{655,2 \, h} = 3.682 \, \frac{km}{h}$ .

damit weißt du jetzt, dass sich der Mond mit ungefähr 3.680 km/h um die Erde bewegt. Ganz schön schnell!

Mond, Erde, Kreisbewegung, Bahngeschwindigkeit, gleichförmige Kreisbewegung — Der Mond bewegt sich um die Erde

Kreisbewegung und Zentripetalkraft

im Videozum Video springen

Wie du am Anfang erfahren hast, muss der Körper zum Mittelpunkt des Kreises beschleunigt werden, damit die Bewegung auf der Kreisbahn erhalten bleibt. Das heißt, dass eine ständige Kraft auf diesen Körper wirkt. Diese Kraft bezeichnest du als Zentripetalkraft und entsprechend die Beschleunigung des Körpers zur Mitte als Zentripetalbeschleunigung.

Schau dazu am besten noch unser für dich vorbereitetes Video an. Darin erfährst du alles wichtige zu dieser Kraft.

Zum Video: Zentripetalkraft und Zentrifugalkraft

zur Videoseite: Kreisbewegung

Beliebte Inhalte aus dem Bereich Mechanik

Zentripetalkraft und Zentrifugalkraft

Zentrifugalkraft

Trägheitsgesetz

Massenträgheitsmoment

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .