Warum reicht beim Globalverhalten wirklich nur der höchste Exponent?

Beim Globalverhalten reicht der höchste Exponent, weil dieser Term für große Beträge von am schnellsten wächst. Alle Terme mit kleineren Exponenten werden im Vergleich dazu immer unbedeutender, egal welche Vorfaktoren sie haben. Beispiel: Für große dominiert gegenüber und .

Wie bestimme ich das Globalverhalten, wenn der höchste Term fehlt?

Wenn der höchste Term „fehlt“, ist sein Vorfaktor und du nimmst den nächsthöheren Term mit . Das ist dann der neue führende Term und bestimmt Grad und Vorzeichen für das Globalverhalten. Beispiel: Aus wird führend.

Welche Fehler passieren oft beim Ablesen von Vorzeichen und Grad?

Häufige Fehler sind, das Minuszeichen vor dem führenden Term zu übersehen und den Grad falsch zu erkennen. Typisch ist auch, einen kleineren Exponenten zu nehmen, weil er „auffälliger“ aussieht. Beispiel: Bei ist der Grad und der führende Vorfaktor ist positiv, nicht negativ.

Wie erkenne ich das Globalverhalten bei Funktionen mit Klammern?

Bei Funktionen mit Klammern erkennst du das Globalverhalten, indem du den führenden Term nach dem Ausmultiplizieren oder durch Abschätzen bestimmst. Entscheidend ist wieder der höchste Exponent und sein Vorfaktor. Beispiel: hat führend , also gerader Grad und positiver Vorfaktor.

Wie unterscheide ich Globalverhalten und Verhalten an einer Stelle?

Globalverhalten beschreibt, was mit passiert, wenn oder . Das Verhalten an einer Stelle betrachtet dagegen, was nahe einem bestimmten -Wert passiert, zum Beispiel bei oder an einer Nullstelle. Beispiel: wächst global nach rechts, hat aber lokal bei den Wert .

Video

Quiz

Hier geht's zum Video „Ganzrationale Funktionen“

Globalverhalten

Was ist das Globalverhalten und wie bestimmst du es? Das zeigen wir dir jetzt in unserem Beitrag und in unserem Video !

Inhaltsübersicht

Globalverhalten einfach erklärt

im Videozur Stelle im Video springen

(00:14)

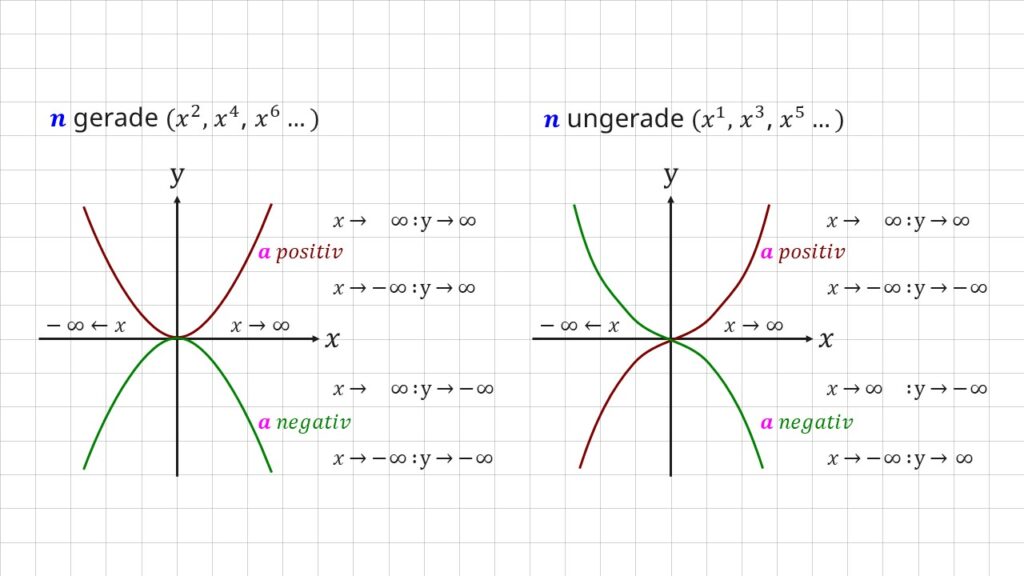
Beim Globalverhalten beobachtest du, wie sich deine y-Werte verhalten, wenn du sehr große x-Werte in die Funktion einsetzt. Dafür schaust du dir zunächst den Vorfaktor und den Grad der Funktion an:

f(x)= -5x⁴+ 3x³+ 5

Wichtig: Du betrachtest nur das x mit dem größten Exponenten n. Denn der Globalverlauf einer Funktion wird ausschließlich von dem größten x-Exponenten in Kombination mit dem Vorfaktor a bestimmt!

Du unterscheidest beim Globalverlauf nur, ob der Vorfaktor positiv oder negativ ist und ob der Grad der Funktion gerade oder ungerade ist.

globalverhalten, globalverhalten bestimmen, globalverhalten ganzrationaler funktionen, global verhalten, globalverhalten Mathe, globalverlauf, globalverlauf ganzrationaler funktionen, globalverhalten einer funktion — Globalverhalten von Funktionen

Das schauen wir uns an einem Beispiel mal genauer an.

Globalverhalten — Beispiel

Betrachte die Funktion f(x) = -2x⁸+ x⁵+3x +2

Bestimme nun Vorfaktor und Grad der Funktion vom größten Exponenten.
→ -2x⁸ → a ist negativ und n ist gerade
Schau in der Übersicht zu welchem Graphen die Kombination passt.
x → ∞ : y → −∞ und x → −∞ : y → −∞ ist dein Globalverhalten.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Globalverhalten — häufigste Fragen

(ausklappen)

Warum reicht beim Globalverhalten wirklich nur der höchste Exponent?

Beim Globalverhalten reicht der höchste Exponent, weil dieser Term für große Beträge von am schnellsten wächst. Alle Terme mit kleineren Exponenten werden im Vergleich dazu immer unbedeutender, egal welche Vorfaktoren sie haben. Beispiel: Für große dominiert gegenüber und .
Wie bestimme ich das Globalverhalten, wenn der höchste Term fehlt?

Wenn der höchste Term „fehlt“, ist sein Vorfaktor und du nimmst den nächsthöheren Term mit $a \neq 0$ . Das ist dann der neue führende Term und bestimmt Grad und Vorzeichen für das Globalverhalten. Beispiel: Aus $0\cdot x^5-2x^3+x$ wird führend.
Welche Fehler passieren oft beim Ablesen von Vorzeichen und Grad?

Häufige Fehler sind, das Minuszeichen vor dem führenden Term zu übersehen und den Grad falsch zu erkennen. Typisch ist auch, einen kleineren Exponenten zu nehmen, weil er „auffälliger“ aussieht. Beispiel: Bei ist der Grad und der führende Vorfaktor ist positiv, nicht negativ.
Wie erkenne ich das Globalverhalten bei Funktionen mit Klammern?

Bei Funktionen mit Klammern erkennst du das Globalverhalten, indem du den führenden Term nach dem Ausmultiplizieren oder durch Abschätzen bestimmst. Entscheidend ist wieder der höchste Exponent und sein Vorfaktor. Beispiel: hat führend , also gerader Grad und positiver Vorfaktor.
Wie unterscheide ich Globalverhalten und Verhalten an einer Stelle?

Globalverhalten beschreibt, was mit passiert, wenn $x \to \infty$ oder $x \to -\infty$ . Das Verhalten an einer Stelle betrachtet dagegen, was nahe einem bestimmten -Wert passiert, zum Beispiel bei oder an einer Nullstelle. Beispiel: wächst global nach rechts, hat aber lokal bei den Wert .

Ganzrationale Funktionen

Jetzt kennst du dich mit dem Globalverhalten von ganzrationalen Funktionen aus. Ganzrationale Funktionen haben aber auch noch weitere Eigenschaften! Welche das sind, erfährst du in unserem Video dazu!