Totale Differenzierbarkeit
Im Fall der totalen Differenzierbarkeit werden Abbildungen einer offenen Teilmenge des  in den
in den  betrachtet. Wie man die totale Differenzierbarkeit besser aufzeigen kann, erklären wir dir am Ende mit zwei Beispielen.
betrachtet. Wie man die totale Differenzierbarkeit besser aufzeigen kann, erklären wir dir am Ende mit zwei Beispielen.
Totale Differenzierbarkeit – total schwierig? Überhaupt nicht! in unserem Video verstehst du das Thema in unter 4 Minuten!
Inhaltsübersicht
Motivation und Vorüberlegungen zur totalen Differenzierbarkeit
Eine reellwertige Funktion einer Variablen  ist an der Stelle
ist an der Stelle  bekanntlich genau dann differenzierbar, falls der Grenzwert
bekanntlich genau dann differenzierbar, falls der Grenzwert
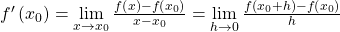
existiert. Der Grenzwert wird als Differentialquotient
bzw. Ableitung von  an der Stelle
an der Stelle  bezeichnet. Dieser Differenzierbarkeitsbegriff lässt sich allerdings nicht gut auf mehrdimensionale Funktionen
bezeichnet. Dieser Differenzierbarkeitsbegriff lässt sich allerdings nicht gut auf mehrdimensionale Funktionen  übertragen. Daher wird hierfür eine andere mögliche Definition der Differenzierbarkeit für reellwertige Funktionen einer Variablen betrachtet.
übertragen. Daher wird hierfür eine andere mögliche Definition der Differenzierbarkeit für reellwertige Funktionen einer Variablen betrachtet.
 in
in  differenzierbar, so lässt sich die Funktion durch eine affin lineare Funktion g nähern. Man spricht dabei von Linearisierung
bzw. Linearer Approximation.
differenzierbar, so lässt sich die Funktion durch eine affin lineare Funktion g nähern. Man spricht dabei von Linearisierung
bzw. Linearer Approximation.Die affin lineare Näherungsfunktion g beschreibt dabei die Tangente an den Funktionsgraphen von  an der Stelle
an der Stelle  . Diese Tangente besitzt bekanntlich gerade die Steigung
. Diese Tangente besitzt bekanntlich gerade die Steigung  . Die Näherungsfunktion g lauter demnach:
. Die Näherungsfunktion g lauter demnach:

Für die Restfunktion  , welche die Differenz zwischen
, welche die Differenz zwischen  und
und  beschreibt, gilt dann:
beschreibt, gilt dann:


Die Idee der linearen Approximierbarkeit differenzierbarer Funktionen wird nun auf mehrdimensionale Funktionen übertragen.
Definition: Totale Differenzierbarkeit
Sei  offen und
offen und  eine Funktion.
eine Funktion.  heißt an der Stelle
heißt an der Stelle  total differenzierbar, falls eine lineare Abbildung
total differenzierbar, falls eine lineare Abbildung  existiert, sodass in einer Umgebung von
existiert, sodass in einer Umgebung von  gilt:
gilt:
Dabei muss die Funktion  in einer Umgebung von
in einer Umgebung von  definiert sein.
definiert sein.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Totale Ableitung
Die lineare Abbildung  kann durch eine
kann durch eine  – Matrix beschrieben werden, welche als totale Ableitung, totales Differential, Funktionalmatrix oder Jacobi-Matrix
bezeichnet wird:
– Matrix beschrieben werden, welche als totale Ableitung, totales Differential, Funktionalmatrix oder Jacobi-Matrix
bezeichnet wird:


Wird  durch
durch  ersetzt, so wird der Grenzübergang
ersetzt, so wird der Grenzübergang  zu
zu  und eine äquivalente Formulierung der beiden obigen Bedingungen lautet:
und eine äquivalente Formulierung der beiden obigen Bedingungen lautet:
Eine Funktion  ist im Allgemeinen also dann in
ist im Allgemeinen also dann in  total differenzierbar, wenn sie sich gut durch eine affin lineare Funktion
total differenzierbar, wenn sie sich gut durch eine affin lineare Funktion  approximieren lässt.
approximieren lässt.

-

 Konstante („Ableitung“)
Konstante („Ableitung“) -

 Lineare Abbildung
Lineare Abbildung -

 Lineare Approximation
Lineare Approximation -

 Restfunktion
Restfunktion  ist differenzierbar in
ist differenzierbar in  , wenn gilt:
, wenn gilt:


-


 -Matrix (Totale Ableitung)
-Matrix (Totale Ableitung) -

 Lineare Abbildung
Lineare Abbildung -
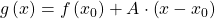
 Lineare Approximation
Lineare Approximation -

 Restfunktion
Restfunktion  ist total differenzierbar in
ist total differenzierbar in  , wenn gilt:
, wenn gilt:

Jacobi-Matrix berechnen
Sei die Funktion  in
in  total differenzierbar und es gelte
total differenzierbar und es gelte  mit der Matrix
mit der Matrix  und dem Vektor
und dem Vektor  , dann sind alle Komponenten
, dann sind alle Komponenten  (mit
(mit  ) der Funktion
) der Funktion  in
in  partiell differenzierbar
und es gilt:
partiell differenzierbar
und es gilt:
 .
.
Um dies zu zeigen, wird zunächst die  -te Komponente von
-te Komponente von  betrachtet:
betrachtet:

Damit gilt mit dem  -ten Einheitsvektor
-ten Einheitsvektor  und der
und der  -ten Komponente
-ten Komponente  des Vektors
des Vektors  :
:

Und es gilt:

Die Einträge der Jacobi-Matrix sind also die partiellen Ableitungen der einzelnen Komponenten von  .
.
Totale Differenzierbarkeit reellwertiger Funktionen
Für reellwertige Funktionen lässt sich außerdemn folgendes zeigen: Sei  auf der offenen Menge
auf der offenen Menge  partiell differenzierbar und alle partiellen Ableitungen seien
partiell differenzierbar und alle partiellen Ableitungen seien  stetig. Dann ist
stetig. Dann ist  in
in  total differenzierbar.
total differenzierbar.
Schaubild der Implikationen
Zusammenfassend gelten die folgenden Implikationen:
Stetig partiell differenzierbar (für reellwertige Funktionen)

Total differenzierbar  stetig
stetig

Partiell differenzierbar
Die Umkehrungen dieser Aussagen gelten im Allgemeinen allerdings nicht.
Totale Differenzierbarkeit zeigen Beispiele
Um die totale Differenzierbarkeit einer Funktion  an der Stelle
an der Stelle  zu zeigen, ist folgendes Vorgehen ratsam. Zunächst einmal sind die Stetigkeit und die partielle Differenzierbarkeit der Funktion in
zu zeigen, ist folgendes Vorgehen ratsam. Zunächst einmal sind die Stetigkeit und die partielle Differenzierbarkeit der Funktion in  zu überprüfen. Denn wie gezeigt, sind diese notwendige Voraussetzungen für die totale Differenzierbarkeit. Anschließend kann mithilfe der partiellen Ableitungen die Funktionalmatrix
zu überprüfen. Denn wie gezeigt, sind diese notwendige Voraussetzungen für die totale Differenzierbarkeit. Anschließend kann mithilfe der partiellen Ableitungen die Funktionalmatrix  bestimmt werden und mit ihrer Hilfe überprüft werden, ob folgende Bedingung gilt:
bestimmt werden und mit ihrer Hilfe überprüft werden, ob folgende Bedingung gilt:

Eine alternative Formulierung dieser Bedingung lautet:

Ist diese Bedingung erfüllt, so ist  an der Stelle
an der Stelle  tatsächlich total differenzierbar.
tatsächlich total differenzierbar.
Beispiel 1: Totale Differenzierbarkeit zeigen
Wie die totale Differenzierbarkeit gezeigt werden kann, soll für folgende Funktion illustriert werden:


Da es sich um eine reellwertige Funktion handelt, kann überprüft werden, ob die partiellen Ableitungen alle stetig sind. Diese lauten:


Da beide Funktionen für alle 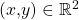 stetig sind, ist die Funktion
stetig sind, ist die Funktion  überall total differenzierbar. Dies lässt sich auch mithilfe der Bedingung
überall total differenzierbar. Dies lässt sich auch mithilfe der Bedingung

zeigen, wobei  gilt.
gilt.
Beispiel 2: Totale Differenzierbarkeit zeigen
Im folgenden Beispiel soll die totale Differenzierbarkeit im Nullpunkt  betrachtet werden:
betrachtet werden:


Es gilt:

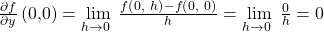
Das bedeutet, dass die Funktion im Nullpunkt partiell differenzierbar ist. Weiterhin gilt:


Somit ist die Funktion im Nullpunkt  total differenzierbar.
total differenzierbar.





 und
und  .
. ,
,