Potenzregel und Faktorregel
→
In diesem Artikel erklären wir dir, wie du mit der Potenzregel und der Faktorregel Ableitungen bestimmen kannst und rechnen viele Beispiele dazu.
Du möchtest gern alles über die Potenzregel Ableitung und die Faktorregel Ableitung erfahren, aber hast keine Lust den ganzen Artikel zu lesen? Dann schau dir einfach unser Video dazu an!
Inhaltsübersicht
Beispiel 1: positiver Exponent
Du hast die Funktion

gegeben. Da es sich hierbei um eine Potenzfunktion handelt, kannst du sie mithilfe der Potenzregel ableiten und erhältst so:

Beispiel 2: negativer Exponent
Nun hast du eine Potenzfunktion mit negativem Exponenten gegeben

und wendest erneut die Potenzregel an, um ihre Ableitung zu berechnen:

Vorsicht! Da dein Exponent negativ ist, darfst du das Minus nicht vergessen und ein Reduzieren um eins führt zu einer betraglich größeren Zahl. Das heißt dein Exponent wird noch kleiner ( ).
).
Beispiel 3: Bruch als Exponent
Diesmal steht im Exponenten von  keine ganze Zahl, sondern ein Bruch:
keine ganze Zahl, sondern ein Bruch:

Auch hier kannst du für die Ableitung einfach die Potenzregel anwenden:

Damit hast du gerade unwissentlich eine Wurzel abgeleitet. Denn du kannst  auch als Wurzel darstellen:
auch als Wurzel darstellen:

Sieh dir unseren extra Beitrag zum Wurzel Ableiten an, falls du noch mehr darüber wissen möchtest.
Tatsächlich ist die Potenzregel nicht nur für ganze und rationale Exponenten anwendbar, sondern auch allgemein für reelle. Angenommen du hast die Funktion

gegeben. Dann liefert dir die sogenannte verallgemeinerte Potenzregel die Ableitung

Im nächsten Abschnitt sehen wir uns eine weitere wichtige Ableitungsregel an, die oft im Zusammenhang mit der Potenzregel steht: die Faktorregel.
Faktorregel einfach erklärt
Angenommen du hast eine Funktion mit einem Vorfaktor gegeben und möchtest ihre Ableitung bestimmen. Dann benötigst du die Faktorregel.
f(x) = a • g(x) → f'(x)= a • g'(x)
Das bedeutet, der Vorfaktor a bleibt einfach stehen und ändert sich bei der Ableitung der Funktion nicht.
Beispiel 1
Du hast die Funktion

gegeben. In diesem Fall ist der Vorfaktor  und
und  Für die Anwendung der Faktorregel musst du die Ableitung
Für die Anwendung der Faktorregel musst du die Ableitung  berechnen. Diese erhältst du mit der Potenzregel:
berechnen. Diese erhältst du mit der Potenzregel:

Die Faktorregel liefert dir schließlich die Ableitung



Beispiel 2
Schauen wir uns ein weiteres Beispiel an

Mit der oberen Potenzregel berechnest du die Ableitung von  Das Ergebnis ist
Das Ergebnis ist

Nun wendest du die Faktorregel an und bekommst für die Ableitung


Beispiel 3: Faktorregel e Funktion
Sieh dir im Folgenden die e Funktion mit Vorfaktor  an:
an:

Für die Faktorregel musst du  ableiten und den Vorfaktor unverändert beibehalten. Die Ableitung der e Funktion
ist wieder die Funktion selbst, deshalb gilt
ableiten und den Vorfaktor unverändert beibehalten. Die Ableitung der e Funktion
ist wieder die Funktion selbst, deshalb gilt  . Damit erhältst du als Ableitung von
. Damit erhältst du als Ableitung von  :
:


Hinweis Ableitung Konstante: Falls du eine konstante Funktion  mit einer beliebigen Zahl
mit einer beliebigen Zahl  hast, so ist ihre Ableitung gleich Null:
hast, so ist ihre Ableitung gleich Null:

Du kannst dir also einfach merken, dass die Ableitung einer konstanten Funktion gleich null ist.
Potenzregel und Faktorregel — häufigste Fragen
(ausklappen)
Potenzregel und Faktorregel — häufigste Fragen
(ausklappen)-
Wie gehe ich Schritt für Schritt vor, wenn ich eine Potenzfunktion ableiten will?Du nutzt die Potenzregel: Multipliziere den Exponenten nach vorn und ziehe im Exponenten 1 ab. So wird aus
 die Ableitung
die Ableitung  . Zum Beispiel gilt bei
. Zum Beispiel gilt bei  dann
dann  .
.
-
Wie leite ich eine Funktion mit negativem Exponenten ab, ohne das Minus zu vergessen?Du wendest die Potenzregel genauso an, aber übernimmst das Minus als Teil des Exponenten. Konkret:
 wird zu
wird zu  . Achte darauf, dass „um eins reduzieren“ bei negativen Zahlen heißt:
. Achte darauf, dass „um eins reduzieren“ bei negativen Zahlen heißt:  .
.
-
Wie leite ich eine Wurzel ab, wenn sie als Bruchpotenz geschrieben ist?Du behandelst die Wurzel als Bruchpotenz und nutzt die Potenzregel. Denn
 und daraus wird
und daraus wird  . Der Bruch im Exponenten bleibt dabei erhalten, nur minus 1 wird gerechnet.
. Der Bruch im Exponenten bleibt dabei erhalten, nur minus 1 wird gerechnet.
-
Was mache ich beim Ableiten mit einem Vorfaktor vor der Funktion?Bei einem Vorfaktor nutzt du die Faktorregel: Der Vorfaktor bleibt unverändert stehen und du leitest nur den Rest ab. Aus
 wird
wird  . Beispiel:
. Beispiel:  ergibt
ergibt  .
.
-
Welche Ableitung hat eine konstante Funktion?Die Ableitung einer konstanten Funktion ist immer 0. Eine konstante Funktion bedeutet, dass
 für alle
für alle  gleich bleibt und sich nicht verändert. Deshalb gilt direkt:
gleich bleibt und sich nicht verändert. Deshalb gilt direkt:  .
.
Weitere Ableitungsregeln
Neben der Potenzregel und der Faktorregel gibt es natürlich noch weitere wichtige Ableitungsregeln, die du kennen solltest:
| Ableitungsregel | Funktion | Ableitung |
| Summenregel |  |
 |
| Differenzregel |  |
 |
| Produktregel |  |
 |
| Quotientenregel |  |
![Rendered by QuickLaTeX.com f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1128d60300515aa8b8df5c88d4dbbdf9_l3.png) |
| Kettenregel |  |
 |
| Potenzregel |  |
 |
| Faktorregel | 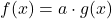 |
 |