Kurvenintegral
In diesem Artikel wollen wir dir vor allem zeigen, was ein Kurvenintegral ist und wie du es berechnen kannst. Als Grundlage hierfür erläutern wir zunächst die Begriffe Weg und Kurve. Außerdem erklären wir dir, wie man zur Berechnungsformel von Kurvenintegralen gelangt und gehen auf wichtige Eigenschaften von Kurvenintegralen ein. Zwei Berechnungsbeispiele dienen der Veranschaulichung der theoretischen Überlegungen.
Noch anschaulicher und einprägsamer ist unser Video zum Thema Kurvenintegral.
Inhaltsübersicht
Kurvenintegral einfach erklärt
Aus der Schule ist dir sicher das gewöhnliche Integral über eine Funktion  bekannt.
bekannt.

Die Definitionsmenge der Funktion  ist eine Teilmenge der reellen Zahlen. Zur Berechnung des Integrals kannst du dir vorstellen, dass du alle Funktionswerte zwischen den Grenzen
ist eine Teilmenge der reellen Zahlen. Zur Berechnung des Integrals kannst du dir vorstellen, dass du alle Funktionswerte zwischen den Grenzen  und
und  aufsummierst.
aufsummierst.
Man kann allerdings auch über Funktionen integrieren, die eine Teilmenge  des
des  als Definitionsmenge besitzen.
als Definitionsmenge besitzen.
Hier können aber nicht einfach zwei Integralgrenzen angegeben werden. Stattdessen muss eine Teilmenge von  als Integrationsbereich angegeben werden. Falls man hierfür eine sogenannte Kurve
als Integrationsbereich angegeben werden. Falls man hierfür eine sogenannte Kurve  auswählt, so heißt das betrachtete Integral Kurvenintegral.
auswählt, so heißt das betrachtete Integral Kurvenintegral.

Beispielsweise kann der Definitionsbereich der ganze  sein und die betrachtete Kurve ein Kreis in der Ebene sein. Dann kannst du dir vorstellen, dass zur Berechnung des Kurvenintegrals alle Funktionswerte entlang des Kreises aufsummiert werden müssen.
sein und die betrachtete Kurve ein Kreis in der Ebene sein. Dann kannst du dir vorstellen, dass zur Berechnung des Kurvenintegrals alle Funktionswerte entlang des Kreises aufsummiert werden müssen.
Weg
Ein Weg  ist eine stetige Abbildung eines reellen Intervalls
ist eine stetige Abbildung eines reellen Intervalls ![Rendered by QuickLaTeX.com I=[a,b]\subset\mathbb{R}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-70d841fba771d2627baa6537cf2328c3_l3.png) in den
in den  mit
mit  :
:

Dabei nennt man das Bild ![Rendered by QuickLaTeX.com \gamma\left([a,b]\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-67f65d251ccff3c20d69df066d94a094_l3.png) die Spur des Weges und die Abbildungsvorschrift heißt Parametrisierung des Weges. Die folgenden beiden Wege besitzen die selbe Spur.
die Spur des Weges und die Abbildungsvorschrift heißt Parametrisierung des Weges. Die folgenden beiden Wege besitzen die selbe Spur.
![Rendered by QuickLaTeX.com \gamma_1: [-1,1]\rightarrow \mathbb{R}^2,\,\,\,t\mapsto\left(\begin{array}{cc}t\\\sqrt{1-t^2}\end{array}\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-479bf5458bcc6f9605934177685982eb_l3.png)
![Rendered by QuickLaTeX.com \gamma_2: [0,\pi]\rightarrow \mathbb{R}^2,\,\,\,t\mapsto\left(\begin{array}{cc}\cos (t)\\\sin (t)\end{array}\right)](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-46ab7e243f8af475bc9aab023bff955e_l3.png)
Sie stellt den Einheitshalbkreis in der oberen Halbebene dar.
Kurve
Die Spur eines Weges wird als Kurve bezeichnet. Somit stellen  und
und  die Parametrisierung der gleichen Kurve dar.
die Parametrisierung der gleichen Kurve dar.
Kurvenintegral 1. Art
Kurvenintegrale 1. Art sind Kurvenintegrale einer skalaren Funktion  . Eine solche Funktion wird auch Skalarfeld genannt. Sie ordnet jedem Wert
. Eine solche Funktion wird auch Skalarfeld genannt. Sie ordnet jedem Wert  eine reelle Zahl
eine reelle Zahl  zu.
zu.
Ist die Teilmenge  offen und
offen und ![Rendered by QuickLaTeX.com \gamma:[a,b]\rightarrow \mathbb{R}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a6012a63f9060ef89fbb4daeda0beac9_l3.png) die Parametrisierung einer stückweise stetig differenzierbaren Kurve. Dann heißt
die Parametrisierung einer stückweise stetig differenzierbaren Kurve. Dann heißt

das Kurvenintegral 1. Art von  längs der Kurve
längs der Kurve  . Häufig wird für ein Kurvenintegral auch der Begriff des Linienintegrals verwendet. Auch der Begriff Wegintegral ist hierfür üblich. Allerdings können verschiedene Wege möglicherweise auch nur unterschiedliche Parametrisierungen ein und derselben Kurve beschreiben, wie oben bereits dargelegt wurde.
. Häufig wird für ein Kurvenintegral auch der Begriff des Linienintegrals verwendet. Auch der Begriff Wegintegral ist hierfür üblich. Allerdings können verschiedene Wege möglicherweise auch nur unterschiedliche Parametrisierungen ein und derselben Kurve beschreiben, wie oben bereits dargelegt wurde.
Anschauliche Deutung bzw. Herleitung
Aus der Schule dürfte die Deutung von Integralen als Summe über unendlich feine Rechtecke bekannt sein. Dabei stellt der Funktionswert an der betrachteten Stelle die Höhe eines solchen Rechtecks dar. Der Breite des Rechtecks entspricht eine kleine Strecke des Bereichs über den integriert wird. Beim Kurven- oder Linienintegral ist dieser Bereich eben eine Kurve. Diese wird mithilfe der Variablen  parametrisiert, die zwischen den Grenzen
parametrisiert, die zwischen den Grenzen  und
und  läuft. Nun wollen wir versuchen, die Länge eines kleinen Kurvenstücks näherungsweise zu bestimmen. Dazu teilen wir das Parametrisierungsintervall in
läuft. Nun wollen wir versuchen, die Länge eines kleinen Kurvenstücks näherungsweise zu bestimmen. Dazu teilen wir das Parametrisierungsintervall in  Stücke ein:
Stücke ein:

Um die Länge des Kurvenstücks zwischen  und
und  zu nähern, betrachten wir einfach die Länge der Geraden
zu nähern, betrachten wir einfach die Länge der Geraden 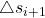 durch diese zwei Punkte:
durch diese zwei Punkte:

Nun lässt sich diese Gleichung nach dem Mittelwertsatz der Differentialrechnung auch folgendermaßen ausdrücken:

Hierbei gilt  .
.
Bildet man nun über all diese kleinen Kurvenstücke die Riemann-Summe und geht über zu einer unendlich feinen Zerlegung ( und
und  ), so erhält man das Kurvenintegral 1. Art.
), so erhält man das Kurvenintegral 1. Art.

Kurvenintegral berechnen 1. Art
Zur Berechnung eines Kurvenintegrals 1. Art  kann man sich folgende Vorgehensweise merken:
kann man sich folgende Vorgehensweise merken:
- Die Kurve
 parametrisieren und in
parametrisieren und in  einsetzen
einsetzen
– mit
mit 
–
- Das skalare Bogenelement
 bestimmen
bestimmen - In das Integral
 mit den Grenzen
mit den Grenzen  und
und  einsetzen und ausrechnen
einsetzen und ausrechnen
Kurvenintegral Beispiel 1. Art
Das eben beschriebene Vorgehen, mit dem man ein Kurvenintegral berechnen kann, soll nun an einem Beispiel verdeutlicht werden. Hierzu wollen wir das Kurven- bzw. Linienintegral der Funktion  entlang des Kreises um den Ursprung mir Radius
entlang des Kreises um den Ursprung mir Radius  berechnen.
berechnen.
Kurvenintegral Kreis:
-
Kreis parametrisieren:
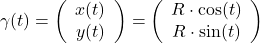 mit
mit 
In einsetzen:
einsetzen: 
-
Bogenelement berechnen:

- Mit den Grenzen
 und
und  einsetzen und berechnen:
einsetzen und berechnen: 
Kurvenintegral 2. Art
Beim Kurvenintegral 1. Art haben wir über eine skalarwertige Funktion integriert. Beim Kurvenintegral 2. Art integriert man nun über eine vektorwertige Funktion. Eine solche Funktion wird auch Vektorfeld genannt. Sie bildet von einer Teilmenge  des
des  in den
in den  ab.
ab.

Für ein solches stetiges Vektorfeld und eine stückweise stetig differenzierbare Kurve  heißt
heißt

das Kurvenintegral 2. Art von  längs der Kurve
längs der Kurve  .
.
Kurvenintegral berechnen 2. Art
Falls man ein Kurvenintegral 2. Art berechnen will, bietet sich folgende Vorgehensweise an.
- Die Kurve
 parametrisieren und in
parametrisieren und in  einsetzen
einsetzen
– mit
mit 
–
- Das vektorielle Bogenelement
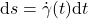 bestimmen
bestimmen - In das Integral
 mit den Grenzen
mit den Grenzen  und
und  einsetzen und ausrechnen
einsetzen und ausrechnen
Kurvenintegral Beispiel 2. Art
Auch für das Kurvenintegral 2. Art wollen wir an dieser Stelle eine Besipielrechnung angeben.
Wir betrachten die Funktion
 .
.
Diese soll entlang der Kurve mit der Parametrisierung
 mit
mit 
integriert werden.
- Da die Parametrisierung bereits gegeben ist, müssen wir diese nur noch in die Funktion einsetzen:

- Nun berechnen wir das vektorielle Bogenelement:

- Zuletzt setzen wir diese Ergebnisse mit den Grenzen
 und
und  in
in  ein:
ein:

Eigenschaften des Kurvenintegrals
Im folgenden sollen noch ein paar wichtige Infos zu Kurvenintegralen gegeben werden.
1. Hauptsatz für Kurvenintegrale
Falls zu dem Vektorfeld  eine Funktion
eine Funktion  existiert, sodass
existiert, sodass  der Gradient
von
der Gradient
von  ist, so nennt man
ist, so nennt man  ein Gradientenfeld oder konservativ.
ein Gradientenfeld oder konservativ.

Ist  ein Gradientenfeld auf dem Gebiet
ein Gradientenfeld auf dem Gebiet  mit einer Stammfunktion
mit einer Stammfunktion  , so gilt für jede stückweise stetig differenzierbare Kurve
, so gilt für jede stückweise stetig differenzierbare Kurve  in
in  , mit dem Startpunkt
, mit dem Startpunkt  und dem Endpunkt
und dem Endpunkt 

Das heißt, dass das Kurvenintegral über Gradientenfelder nur vom Start- und Endpunkt der Kurve abhängt. Der genaue Verlauf der Kurve ist irrelevant.
Rechenregeln
Wenn  und
und  gleicher Art sind,
gleicher Art sind,  und
und  Urbilder gleicher Dimension besitzen und
Urbilder gleicher Dimension besitzen und ![Rendered by QuickLaTeX.com \gamma: [a,b]\rightarrow \mathbb{R}^n](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3f525c0335a7178572b4a9dbcd26e091_l3.png) ist, dann gilt:
ist, dann gilt:
-
 für
für  (Linearität)
(Linearität)
-
![Rendered by QuickLaTeX.com \int\limits_{\gamma}f\mathrm{d}s=\int\limits_{\gamma\vert_{[a,c]}}f\mathrm{d}s+\int\limits_{\gamma\vert_{[c,b]}}f\mathrm{d}s](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-dbd47dca0406016936e81d85800b35db_l3.png) für
für ![Rendered by QuickLaTeX.com c\in [a,b]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-18f5c7d157452603cbffdd3045f6b40e_l3.png) (Zerlegungsadditivität)
(Zerlegungsadditivität)
Kurvenintegrale über geschlossene Kurven
Falls die Kurve, entlang der man integrieren soll, geschlossen ist, wird das durch einen Kreis im Integralzeichen verdeutlicht. Also kann man für geschlossene Kurven statt  auch
auch  schreiben. Ist das Vektorfeld ein Gradientenfeld, so ist das Integral entlang einer geschlossenen Kurve stets Null. Das ergibt sich direkt aus dem 1. Hauptsatz für Kurvenintegrale.
schreiben. Ist das Vektorfeld ein Gradientenfeld, so ist das Integral entlang einer geschlossenen Kurve stets Null. Das ergibt sich direkt aus dem 1. Hauptsatz für Kurvenintegrale.
Komplexes Kurvenintegral
Der Begriff des Kurvenintegrals lässt sich auch auf das Komplexe übertragen:
Sei  ein Gebiet,
ein Gebiet,  stetig und
stetig und ![Rendered by QuickLaTeX.com \gamma:[a,b]\rightarrow D](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-31a5fd608be4f9215620a06a8b1c29ff_l3.png) ein stückweise stetig differenzierbarer Weg. Dann ist
ein stückweise stetig differenzierbarer Weg. Dann ist

das komplexe Kurvenintegral von  entlang der von
entlang der von  beschriebenen Kurve.
beschriebenen Kurve.