Ganzrationale Funktionen
In diesem Artikel erklären wir dir alles Wichtige zum Thema ganzrationale Funktionen, die manchmal auch Polynomfunktion heißen. Dabei gehen wir anhand ausgewählter Beispiele auf ihre verschiedenen Eigenschaften, Nullstellen und Grenzwerte ein. Am Ende des Textes findest du zudem einige Aufgaben zum selbst Üben.
Um ganzrationale Funktionen noch besser zu verstehen, schau dir unser Video an! Hier findest du alles Wichtige direkt am Beispiel erklärt!
Inhaltsübersicht
Ganzrationale Funktionen einfach erklärt
Ganzrationale Funktionen oder Polynomfunktionen, werden stets in Abgrenzung zu den gebrochen rationalen Funktionen
definiert. Polynomfunktionen sind – wie der Name bereits sagt – immer die Summe einzelner polynomieller Bestandteile in einer Variablen  .
.

Je nachdem, welche Werte du für  und für
und für 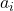 mit
mit  einsetzt, erhältst du verschiedene Polynomfunktionen beziehungsweise ganzrationale Funktionen mit unterschiedlichen Funktionsgraphen.
einsetzt, erhältst du verschiedene Polynomfunktionen beziehungsweise ganzrationale Funktionen mit unterschiedlichen Funktionsgraphen.
Was ist eine ganzrationale Funktion?
Bei Polynomfunktionen gibt es verschiedene Begriffe, die du kennen solltest. Betrachten wir dazu den lila Graphen aus obiger Abbildung mit der Funktionsgleichung
 .
.
Der ganze Ausdruck wird als ganzrationale Funktion beziehungsweise Polynomfunktion 4. Grades bezeichnet, da der höchste Exponent  ist. Manchmal spricht man auch von einem Polynom
der Ordnung 4. Dieser höchste Exponent entscheidet, wie die Funktion global betrachtet aussieht, und wie sie sich an den Rändern des Definitionsbereichs
verhält. Die Faktoren vor den Potenzen, das heißt in diesem Falle
ist. Manchmal spricht man auch von einem Polynom
der Ordnung 4. Dieser höchste Exponent entscheidet, wie die Funktion global betrachtet aussieht, und wie sie sich an den Rändern des Definitionsbereichs
verhält. Die Faktoren vor den Potenzen, das heißt in diesem Falle  ,
,  ,
,  ,
,  und
und  werden Koeffizienten genannt, der Faktor vor der höchsten Potenz (hier
werden Koeffizienten genannt, der Faktor vor der höchsten Potenz (hier  ) heißt Leitkoeffizient.
) heißt Leitkoeffizient.
Merke: Ganzrationale Funktionen, die nur aus dem Leitkoeffizienten und einer Potenz bestehen, werden auch Potenzfunktionen genannt!
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Konstante Funktion
Konstante Funktionen bezeichnet man oft als Polynomfunktion 0. Grades, weil sie unabhängig von x sind. Diese Benennung ist deshalb sinnvoll, da für alle x-Werte x0=1 ist. Die wichtigsten Eigenschaften zusammengefasst lauten:
- allgemeine Funktionsgleichung: f(x)=c
- Funktionsgraph: waagrechte Gerade, die die y-Achse bei c schneidet
- Beispiel: f(x)=2 mit Leitkoeffizient a0=2
Lineare Funktion
Lineare Funktionen entsprechen den ganzrationalen Funktionen 1. Grades. Hier ist nur eine x-Variable in ihrer ersten Potenz enthalten, das heißt x1 =x. Die wichtigsten Eigenschaften lauten zusammengefasst:
- allgemeine Funktionsgleichung: f(x)= mx+b
- Funktionsgraph: Gerade mit Steigung m und y-Achsenabschnitt b
- Beispiel: f(x)=0,5x+3 mit Steigung m=a1=0,5 und y-Achsenabschnitt b=a0=3
Quadratische Funktion
Quadratische Funktionen werden auch als Polynomfunktionen vom Grad 2 bezeichnet. Sie beschreiben die Parabeln im Koordinatensystem. Zusammengefasst gilt hier:
- allgemeine Funktionsgleichung: f(x)=ax2+bx+c oder Scheitelpunktform : f(x)=a(x-d)2+e
- Funktionsgraph: Parabel
- Beispiel: f(x)=-x2+2x-1 mit Leitkoeffizient a=a_2=-1, b=a1=2 und c=a0=-1
Kubische Funktion
Eine ganzrationale Funktion 3. Grades wird kubische Funktion genannt. Hier lassen sich die wichtigsten Punkte wie folgt zusammenfassen:
- allgemeine Funktionsgleichung: f(x)=a3x3+a2x2+a1x+a0
- Funktionsgraph: Parabelähnlicher Graph vom Grad 3
- Beispiel: f(x)=2x3-4x2+3x-1
Ganzrationale Funktion 4. Grades
Zuletzt wollen wir noch die ganzrationalen Funktionen vom Grad 4 betrachten. Diese haben keinen besonderen Namen mehr.
- allgemeine Funktionsgleichung: f(x)=a4x4+a3x3+a2x2+a1x+a0
- Funktionsgraph: Parabelähnlicher Graph vom Grad 4
- Beispiel: f(x)=x4-x3-2x2+3x+5
Ganzrationale Funktionen: Beispiele und Nichtbeispiele
Einige Beispiele hast du im vorherigen Kapitel bereits gesehen. Jetzt fragst du dich vielleicht, inwiefern sich Polynomfunktionen von Nicht-Polynomfunktionen unterscheiden.
Einige weitere Beispiele für ganzrationale Funktionen sind
Keine Polynomfunktionen sind im Gegensatz dazu
-
Exponentialfunktionen
der Form

-
Wurzelfunktionen
![Rendered by QuickLaTeX.com f(x)=\sqrt[n]{x}](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a954f5d2d63ea38aeda8c82fb4cc8dfe_l3.png)
- trigonometrische Funktionen f(x)= sin(x)
-
gebrochen rationale Funktionen

Symmetrie
Eine Funktion heißt achsensymmetrisch, wenn gilt
f(x)=f(-x).
Damit sind ganzrationale Funktionen genau dann achsensymmetrisch zur x-Achse, wenn sie nur gerade Exponenten enthalten. An einem Beispiel siehst du direkt, dass sich hier die negativen Vorzeichen alle gegenseitig aufheben.

Enthalten ganzrationale Funktionen dahingegen nur ungerade Exponenten, so sind sie punktsymmetrisch zum Ursprung, das heißt
f(-x)=-f(x).
Auch hier siehst du das direkt am Beispiel der Polynomfunktion  :
:

Merke: Enthält eine Polynomfunktion sowohl gerade als auch ungerade Exponenten, so ist sie weder punktsymmetrisch noch achsensymmetrisch! Das siehst du auch direkt in obiger Abbildung!
Grenzwerte
Auch die Grenzwerte verschiedener Polynomfunktionen unterscheiden sich, je nach Grad der ganzrationalen Funktion und Vorzeichen des Leitkoeffizienten  .
.
Gerader Grad
Ganzrationale Funktionen mit geradem Exponenten ähneln global betrachtet einer quadratischen Funktion. Sie können zwar verschiedene Extremstellen und mehrere lokale Minima und Maxima besitzen, letzten Endes laufen die beiden Parabel-Äste aber in die gleiche Richtung. Dabei gibt es zwei Möglichkeiten:
- Der Leitkoeffizient hat ein positives Vorzeichen: Dann ist die Parabel nach oben geöffnet
 und
und  .
.
- Der Leitkoeffizient hat ein negatives Vorzeichen: Hier ist die Parabel nach unten geöffnet
 und
und  .
.
Ungerader Grad
Für ganzrationale Funktionen mit ungeradem Grad ergibt sich ein anderes Bild. Sie zeigen global betrachtet Ähnlichkeit mit dem Graphen einer Funktion 3. Grades, wobei auch hier das Vorzeichen des Leitkoeffizienten  über das Verhalten im Unendlichen bestimmt:
über das Verhalten im Unendlichen bestimmt:
- Der Leitkoeffizient hat ein positives Vorzeichen
 und
und  .
.
- Der Leitkoeffizient hat ein negatives Vorzeichen
 und
und  .
.
Nullstellen berechnen
Um die Nullstellen einer Polynomfunktion zu berechnen, gibt es verschiedene Möglichkeiten, abhängig vom Grad den die ganzrationale Funktion hat. Allgemein berechnest du immer
f(x)=0.
Für lineare Funktionen kann man diesen Term einfach auflösen, bei den quadratischen Termen hilft die Mitternachtsformel oder die pq-Formel weiter. Bei Polynomfunktionen mit höherer Ordnung gibt es hingegen keine einfachen Lösungsformeln mehr, hier kann man entweder Ausklammern oder eine Polynomdivision durchführen – sofern eine Nullstelle bekannt ist. Das genaue Vorgehen erklären wir dir für jeden Funktionstyp einzeln im separaten Video Nullstellen berechnen .
Im Allgemeinen gilt jedoch, dass die Anzahl der reellen Nullstellen einer Polynomfunktion kleiner gleich dem Grad der Polynomfunktion ist. Das heißt, dass zum Beispiel eine ganzrationale Funktion vom Grad 5 höchstens 5 Nullstellen besitzen kann.
Extrema
Ganzrationale Funktionen haben meist mehrere (lokale) Extrempunkte, beispielsweise Minima, Maxima oder Sattelpunkte. Um sie zu bestimmen, gehst du wie folgt vor:
- Schritt 1: Berechne zuerst die Ableitung der Polynomfunktion und verwende dazu die Faktor- und Potenzregeln.
- Schritt 2: Berechne die Nullstellen der Ableitung. Das sind die x-Koordinaten der Extrempunkte.
- Schritt 3: Bestimme die zugehörige y-Koordinate durch Einsetzen in die ursprüngliche Funktion.
- Schritt 4: Bestimme die Art der Extrempunkte: Maximum, Minimum oder Sattelpunkt?
Allgemein ist die Ableitung  für ganzrationale Funktionen
für ganzrationale Funktionen  vom Grad
vom Grad  immer eine Polynomfunktion vom Grad
immer eine Polynomfunktion vom Grad  . Das bedeutet gleichzeitig, dass eine Polynomfunktion vom Grad
. Das bedeutet gleichzeitig, dass eine Polynomfunktion vom Grad  maximal
maximal  Extrempunkte besitzen kann.
Extrempunkte besitzen kann.
Ganzrationale Funktionen Aufgaben
Im Folgenden zeigen wir dir verschiedene Aufgaben mit Lösungen zum Thema ganzrationale Funktionen.
Aufgabe 1: Bestimme die Funktionsgleichung für ganzrationale Funktionen
a) Gesucht ist eine ganzrationale Funktion 3. Grades, die eine einfache Nullstelle im Ursprung besitzt und eine doppelte Nullstelle bei x=4.
b) Gesucht ist eine ganzrationale Funktion 4. Grades, die eine doppelte Nullstelle bei x=2 besitzt, durch den Punkt P(0|4) verläuft und symmetrisch zur y-Achse ist. Überlege dir zuerst, wie der Funktionsgraph aussehen muss.
Aufgabe 2: Kurvendiskussion für ganzrationale Funktionen
Gegeben ist die ganzrationale Funktion  .
.
a) Welchen Grad hat die Polynomfunktion? Bestimme auch ihren Leitkoeffizienten.
b) Bestimme alle Nullstellen der Funktion.
c) Wie verhält sich die ganzrationale Funktion an den Rändern ihres Definitionsbereichs?
d) Berechne alle Extrempunkte der Polynomfunktion.
e) Zeichne die ganzrationale Funktion.
Lösungen
Aufgabe 1: Bestimme die Funktionsgleichung für ganzrationale Funktionen
a) Am einfachsten kannst du die gesuchte Gleichung der Polynomfunktion bestimmen, wenn du sie in faktorisierter Form aufschreibst. Da f(x) eine einfache Nullstelle bei x=0 und eine doppelte Nullstelle bei x=4 hat, ist die Funktionsgleichung

b) Hier ist eine ganzrationale Funktion 4. Grades gesucht, die eine doppelte Nullstelle bei x=2 haben soll. Ihre faktorisierte Form enthält somit in jedem Fall den Faktor  . Da die Funktion symmetrisch zur y-Achse sein soll, muss sie auch eine doppelte Nullstelle bei x=-2 haben, das heißt den Faktor
. Da die Funktion symmetrisch zur y-Achse sein soll, muss sie auch eine doppelte Nullstelle bei x=-2 haben, das heißt den Faktor  enthalten. Wir erhalten also die Gleichung
enthalten. Wir erhalten also die Gleichung

Diese ganzrationale Funktion verläuft aber noch nicht durch den Punkt  , wir müssen sie daher noch entsprechend strecken beziehungsweise stauchen. Das entspricht der Bestimmung des Leitkoeffizienten, wozu wir den Punkt P in die Funktionsgleichung einsetzen:
, wir müssen sie daher noch entsprechend strecken beziehungsweise stauchen. Das entspricht der Bestimmung des Leitkoeffizienten, wozu wir den Punkt P in die Funktionsgleichung einsetzen:

Diese Gleichung lässt sich mit  lösen und liefert die Funktionsgleichung
lösen und liefert die Funktionsgleichung
 .
.
Aufgabe 2: Kurvendiskussion für ganzrationale Funktionen
a) Die ganzrationale Funktion  ist eine Polynomfunktion vom Grad 3. Ihr Leitkoeffizient ist
ist eine Polynomfunktion vom Grad 3. Ihr Leitkoeffizient ist  .
.
b) Um die Nullstelle zu berechnen, kann man  direkt ausklammern
direkt ausklammern

Damit ist  und wir müssen nur noch die Nullstellen der quadratischen Polynomfunktion
und wir müssen nur noch die Nullstellen der quadratischen Polynomfunktion  berechnen.
berechnen.

Die Polynomfunktion hat also die einfache Nullstelle  und eine doppelte Nullstelle bei
und eine doppelte Nullstelle bei  .
.
c) Die Polynomfunktion hat die beiden Limiten 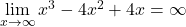 und
und  .
.
d) Um die Extrempunkte zu bestimmen, berechnen wir die Nullstellen der Ableitung.


Bei  hat die Polynomfunktion ein lokales Maximum, bei
hat die Polynomfunktion ein lokales Maximum, bei  ein lokales Minimum.
ein lokales Minimum.
e) Der Funktionsgraph der Polynomfunktion sieht folgendermaßen aus:
Ganzrationale Funktionen — häufigste Fragen
(ausklappen)
Ganzrationale Funktionen — häufigste Fragen
(ausklappen)-
Was macht eine Funktion zu einer ganzrationalen Funktion?Eine ganzrationale Funktion ist eine Summe von Termen der Form
 mit ganzzahligen Exponenten. Dabei kommt nur die Variable x vor, und es gibt keinen Bruchterm mit x im Nenner. Allgemein schreibt man sie als
mit ganzzahligen Exponenten. Dabei kommt nur die Variable x vor, und es gibt keinen Bruchterm mit x im Nenner. Allgemein schreibt man sie als  .
.
-
Wie erkenne ich den Grad und den Leitkoeffizienten bei einer ganzrationalen Funktion?Den Grad erkennst du am höchsten Exponenten, der in der Funktion vorkommt. Der Leitkoeffizient ist die Zahl vor dem Term mit diesem höchsten Exponenten. Bei
 ist der Grad 4 und der Leitkoeffizient
ist der Grad 4 und der Leitkoeffizient  .
.
-
Welche Funktionen zählen nicht zu den ganzrationalen Funktionen?Nicht ganzrational sind Funktionen, die keine Summe aus Potenzen
 mit ganzzahligen Exponenten sind. Dazu gehören Exponentialfunktionen wie
mit ganzzahligen Exponenten sind. Dazu gehören Exponentialfunktionen wie  , Wurzelfunktionen wie
, Wurzelfunktionen wie ![Rendered by QuickLaTeX.com f(x)=\sqrt[n]{x}](https://blog.studyflix.de/wp-content/ql-cache/quicklatex.com-a954f5d2d63ea38aeda8c82fb4cc8dfe_l3.png) und trigonometrische Funktionen wie
und trigonometrische Funktionen wie  . Auch gebrochen rationale Funktionen wie
. Auch gebrochen rationale Funktionen wie  gehören nicht dazu.
gehören nicht dazu.
-
Wie berechne ich die Nullstellen einer ganzrationalen Funktion?Nullstellen findest du, indem du
 setzt und nach x auflöst. Bei linearen Funktionen kannst du direkt umformen, bei quadratischen nutzt du die Mitternachtsformel oder die pq-Formel. Bei höheren Graden klappt oft Ausklammern oder Polynomdivision, wenn schon eine Nullstelle bekannt ist.
setzt und nach x auflöst. Bei linearen Funktionen kannst du direkt umformen, bei quadratischen nutzt du die Mitternachtsformel oder die pq-Formel. Bei höheren Graden klappt oft Ausklammern oder Polynomdivision, wenn schon eine Nullstelle bekannt ist.
-
Wie finde ich Extrempunkte bei einer ganzrationalen Funktion?Extrempunkte findest du über die Ableitung: Erst berechnest du
 mit Potenzregel und Faktorregel. Dann löst du
mit Potenzregel und Faktorregel. Dann löst du  , das sind die x-Koordinaten der Extrempunkte. Danach setzt du diese x-Werte in
, das sind die x-Koordinaten der Extrempunkte. Danach setzt du diese x-Werte in  ein, um die y-Koordinaten zu bekommen, und bestimmst die Art des Punkts.
ein, um die y-Koordinaten zu bekommen, und bestimmst die Art des Punkts.
Gebrochen rationale Funktionen
Neben den ganzrationalen Funktionen gibt es auch noch die gebrochen rationalen Funktionen. Sie haben als Funktionsterm einen Bruch aus zwei Polynomen. In unserem Video dazu erfährst alles Wichtige, das du zu den gebrochen rationalen Funktionen wissen musst. Schau es dir gleich an!












