Isobare Zustandsänderung
Die isobare Zustandsänderung gehört zu den wichtigsten Zustandsänderungen der Thermodynamik. Wir untersuchen, welche Zustandsgröße konstant bleibt und wie die Zustandskurven aussehen. In unseren anderen Beiträgen erhältst du alle wichtigen Informationen über die isotherme , isochore und die adiabatische Zustandsänderung .
„isobar“ ist griechisch und bedeutet „gleicher Druck“. Das beschreibt exakt welche Zustandsgröße konstant bleibt: Der Druck. Die Temperatur und das Volumen verändern sich hingegen. Damit der Druck konstant bleibt, muss gleichzeitig Arbeit in Form von Volumenarbeit und ein Wärmetransport stattfinden.
Inhaltsübersicht
Isobare Expansion und Kompression
Wenn wir zum Beispiel dem System Wärme Q zuführen, dann muss das Gas Volumenarbeit verrichten, um den Druck konstant zu halten. Das Volumen und auch die innere Energie steigen daher. Diesen Vorgang kennt man auch unter dem Namen „isobare Expansion“.
Verringern sich das Volumen V und die innere Energie U, dann spricht man von „isobarer Kompression“.
Für einen konstanten Druck im System ergibt sich aus dem idealen Gasgesetz:

Dieser Zusammenhang zwischen Volumen und Temperatur bei einer isobaren Zustandsänderung wird durch das Gesetz von Gay-Lussac beschrieben.
Wollen wir nun aus den Zustandsgrößen des ersten Zustands eine Zustandsgröße des zweiten Zustands berechnen, dann müssen wir die Formel

nur nach der gewünschten Größe umstellen.
Sind die Anfangs- und Endtemperaturen gegeben, können wir daraus die Änderung der inneren Energie  bei einer isobaren Zustandsänderung ermitteln:
bei einer isobaren Zustandsänderung ermitteln:

- m = Gasmasse
-
 = spezifische Wärmekapazität des Gases
= spezifische Wärmekapazität des Gases
Thermische Zustandsgleichung
Die thermische Zustandsgleichung für alle idealen Gase gibt die Beziehungen zwischen den thermischen Zustandsgrößen an. Wir können Sie zur Untersuchung thermodynamischer Prozesse zu Hilfe nehmen. Die Formel lautet:

-
 = universelle/molare Gaskonstante
= universelle/molare Gaskonstante -
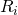 = individuelle/spezifische Gaskonstante
= individuelle/spezifische Gaskonstante
Bei der isobaren Zustandsänderung gilt p = konst., weswegen die zwei Zustandsgleichungen gelten:


Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
p-V- und T-s-Diagramm
Betrachten wir nun das p-V-Diagramm und das T-s-Diagramm .
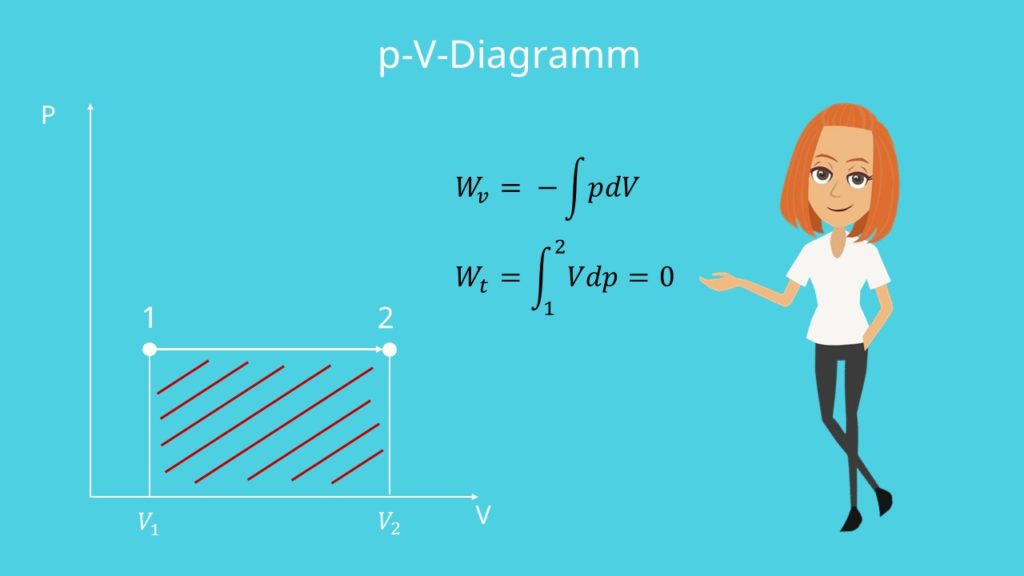
Die Zustandskurve verläuft im p-V-Diagramm horizontal bzw. parallel zur V-Achse. Klar, der Druck ist bei isobaren Zustandsänderungen ja konstant.
Die Fläche unterhalb der Zustandskurve entspricht der verrichteten Volumenänderungsarbeit  .
.
Im T-s-Diagramm stellt sich ein exponentieller Verlauf ein, allerdings mit einer geringeren Steigung als bei einer isochoren Zustandsänderung. Die Fläche unter der Kurve entspricht der zugeführten bzw. abgeführten Wärmeenergie.
Berechnung der Volumenarbeit
Wie wir bereits gesehen haben, lautet die Formel für die Änderung der inneren Energie in einem geschlossenen System:

Bei der isobaren Zustandsänderung bleibt der Druck p konstant, was Einfluss auf die Formel der Volumenänderungsarbeit hat:

Daraus folgt:

Durch Umformung mit Hilfe der thermischen Zustandsgleichung erhalten wir:

Druckänderungsarbeit
Der Druck bei der isobaren Zustandsänderung bleibt konstant, weswegen die reversible technische Arbeit, auch Druckänderungsarbeit genannt, gleich null ist.
Mathematisch können wir Sie wie folgt ausdrücken:

Im p-V-Diagramm entspricht die Druckänderungsarbeit der Fläche unter der Zustandskurve zur p-Achse hin, die gleich null ist.
Wärme
Wollen wir die zu- bzw. abgeführte Wärme ermitteln, müssen wir die Formel der Enthalpie heranziehen:
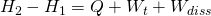
Lösen wir die Gleichung nach der Wärme Q auf und berücksichtigen, dass die Druckänderungsarbeit gleich null ist, erhalten wir schließlich für die Wärme:
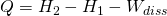
Handelt es sich um einen reversiblen Prozess fällt der Ausdruck für die Dissipationsarbeit weg.
Die Wärme Q entspricht der Fläche unter der Zustandskurve im T-s-Diagramm.
Entropie
Die Entropie in einem System ist abhängig von der Wärme und im Falle der isobaren Zustandsänderung können wir die Formel auch in Abhängigkeit zur Enthalpie formulieren:

Da der Druck konstant bleibt, fällt der Ausdruck  weg:
weg:

-
 = spezifische Wärmekapazität
= spezifische Wärmekapazität
Wir können die Entropie auch in einem T-s-Diagramm darstellen. Sie lässt sich auch über folgende Beziehung ausdrücken:

Die Fläche unter der Zustandskurve im T-s- Diagramm entspricht dabei der Summe aus der Wärme und der Dissipationsarbeit.
Fassen wir kurz zusammen, was wir gelernt haben. Bei der isobaren Zustandsänderung bleibt der Druck konstant. Daher ist die Zustandskurve im p-V-Diagramm eine Gerade. Es wird gleichzeitig Volumenarbeit verrichtet und Wärmeenergie transportiert.