Polytrope Zustandsänderung
Die polytrope Zustandsänderung ist sehr aufschlussreich für uns, da sich aus ihr alle Zustandsänderungen ableiten lassen, die wir kennen. Gucken wir uns das genauer an!
Inhaltsübersicht
Polytrope Zustandsänderungen im pV Diagramm
Betrachten wir nochmal die isobare , isochore , isotherme und isentrope Zustandsänderung im p-V-Diagramm , dann sehen wir, dass die Kurvenverläufe alle unterschiedlich aussehen. Mit der Formel der polytropen Zustandsänderungen können wir alle Linien ableiten. Diese lautet:

Betrachten wir das p-V-Diagramm einmal genauer.
Die isotherme Zustandsänderung tritt nur ein, wenn die zu- beziehungsweise abgeführte Arbeit wieder als Wärme ab- beziehungsweise zugeführt wird. Dieser Grenzfall liegt nur bei sehr langsam ablaufenden Prozessen vor.
Die isentrope Zustandsänderung tritt nur ein, wenn keine Wärme zu- oder abgeführt wird. Das ist bei sehr schnell ablaufenden Prozessen der Fall.
Beide Grenzfälle werden in der Realität nicht vollständig erreicht, wodurch sich die Kurve der Polytropen mit  ergibt. Je schneller der Prozess abläuft, desto mehr nähert sich die Kurve der isentropen Zustandsänderung an.
ergibt. Je schneller der Prozess abläuft, desto mehr nähert sich die Kurve der isentropen Zustandsänderung an.
Sonderfälle der polytropen Zustandsänderung
Der Polytropenexponent n kommt dir vielleicht noch von der isentropen Zustandsänderung bekannt vor. Hier kommt der Isentropenexponent  zur Anwendung.
zur Anwendung.
Jede Zustandsänderung ist durch einen eigenen Polytropenexponenten definiert. Für die isobare ist n gleich Null, sodass der Druck konstant bleibt. Bei der isochoren ist n gleich unendlich und das Volumen bleibt konstant. Im Fall der isothermen ist n gleich eins, wodurch die Temperatur konstant bleibt.
Isobare Zustandsänderung:  für n=0
für n=0
Isochore Zustandsänderung:  für n→ꚙ
für n→ꚙ
Isotherme Zustandsänderung:  für n=1
für n=1
Isentrope Zustandsänderung:  für
für 
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Berechnung der Volumenarbeit
Gucken wir uns nun an wie wir die Volumenänderungsarbeit der Zustandsänderungen berechnen können. Für n≠1 gilt:

Wenn der Polytropenexponent gleich Null ist, dann dürfen wir nur die linke Formel verwenden, da sonst im Exponenten durch Null geteilt wird. Für n gleich eins, also für die isotherme Volumenänderungsarbeit gibt es eine weitere Formel:

Schauen wir uns an was für die Volumenarbeit rauskommt, wenn wir die jeweiligen Polytropenexponenten in die Formeln einfügen. Für die isobare Volumenänderungsarbeit ergibt sich:

R ist die universelle Gaskonstante. Für die isotherme Volumenänderungsarbeit (n=1) ergibt sich die bereits erwähnte Formel:
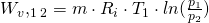 .
.
Im isentropen Fall erhalten wir:

Bei der isochoren Zustandsänderung ändert sich das Volumen nicht und daher wird auch keine Volumenarbeit verrichtet. Das ergibt sich auch wenn wir den entsprechenden Polytropenexponenten in die Formel einfügen:

Jetzt weißt du bestens über die polytrope Zustandsänderung Bescheid. Gucken wir uns nochmal kurz die wichtigsten Punkte an. Für die polytropen Zustandsänderungen gilt, dass  konstant bleibt. Mit dieser Formel können wir jede Zustandsänderung darstellen, indem wir den jeweiligen Polytropenexponenten n einfügen.
konstant bleibt. Mit dieser Formel können wir jede Zustandsänderung darstellen, indem wir den jeweiligen Polytropenexponenten n einfügen.
Druckänderungsarbeit
Die Druckänderungsarbeit (reversible technische Arbeit) können wir im polytropen Fall mit folgender Formel berechnen:

Wir können die Druckänderungsarbeit demnach über die bereits oben erwähnte Formel für die Volumenänderungsarbeit herleiten. Die Druckänderungsarbeit entspricht der Fläche im p-V-Diagramm unter der Polytropen zur p-Achse hin.
Wärme
Um die Wärme bei der polytropen Zustandsänderung zu bestimmen, nehmen wir uns die Formel für die Änderung der inneren Energie zu Hilfe:

Lösen wir die Gleichung nach der Wärme auf erhalten wir:

Für die Volumenänderungsarbeit setzen wir in die Gleichung für die Wärme folgenden Ausdruck ein:

Für die Änderung der inneren Energie wird der Term:

eingesetzt, wodurch wir schließlich für die Wärme Q festhalten können:

-
 = spezifische molare Wärmekapazität
= spezifische molare Wärmekapazität
Durch Zusammenfassen resultiert für die Wärme der Ausdruck:

Bei einem reversiblen Prozess fällt dabei die Dissipationsarbeit weg ( .
.
Ersetzen wir  mit
mit  vereinfacht sich die Formel zu:
vereinfacht sich die Formel zu:
 ; falls
; falls 
Entropie
Bei der polytropen Zustandsänderung können wir die Entropie über drei verschiedene Formeln berechnen:



- cvm = spezifische molare Wärmekapazität bei konstantem Volumen
- cpm = spezifische molare Wärmekapazität bei konstantem Druck
- Ri = spezifische Gaskonstante
Wir können die Entropie darüber hinaus auch im einem T-s-Diagramm darstellen. Allgemein gilt für die Entropie:



