Isotherme Zustandsänderung
In diesem Beitrag widmen wir uns der isothermen Zustandsänderung. Du erfährst wie der Verlauf im p-V- sowie T-s-Diagramm aussieht und wie sich die thermischen Zustandsgrößen verhalten. In unseren anderen Beiträgen erhältst du alle wichtigen Informationen über die isobare , isochore und die adiabatische Zustandsänderung .
Zustandsänderungen von Gasen sind komplexe Prozesse. Zur Vereinfachung können thermodynamische Vorgänge in Teilprozesse zerlegt werden. Hierbei werden eine oder auch mehrere Zustandsgrößen als konstant angenommen. Ein Beispiel für einen komplexen thermodynamischen Vorgang ist der Kreisprozess eines Verbrennungsmotors. Erst durch die Aufgliederung in einzelne Arbeitstakte lässt sich die Funktionsweise mit Hilfe von thermodynamischen Gesetzen erklären.
„Isotherm“ ist griechisch und bedeutet „gleiche Temperatur“. Das bedeutet, dass die Temperatur bei der Zustandsänderung konstant bleibt. T=konst. → T1=T2. Der Druck und das Volumen ändern sich hingegen. Mit der isothermen Expansion und der isothermen Kompression gibt es zwei Möglichkeiten die Temperatur konstant zu halten. Schauen wir uns beide an.
Inhaltsübersicht
Isotherme Expansion und Kompression
Bei der isothermen Expansion wird einem Gas Wärme zugeführt, wodurch es sich ausdehnt und Volumenarbeit verrichtet. Durch die Volumenausdehnung wird die Temperatur konstant gehalten.
Bei der isothermen Kompression wird durch äußere Arbeit das Volumen komprimiert und verdichtet. Dadurch entsteht Wärmeenergie, welche abgeführt werden muss.
Die innere Energie  ändert sich durch Wärmetransport oder Verrichtung von Arbeit. Für die Änderung gilt:
ändert sich durch Wärmetransport oder Verrichtung von Arbeit. Für die Änderung gilt:
 bzw.
bzw. 
Die zweite Gleichung entspricht dem ersten Hauptsatz der Thermodynamik .
- N = Teilchenanzahl
- k = Boltzmann-Konstante
-
 = Temperaturveränderung
= Temperaturveränderung
Da sich die Temperatur aber nicht ändert und demnach  gilt, ändert sich die innere Energie auch nicht. Ebenso ist die Enthalpie H
von der Veränderung der Temperatur abhängig und bleibt demnach bei einer isothermen Zustandsänderung gleich.
gilt, ändert sich die innere Energie auch nicht. Ebenso ist die Enthalpie H
von der Veränderung der Temperatur abhängig und bleibt demnach bei einer isothermen Zustandsänderung gleich.
 und
und  .
.
Wärme
Bei der isothermen Expansion wird dem Gas eine Wärme Q zugeführt, wodurch es sich ausdehnt und die Volumenarbeit -W verrichtet.
 .
.
Bei der isothermen Kompression hingegen wirkt auf das Gas von außen eine Arbeit W. Das Volumen wird kleiner und die dabei entstehende Wärme -Q muss abgeführt werden.
 .
.
Die bei gleicher Temperatur zu verrichtende Arbeit ist bei der Kompression und der Expansion betragsmäßig identisch. Da es sich außerdem um einen reversiblen Prozess handelt, kann die Dissipationsarbeit  vernachlässigt werden.
vernachlässigt werden.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Thermische Zustandsgleichung
Setzen wir die konstant bleibende Temperatur in das ideale Gasgesetz ein, dann folgt daraus:

- n = Stoffmenge [mol]
- R = universelle/molare Gaskonstante [8,3144598
 ]
] - T = Temperatur [K]
-
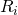 = individuelle/spezifische Gaskonstante
= individuelle/spezifische Gaskonstante - m = Masse [kg]
- p = Druck [Pa]
- V = Volumen [
 ]
]
für 


Anders als bei der isochoren und isobaren Zustandsänderung ist dieser Term nun umgekehrt proportional und als Gesetz von Boyle-Mariotte bekannt. Je nachdem welche Größe wir suchen, können wir dann die Formel umstellen.
p-V- und T-s-Diagramm
Betrachten wir nun das p-V-Diagramm und das T-s-Diagramm. Die Zustandskurve verläuft im p-V-Diagramm wie eine gleichseitige Hyperbel. Diese wird Isotherme genannt.
Der Druck sinkt von Zustand 1 auf 2, wohingegen das Volumen steigt.
Im T-s-Diagramm stellt sich ein paralleler Verlauf zur x-Achse ein, da sich die Temperatur nicht ändert.
Die Fläche unter der Kurve entspricht der Summe aus der Wärme Q und der Dissipationsarbeit. Bei der isothermen Zustandsänderung entspricht diese Fläche auch der Volumenänderungsarbeit und demnach auch der Fläche im p-V-Diagramm. Da die Enthalpie und die Änderung der inneren Energie gleich Null sind, kann bewiesen werden:

Bei einem reversiblen Prozess kann die Dissipationsarbeit vernachlässigt werden und wir erhalten den Zusammenhang zwischen der Wärme und der verrichteten Arbeit.
Berechnung der Volumenarbeit
Die Fläche unter der Isotherme im p-V-Diagramm entspricht der verrichteten Arbeit W und lässt sich bei Annahme eines idealen Gases mit Hilfe der folgenden Formel berechnen:

Lösen wir die thermische Zustandsgleichung nach p auf

und setzen p in die Gleichung der Volumenänderungsarbeit ein, erhalten wir:

Da sowohl T, als auch m und 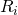 konstant sind ergibt sich:
konstant sind ergibt sich:


Setzen wir für  stattdessen
stattdessen  ein, erhalten wir schließlich:
ein, erhalten wir schließlich:

Druckänderungsarbeit
Die Druckänderungsarbeit entspricht bei der isothermen Zustandsänderung der Volumenänderungsarbeit. Die Gleichungen können wir durch das Gesetz von Boyle-Mariotte ineinander überführen.

Entropie
Die in einem System vorhandene Entropie ist von der Aufnahme bzw. Abgabe von Wärme abhängig. Die Änderung der Entropie sieht folgendermaßen aus:
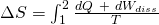
Wie wir bereits wissen gilt  und
und  .
.
Daraus folgt für die Formel der Entropieänderung:

Durch Umformen mit Hilfe der thermischen Zustandsgleichung erhalten wir das Entropiedelta in Abhängigkeit zur Volumenveränderung:

Wollen wir die Entropieänderung über den Druck beschreiben, müssen wir das Gesetz von Boyle-Mariotte anwenden:

Die Entropie lässt sich in einem T-s-Diagramm darstellen. Es gilt:

Fassen wir kurz zusammen, was wir gelernt haben. Bei der isothermen Zustandsänderung bleibt die Temperatur konstant. Die Zustandskurve im p-V-Diagramm entspricht einer Hyperbel und im T-s-Diagramm ist sie eine Konstante. In Summe ist die Änderung der inneren Energie gleich null.



