Otto Prozess
Wenn du vom Otto Prozess hörst, dann denkst du bestimmt direkt an den Otto-Motor. In diesem Beitrag erklären wir dir, wie die thermodynamischen Zusammenhänge in diesem aussehen, indem wir die Abläufe mittels p-V- und T-S- Diagramm des Otto Kreisprozesses betrachten. Zum Schluss zeigen wir dir, wie man den Otto Prozess berechnen kann.
Inhaltsübersicht
Vorgehen beim Otto Prozess
Bei der Betrachtung des Otto-Motors tätigen wir ein paar Vereinfachungen. Daher handelt es sich beim Otto Prozess nicht um den genauen thermodynamischen Ablauf, sondern um einen Vergleichsprozess. Die Idealisierung erfolgt, indem wir annehmen, dass es keine Reibung gibt und die Kompression sowie Expansion adiabat ablaufen. Das bedeutet, dass es keinen Wärme- und Stoffaustausch mit der Umgebung gibt. Des Weiteren gehen wir von einem idealen Gas als Arbeitsfluid aus.
Bevor wir uns den thermischen Zustandsänderungen zuwenden, solltest du dich vergewissern, dass du die vier Arbeitstakte Ansaugen, Verdichten, Arbeiten und Ausstoßen eines Otto-Motors noch kennst, wenn nicht, solltest du dir zuerst unser Video dazu noch einmal ansehen.
Otto Prozess im p-V- und T-S-Diagramm
Zur Untersuchung der Abläufe betrachten wir das p-V- und das T-S-Diagramm vom Ottomotor Kreisprozess.
Die 4 Prozessschritte bzw. Takte beim Otto Prozess sind:
- Isentrope Kompression
- Isochore Wärmezufuhr
- Isentrope Expansion
- Isochore Wärmeabfuhr bzw. Ladungswechsel
Im Folgenden schauen wir uns den Ablauf der Takte genauer an:
Isentrope Kompression 1 -> 2:
Im ersten Schritt wird das Gas isentrop komprimiert bzw. durch den aufsteigenden Kolben verdichtet. Dafür wird dem System Arbeit zugeführt .
Infolge dessen steigt der Druck und das Volumen sinkt. Da bei einer isentropen Zustandsänderung keine Wärme zu- oder abgeführt wird, bleibt die Entropie konstant, während die Temperatur steigt.
Isochore Wärmezufuhr 2 -> 3:
Als nächstes folgt eine isochore Wärmezufuhr  durch die Verbrennung des Gasgemisches. Da dieser Prozess sehr schnell abläuft, ändert sich das Volumen nicht. Nur der Druck steigt. Man spricht daher auch von einem „Gleichraum-Prozess“. Durch die Wärmezufuhr steigen die Temperatur und die Entropie im System.
durch die Verbrennung des Gasgemisches. Da dieser Prozess sehr schnell abläuft, ändert sich das Volumen nicht. Nur der Druck steigt. Man spricht daher auch von einem „Gleichraum-Prozess“. Durch die Wärmezufuhr steigen die Temperatur und die Entropie im System.
Isentrope Expansion 3 -> 4:
Nun folgt wieder eine isentrope Expansion, bei der der Kolben nicht mehr fixiert wird. Bei diesem Vorgang verrichtet das Gas Arbeit, wodurch sich das Volumen vergrößert und der Druck im System sinkt. Auch hier liegt wieder kein Wärmeaustausch vor. Die Entropie bleibt also konstant und die Temperatur sinkt.
Isochore Wärmeabfuhr bzw. Ladungswechsel 4 -> 1:
Der letzte Schritt wird auch als isochorer Ladungswechsel bezeichnet. Hier werden die Abgase aus dem Kolben gestoßen und frische Luft angesaugt. Dabei fällt der Druck wieder auf den Druck des Anfangszustands. Der Ausstoß des heißen Abgases sorgt für eine Wärmeabfuhr der Wärme  aus dem System. Folglich fallen auch die Temperatur und die Entropie.
aus dem System. Folglich fallen auch die Temperatur und die Entropie.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Weitere Vergleichsprozesse
Berechnung des Otto-Kreisprozesses
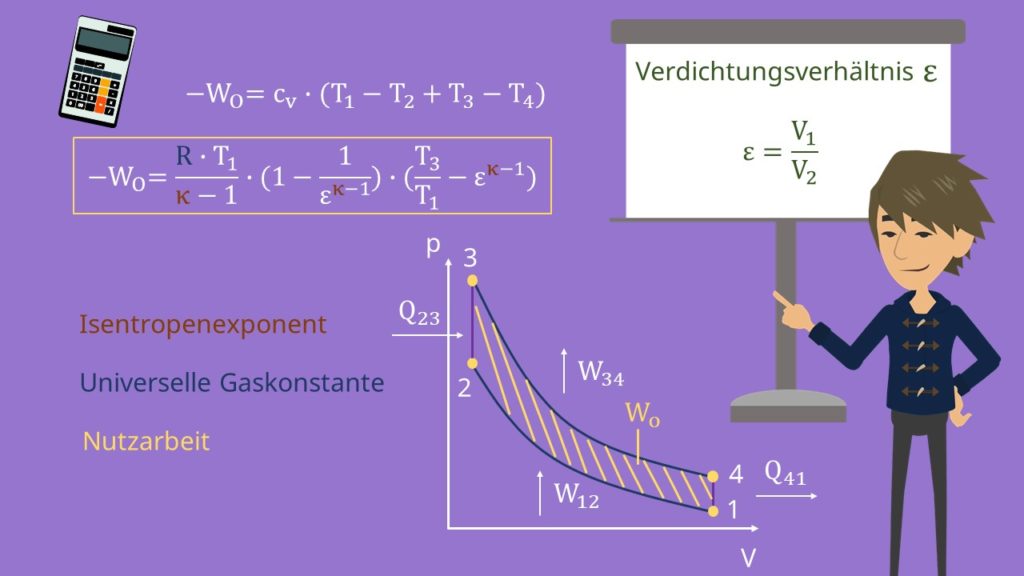
Jetzt wissen wir, wie die thermodynamischen Prozesse ablaufen. Untersuchen wir als nächstes, wie wir den Otto-Kreisprozess berechnen können, angefangen mit der Nutzarbeit. Diese setzt sich zusammen aus der zugeführten und abgeführten Wärme:

Sind uns die Temperaturen und die isochore spezifische Wärmekapazität bekannt, dann gilt:

Ein charakteristischer Parameter für Verbrennungsmotoren ist das Verdichtungsverhältnis ε. Dabei handelt es sich um das Verhältnis zwischen dem Volumen vor und nach der Verdichtung  . Daraus folgt für uns:
. Daraus folgt für uns:
Kappa ist der Isentropenexponent und R die universelle Gaskonstante. Die Nutzarbeit wird auch durch die Fläche, welche durch die Kurven im p-V-Diagramm eingeschlossen wird, dargestellt.
Otto Prozess: Thermischer Wirkungsgrad
Betrachten wir jetzt den Wirkungsgrad des Otto Prozesses. Dieser entspricht dem Betrag der Nutzarbeit geteilt durch die zugeführte Wärme:

Verwenden wir wieder das Verdichtungsverhältnis ε, dann können wir den Wirkungsgrad folgendermaßen berechnen:

Das zeigt uns, dass der Wirkungsgrad unabhängig von der Maximaltemperatur des Systems ist und nur vom Verdichtungsverhältnis und dem Isentropenexponenten abhängt. Allerdings können wir das Verdichtungsverhältnis nicht beliebig steigern, weil sich mit der wachsenden Verdichtung auch die Verdichtungstemperatur T2 erhöht. Überschreiten wir dabei die Selbstzündtemperatur, dann kommt es zu einer unkontrollierten Verbrennung im Motor. Man spricht auch vom „Klopfen“ bzw. einer „klopfenden“ Verbrennung. Dabei können Schäden entstehen. In modernen Ottomotoren liegt das Verdichtungsverhältnis bei circa 10 (ε≈10).
Fassen wir nochmal kurz zusammen. Der Otto Prozess ist ein idealisierter Vergleichsprozess für den Otto-Motor. Es liegen jeweils zwei isentrope und zwei isochore Zustandsänderungen vor. Der Wirkungsgrad ist abhängig vom Verdichtungsverhältnis im System und wird durch die Selbstzündtemperatur begrenzt.