Entropie-Übung / Entropieänderung
Du hattest sicher schon einmal einen Platten am Fahrrad und musstest deshalb eine Luftpumpe verwenden. Was diese mit der Entropieänderung zu tun hat und wie du die entsprechende Entropieänderung berechnen kannst, erfährst du im Folgenden.
Inhaltsübersicht
Wie lässt sich eine Entropieänderung berechnen?
Du kennst sicherlich bereits die allgemeine Entropiebilanz:
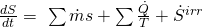
Diese Entropiebilanz trifft auch auf eine Fahrradpumpe zu, die zu den Verdichtern oder Kompressoren zählt, was einen wichtigen Aspekt für die Entropieänderung darstellt.
Ein Verdichter stellt einen irreversiblen Zustand dar. Dies erkennst du an dem  . Er hat prinzipiell die Aufgabe den Druck zu erhöhen, indem er dem System technische Leistung zuführt. Du weißt ja, dass ein Elektromotor dann gerne einmal heiß wird. Deshalb wird der Verdichter mit Hilfe von Umgebungsluft gekühlt.
. Er hat prinzipiell die Aufgabe den Druck zu erhöhen, indem er dem System technische Leistung zuführt. Du weißt ja, dass ein Elektromotor dann gerne einmal heiß wird. Deshalb wird der Verdichter mit Hilfe von Umgebungsluft gekühlt.
Entropieänderung anhand eines Verdichters erklärt
Wir betrachten zur Erklärung der Entropieänderung jetzt einen Verdichter, den Luft mit einem Massenstrom von 0,5 Kilogramm pro Sekunde durchfließt. Die Luft hat dabei zu Beginn die Temperatur  gleich 320 Kelvin und einen Druck
gleich 320 Kelvin und einen Druck  von 0,1 Megapascal. Der Verdichter arbeitet isotherm, also ohne Temperaturänderung. Er verdichtet auf einen Druck
von 0,1 Megapascal. Der Verdichter arbeitet isotherm, also ohne Temperaturänderung. Er verdichtet auf einen Druck  von 0,7 Megapascal, wobei er dafür eine Leistung
von 0,7 Megapascal, wobei er dafür eine Leistung  von 100 Kilowatt benötigt. Die Umgebungsluft hat eine Temperatur von 298,15 Kelvin. Die Molmasse von Luft beträgt 28,949 Gramm pro Mol.
von 100 Kilowatt benötigt. Die Umgebungsluft hat eine Temperatur von 298,15 Kelvin. Die Molmasse von Luft beträgt 28,949 Gramm pro Mol.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Entropieänderung bei Reibung und Wärmeübergang
Um die Entropieänderung berechnen zu können, wollen wir jetzt herausfinden, wie viel Entropie durch Reibung und den Wärmeübergang produziert wird. Dafür machen wir eine Entropiebilanz um den gesamten Verdichter. Das heißt, wir haben ein- und austretende Massenströme sowie einen Wärmestrom nach außen und natürlich die irreversible Entropieproduktion.

Da wir den Verdichter mit einem konstanten Massenstrom durchfließen und der Wärmestrom auch als konstant angesehen werden kann, können wir einen stationären Fließprozess annehmen. Dadurch wird 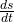 zu null. Weiterhin ist der Massenstrom beim Eintreten natürlich derselbe wie beim Austritt:
zu null. Weiterhin ist der Massenstrom beim Eintreten natürlich derselbe wie beim Austritt:
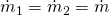
Damit können wir die Entropiebilanz zusammenfassen zu:

und anschließend nach  umstellen:
umstellen:

Entropieänderung durch Verdichter
Jetzt müssen wir also nur noch die Entropie vor und nach dem Verdichter sowie den Wärmestrom bestimmen und kennen dann die Entropieproduktion.
Die Entropieänderung berechnen können wir mit:

Nun verdichten wir isotherm. Das heißt:  ist gleich
ist gleich  . Damit wird der Bruch zu eins. Zudem weißt du bestimmt, dass der
. Damit wird der Bruch zu eins. Zudem weißt du bestimmt, dass der  immer null ist. Wir können ihn also streichen.
immer null ist. Wir können ihn also streichen.
Jetzt fehlt nur noch der Wärmestrom. Den erhalten wir aus einer Energiebilanz um das System.

Zur Berechnung der Entropieänderung benötigen wir die Änderung der Energie, welche wieder null ist, da wir davon ausgehen können, dass der Prozess stationär abläuft. Die Enthalpie-Differenz erhalten wir aus der kalorischen Zustandsgleichung:
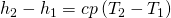
Da wir isotherm verdichten, ist die Enthalpie-Differenz gleich null. Wir erhalten für den Wärmestrom:

Setzen wir das in unsere Entropiebilanz ein, erhalten wir:

Jetzt haben wir aber zwei Temperaturen und wissen nicht genau, welche wir verwenden sollen. Dafür gibt es eine ganz einfache Regel: Wir nehmen immer die Temperatur, bei der unser Wärmestrom über die Grenze tritt. Wir haben die Grenze um den ganzen Verdichter gelegt. Das heißt, der Wärmestrom tritt über die Grenze, wenn er außerhalb des Verdichters ist. Damit ist die Temperatur, mit der der Wärmestrom über die Grenze tritt, genau unsere Umgebungstemperatur  . So erhalten wir für
. So erhalten wir für  :
:

Die irreversible Entropieproduktion ist größer null und verstößt somit nicht gegen den zweiten Hauptsatz der Thermodynamik. Allerdings sorgt das dafür, dass der Verdichter nicht reversibel betrieben werden kann.
Endlich bist du bestens darüber informiert, wie man die Entropieänderung berechnen kann und bei der nächsten Fahrradtour kannst du deinen Freunden gleich erklären, was die Luftpumpe mit der Entropieänderung zu tun hat.





