Beschränktes Wachstum
In diesem Artikel erklären wir dir beschränktes Wachstum beziehungsweise begrenztes Wachstum ausführlich anhand von Beispielen. Am Ende findest du auch Aufgaben mit Lösungen zu diesem Thema.
Wenn du das Thema beschränktes Wachstum in kürzester Zeit erlernen möchtest, dann ist unser Video genau das Richtige für dich.
Inhaltsübersicht
Beschränktes Wachstum einfach erklärt
Wie bei allen Wachstumsprozessen, so betrachtest du auch für beschränktes Wachstum (oder begrenztes Wachstum genannt) die zeitliche Entwicklung einer sogenannten Population. Der Begriff Population ist sehr allgemein. Du könntest dir darunter beispielsweise die Anzahl an verkauften Cola-Dosen in deiner Region oder die Spannung an einem Kondensator vorstellen.
Beschränktes Wachstum besitzt eine Besonderheit, nämlich die Existenz einer natürlichen Schranke. Diese Schranke kann die Population nach oben oder nach unten beschränken. Das heißt, dass die Population die Schranke niemals überschreiten (bei nach oben beschränktem Wachstum) beziehungsweise unterschreiten kann (bei nach unten beschränktem Wachstum).
Wie es typisch für Wachstumsprozesse ist, gibt es auch für beschränktes Wachstum eine zugrunde liegende Differentialgleichung
Beschränktes Wachstum oder begrenztes Wachstum ist durch die folgende lineare inhomogene Differentialgleichung gegeben
 .
.
Dabei bedeuten die Parameter folgendes:
-
 : Population in Abhängigkeit von der Zeit
: Population in Abhängigkeit von der Zeit  ,
, -
 : Wachstumskonstante und
: Wachstumskonstante und -
 : Wert der Schranke.
: Wert der Schranke.
Die Differenz  wird auch als Sättigungsmanko oder Restbestand bezeichnet.
wird auch als Sättigungsmanko oder Restbestand bezeichnet.
Beschränktes Wachstum Formel
Die Differentialgleichung für beschränktes Wachstum lässt sich mit Hilfe der Variablentrennung lösen. Wir geben in diesem Abschnitt nur die Lösung wieder und veranschaulichen diese anhand eines konkreten Beispiels. Wir werden auch eine graphische Herleitung der Lösungsformel für beschränktes Wachstum vorstellen.
Beginnen wir mit der Lösungsformel:
Die Lösung der Differentialgleichung liefert folgende Wachstumsfunktion für beschränktes Wachstum (begrenztes Wachstum)
 .
.
Die Zahl 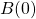 stellt die Population zum Zeitpunkt
stellt die Population zum Zeitpunkt  dar. Lass dich an dieser Stelle nicht davon irritieren, dass in der Lösungsformel subtrahiert wird, obwohl wir von einem Wachstum sprechen. Hier ist das Vorzeichen des Sättigungsmankos entscheidend.
dar. Lass dich an dieser Stelle nicht davon irritieren, dass in der Lösungsformel subtrahiert wird, obwohl wir von einem Wachstum sprechen. Hier ist das Vorzeichen des Sättigungsmankos entscheidend.
Für nach oben beschränktes Wachstum stellt die Schranke  eine obere Grenze dar. Es gilt also
eine obere Grenze dar. Es gilt also  . Damit ist die Differenz
. Damit ist die Differenz  positiv. Die Exponentialfunktion
positiv. Die Exponentialfunktion
 ist für alle Werte von
ist für alle Werte von  positiv. Somit ist auch das Produkt
positiv. Somit ist auch das Produkt 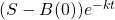 positiv. Es wird also von
positiv. Es wird also von  eine positive Zahl abgezogen, die aber mit steigendem
eine positive Zahl abgezogen, die aber mit steigendem  immer kleiner wird. Folglich wird
immer kleiner wird. Folglich wird  immer größer – wir haben daher das gewünschte Wachstum.
immer größer – wir haben daher das gewünschte Wachstum.
Beachte, dass das Produkt 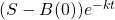 zwar immer kleiner wird, aber nur für den Grenzfall
zwar immer kleiner wird, aber nur für den Grenzfall  gleich Null ist. Somit ist
gleich Null ist. Somit ist  immer kleiner als
immer kleiner als  und nur im Grenzfall gleich
und nur im Grenzfall gleich  . Das ist gerade die Beschränktheit des Wachstums, die gewünscht war.
. Das ist gerade die Beschränktheit des Wachstums, die gewünscht war.
Vorsicht: Die umgekehrte Situation, also das  gilt, heißt beschränkter Zerfall oder beschränkte Abnahme. Diesen Fall behandeln wir in einem eigenen Abschnitt weiter unten.
gilt, heißt beschränkter Zerfall oder beschränkte Abnahme. Diesen Fall behandeln wir in einem eigenen Abschnitt weiter unten.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Beispiel
Lass uns der abstrakten Lösungsformel eine anschauliche Gestalt in Form eines konkreten Funktionsgraphen
geben. Hierzu wählen wir die Parameter der Lösungsformel für beschränktes Wachstum folgendermaßen:  ,
,  und
und  . Setzen wir diese Werte in die allgemeine Formel ein, erhalten wir
. Setzen wir diese Werte in die allgemeine Formel ein, erhalten wir
 .
.
Wenn wir diese Funktion in ein Koordinatensystem einzeichnen, bekommen wir den folgenden Funktionsgraphen.
Diese Funktion könnte beispielsweise die Anzahl an zugestellten Zeitschriften in einer Gegend von 100 Haushalten modellieren. Das  ist, spiegelt in diesem Fall die Tatsache wider, dass zu Beginn noch keine Zeitschriften zugestellt wurden. Du kannst an diesem Bild die Wirkung der Schranke
ist, spiegelt in diesem Fall die Tatsache wider, dass zu Beginn noch keine Zeitschriften zugestellt wurden. Du kannst an diesem Bild die Wirkung der Schranke  erkennen. Je größer
erkennen. Je größer  wird, umso näher befinden sich die Funktionswerte an der Schranke
wird, umso näher befinden sich die Funktionswerte an der Schranke  . Sie werden aber niemals größer. Das macht im Fall der zugestellten Zeitschriften auch Sinn, denn der Zusteller liefert den 100 Haushalten auch nur 100 Exemplare einer gegebenen Zeitschrift. Wir haben hier also einen klassischen Fall für ein nach oben beschränktes Wachstum.
. Sie werden aber niemals größer. Das macht im Fall der zugestellten Zeitschriften auch Sinn, denn der Zusteller liefert den 100 Haushalten auch nur 100 Exemplare einer gegebenen Zeitschrift. Wir haben hier also einen klassischen Fall für ein nach oben beschränktes Wachstum.
Herleitung anhand eines einfachen Beispiels
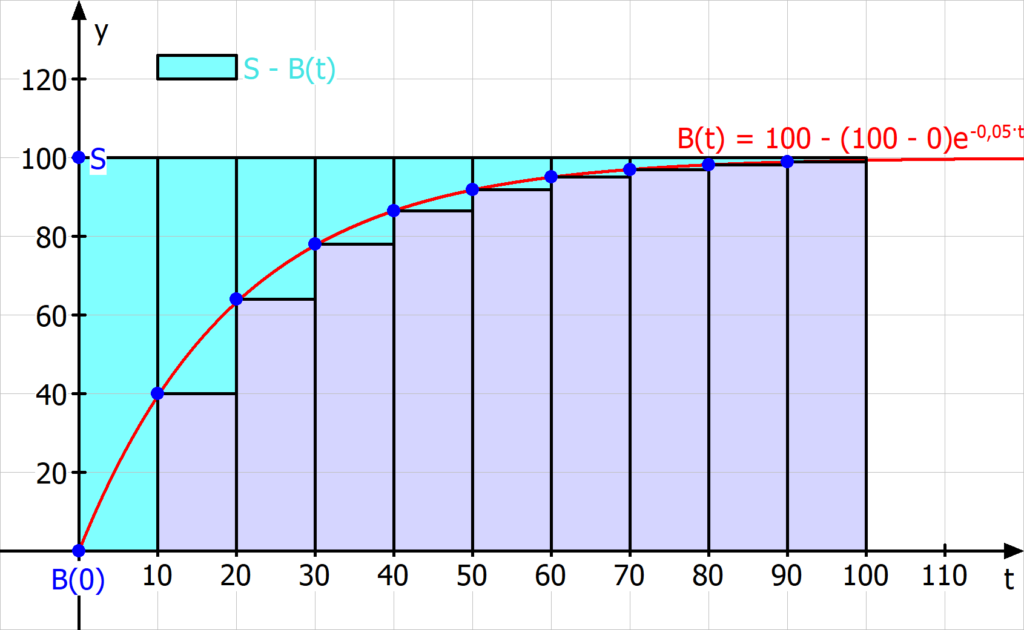
Nehmen wir uns nochmal das Beispiel von vorhin her und zeichnen im Intervall [0, 100] für jeden zehnten Wert das Sättigungsmanko ein. Dazu teilen wir das Intervall in zehn Abschnitte, die jeweils die Breite 10 besitzen. Für den Wert der Population  in der Differenz
in der Differenz  nehmen wir immer den Anfang jedes Teilintervalls. Das folgende Bild soll diesen Prozess illustrieren.
nehmen wir immer den Anfang jedes Teilintervalls. Das folgende Bild soll diesen Prozess illustrieren.
Die blauen Punkte entsprechen genau den Werten am Anfang jedes Teilintervalls. Die türkis gefärbte Fläche entspricht der Differenz  , also dem Sättigungsmanko. Wenn wir uns nur auf das Sättigungsmanko konzentrieren und die zehn Werte in ein eigenes Koordinatensystem einzeichnen, erhalten wir die folgende Grafik.
, also dem Sättigungsmanko. Wenn wir uns nur auf das Sättigungsmanko konzentrieren und die zehn Werte in ein eigenes Koordinatensystem einzeichnen, erhalten wir die folgende Grafik.
An der Grafik können wir erkennen, dass der Verlauf des Sättigungsmankos dem einer exponentiellen Abnahme gleicht. Wir können also festhalten, dass folgende Gleichung für das Sättigungsmanko gilt
Sättigungsmanko:  .
.
Hier ist  eine Konstante, die zu bestimmen ist und
eine Konstante, die zu bestimmen ist und  die Wachstumskonstante. Der Wert von
die Wachstumskonstante. Der Wert von  gibt den Wert des Sättigungsmankos zum Zeitpunkt
gibt den Wert des Sättigungsmankos zum Zeitpunkt  an. Für das konkrete Beispiel ist
an. Für das konkrete Beispiel ist  und
und  . Somit gilt
. Somit gilt

 .
.
Zum Zeitpunkt  ist
ist  , also folgt das
, also folgt das  ist. Wir erhalten daher
ist. Wir erhalten daher
 ,
,
was gerade die Funktionvorschrift unseres Beispiels war.
Im Allgemeinen muss nicht  gelten. Dann ist
gelten. Dann ist  und wir bekommen
und wir bekommen
 .
.
Diese Gleichung ist gerade die allgemeine Lösungsformel für beschränktes Wachstum.
Beschränkter Zerfall / Beschränkte Abnahme
Bisher haben wir uns nur den Fall  angesehen, der beschränktes Wachstum beziehungsweise begrenztes Wachstum darstellt. Für
angesehen, der beschränktes Wachstum beziehungsweise begrenztes Wachstum darstellt. Für  erhalten wir den Fall des sogenannten beschränkten Zerfalls oder der beschränkten Abnahme. Die Lösungsformel dafür ist
erhalten wir den Fall des sogenannten beschränkten Zerfalls oder der beschränkten Abnahme. Die Lösungsformel dafür ist
 .
.
Sie sieht genauso aus wie für das begrenzte Wachstum. Wo liegt also der Unterschied? Der Unterschied liegt im Vorzeichen des Sättigungsmankos  zum Zeitpunkt
zum Zeitpunkt  . Für begrenztes Wachstum war dieses positiv und wir hatten gesehen, dass die Population dann tatsächlich mit der Zeit wächst. Für den beschränkten Zerfall ist das Vorzeichen negativ. Die genau gleiche Argumentation wie für begrenztes Wachstum führt zum Schluss, dass die Population
. Für begrenztes Wachstum war dieses positiv und wir hatten gesehen, dass die Population dann tatsächlich mit der Zeit wächst. Für den beschränkten Zerfall ist das Vorzeichen negativ. Die genau gleiche Argumentation wie für begrenztes Wachstum führt zum Schluss, dass die Population  abnimmt. Für fortschreitende Zeit
abnimmt. Für fortschreitende Zeit  , werden die Funktionswerte
, werden die Funktionswerte  immer kleiner, unterschreiten jedoch nicht die Schranke
immer kleiner, unterschreiten jedoch nicht die Schranke  . In diesem Zusammenhang spricht man davon, dass
. In diesem Zusammenhang spricht man davon, dass  die Population nach unten beschränkt.
die Population nach unten beschränkt.
Wenn wir unser oberes begrenztes Wachstum Beispiel nehmen und den Anfangswert 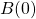 auf 200 statt 0 setzen, erhalten wir folgenden Funktionsgraphen.
auf 200 statt 0 setzen, erhalten wir folgenden Funktionsgraphen.
Da die Differenz  negativ ist, findest du manchmal für den beschränkten Zerfall auch die Darstellung
negativ ist, findest du manchmal für den beschränkten Zerfall auch die Darstellung

Wie beim beschränkten Wachstum solltest du dich nicht davon irritieren lassen, dass hier zwei Zahlen  und
und  miteinander addiert werden, obwohl wir hier einen Zerfall beziehungsweise eine Abnahme vorliegen haben. Die Zahl
miteinander addiert werden, obwohl wir hier einen Zerfall beziehungsweise eine Abnahme vorliegen haben. Die Zahl  , die zu
, die zu  addiert wird, wird aufgrund der Exponentialfunktion immer kleiner. Damit wird auch die Addition
addiert wird, wird aufgrund der Exponentialfunktion immer kleiner. Damit wird auch die Addition  immer kleiner – also nimmt die Population
immer kleiner – also nimmt die Population  tatsächlich ab.
tatsächlich ab.
Beschränktes Wachstum Aufgaben
In diesem Abschnitt stellen wir dir zwei Aufgaben vor. Bei der ersten geht es um das Bestimmen aller Parameter der Lösungsformel und um den Umgang mit der Lösungsformel beim Berechnen bestimmter Zeitpunkte. Bei der zweiten Aufgabe hingegen ist die Funktion gegeben und es sind aus ihr die Parameter zu extrahieren.
Aufgabe 1: Parameter für beschränktes Wachstum bestimmen
In einer Stadt mit 10.000 Einwohnern hat der Hersteller der brandneuen Spielekonsole „GAM G Pro“ einen neuen Standort eröffnet. Mit 20% Rabatt für eine Konsole pro Haushalt, versucht der Hersteller seine Konsole zu verkaufen. Die Werbung funktioniert und bereits nach 3 Tagen wurden 4.000 Exemplare verkauft.
(a) Die Anzahl an verkauften „GAM G Pro“-Konsolen soll als beschränktes Wachstum modelliert werden. Bestimme hierzu die Parameter  ,
, 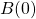 und
und  und schreibe die Lösungsformel mit allen Parameterwerten hin.
und schreibe die Lösungsformel mit allen Parameterwerten hin.
(b) Der Hersteller der Konsole interessiert sich dafür, wann 90% der Haushalte eine Konsole besitzen. Bestimme den dazugehörigen Zeitpunkt  .
.
Lösung Aufgabe 1
(a) Da jeder Haushalt nur eine Konsole verkauft bekommt, kann die Anzahl an verkauften Konsolen nicht 10.000 übersteigen. Damit ist die Schranke  . Zu Beginn wurden noch keine Konsolen verkauft. Somit ist
. Zu Beginn wurden noch keine Konsolen verkauft. Somit ist  . Zum Bestimmen der Wachstumskonstante
. Zum Bestimmen der Wachstumskonstante  nutzen wir die Information, dass nach drei Tagen 4.000 Konsolen verkauft wurden. Es gilt
nutzen wir die Information, dass nach drei Tagen 4.000 Konsolen verkauft wurden. Es gilt

 .
.
Wir haben somit alle Parameter berechnet und die Funktionsvorschrift lautet


(b) 90% der Haushalte, an denen Konsolen verkauft wurden, entspricht 9.000 verkauften Konsolen. Um den Zeitpunkt  zu bestimmen, setzen wir die bekannten Informationen ein und erhalten
zu bestimmen, setzen wir die bekannten Informationen ein und erhalten
 .
.
Stellen wir diese Gleichung nach  um, bekommen wir
um, bekommen wir
 .
.
Das heißt, nach etwa 14 Tagen wird der Hersteller an 90% der Haushalte seine Konsole verkauft haben.
Aufgabe 2: Ablesen von Parameter und Wachstumsgeschwindigkeit
Die folgende Lösungsformel

soll begrenztes Wachstum modellieren.
(a) Bestimme aus der gegebenen Lösungsformel die Parameter  ,
, 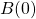 und
und  .
.
(b) Bestimme den Zeitpunkt  zu dem die Wachstumsgeschwindigkeit genau 3 beträgt.
zu dem die Wachstumsgeschwindigkeit genau 3 beträgt.
Lösung Aufgabe 2
(a) Für  nähern sich die Funktionswerte
nähern sich die Funktionswerte  dem Wert 300. Damit ist
dem Wert 300. Damit ist  . Die Wachstumskonstante ist gerade der Faktor vor der Zeit
. Die Wachstumskonstante ist gerade der Faktor vor der Zeit  innerhalb des Arguments der Exponentialfunktion. Somit ist
innerhalb des Arguments der Exponentialfunktion. Somit ist  . Der Faktor vor der Exponentialfunktion entspricht
. Der Faktor vor der Exponentialfunktion entspricht  und folglich gilt
und folglich gilt

oder nach 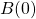 umgestellt
umgestellt
 .
.
(b) Um die Wachstumsgeschwindigkeit zu bestimmen, berechnen wir die erste Ableitung der gegebenen Funktion
 .
.
Wir erhalten
 .
.
Zum Zeitpunkt  gilt
gilt

und umgestellt nach 
 .
.
Logistisches Wachstum
Genauso wie das beschränkte Wachstum, hat auch das Logistische Wachstum eine natürliche Schranke. Beim Logistischen Wachstum wird das Wachstum durch den Verbrauch einer bestimmten Ressource immer kleiner, bis es schließlich zum Stillstand kommt. Damit du über die Wachstumsprozesse in deiner Prüfung genau Bescheid weißt, solltest du dir unbedingt unser Video dazu anschauen. Leg direkt los!