Exponentielles Wachstum
In diesem Beitrag erfährst du, was exponentielles Wachstum ist und welche wichtigen Formeln es dazu gibt. Zusätzlich wirst du viele Beispiele und Aufgaben finden.
Du möchtest das Thema kompakt erklärt bekommen? Dann schau unser Video dazu an!
Inhaltsübersicht
Exponentielles Wachstum einfach erklärt
Exponentielles Wachstum beschreibt, wie alle anderen Wachstumsprozesse auch, die Entwicklung einer Population mit der Zeit. Unter der Population kannst du dir zum Beispiel die Anzahl an Bakterien oder die Dicke eines Papiers vorstellen.
Die definierende Eigenschaft für exponentielles Wachstum ist folgende:
Unterscheiden sich die Werte der Population zwischen zwei benachbarten Zeitpunkten immer um den gleichen Faktor, dann liegt exponentielles Wachstum vor. Insbesondere ist exponentielles Wachstum nicht beschränkt. Die Population kann demnach beliebig große oder beliebig kleine Werte annehmen.
In der Realität sind aber viele Prozesse beschränkt. Wachstumsmodelle, die eine solche Beschränktheit berücksichtigen, sind das beschränkte Wachstum und das logistische Wachstum .
Einfaches Beispiel
Lass uns zu Beginn ein einfaches Beispiel anschauen. Nimm ein Blatt Papier zur Hand und falte es einmal zur Hälfte. Wie dick wird das Papier nach dem ersten Falten sein? Es wird zweimal so dick sein wie das Papier am Anfang. Nun faltest du das Papier ein zweites Mal in der Mitte. Wie dick ist es jetzt? Wieder ist es doppelt so dick wie vor dem zweiten Falten, denn beim Falten hast du zwei Schichten des Papiers über die anderen zwei Schichten gelegt. Im Vergleich zum Papier am Anfang, ist das zweimal gefaltete Papier jetzt viermal so dick.
Erkennst du hier ein Muster? Nach jedem Falten verdoppelt sich die Dicke. Die Dicke des Papiers beim Falten ist also ein klassisches Beispiel für exponentielles Wachstum. Bezeichnen wir die Dicke des Papiers am Anfang willkürlich mit 1, so könnte eine Tabelle mit den Werten für die Dicke nach jedem Falten folgendermaßen aussehen
| Anzahl Faltungen | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Dicke | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
Um von einem Wert der Dicke zum benachbarten Wert zu kommen, multiplizieren wir die Startdicke mit dem Faktor 2 und erhalten die Enddicke. Wenn du also zum Bespiel von der Dicke nach 3 Faltungen zur Dicke nach 4 Faltungen kommen möchtest, dann rechnest du
2 mal Dicke bei 3 Faltungen =  = Dicke bei 4 Faltungen.
= Dicke bei 4 Faltungen.
Du merkst also, dass die Dicke des Papiers ziemlich schnell wächst und zwar immer um denselben Faktor von einer Faltung zur nächsten.
Fun Fact: Ein typisches Blatt Papier ist in etwa 0,1 mm dick. Bereits nach nur 30 Faltungen würde das Papier in den Weltraum reichen. Nach 42 Faltungen erreicht das Papier den Mond.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Exponentielles Wachstum Darstellungsformen
Exponentielles Wachstum kann aber nicht nur die Papierdicke darstellen. Weitere Beispiele, die wir im Verlauf des Beitrags ausführlicher behandeln werden, sind der Zinseszins und die Anzahl an Bakterien. In diesem Abschnitt stellen wir dir zwei Formeln für exponentielles Wachstum vor. Dabei zeigen wir dir, wie du von der einen Formel zur anderen übergehen kannst und wie die rekursive Darstellung des exponentiellen Wachstums aussieht.
Exponentialfunktion und Wachstumsfaktor
Der Name „exponentielles Wachstum“ könnte dir vielleicht schon einen ersten Hinweis darauf geben, wie die Gleichung dafür aussehen wird. Exponentielles Wachstum wird durch sogenannte Exponentialfunktion modelliert. Eine Exponentialfunktion sieht allgemein so aus
 .
.
Dabei ist  der Anfangsbestand zum Zeitpunkt
der Anfangsbestand zum Zeitpunkt  und
und  der Wachstumsfaktor
. Die Bezeichnung „Exponentialfunktion“ kommt daher zustande, dass die Variable
der Wachstumsfaktor
. Die Bezeichnung „Exponentialfunktion“ kommt daher zustande, dass die Variable  im Exponenten steht.
im Exponenten steht.
Explizite Darstellung
Bei Wachstumsprozessen interessierst du dich, wie sich eine Population mit der Zeit ändert. Der Begriff Population ist sehr allgemein. Du könntest dir zum Beispiel die Anzahl an Bakterien, die Menge an Geld auf deinem Bankkonto oder die Papierdicke vorstellen. Für die Zeit wird der Buchstabe  einheitlich verwendet. Für die Population findest du oft die Abkürzung
einheitlich verwendet. Für die Population findest du oft die Abkürzung  . Daher triffst du für exponentielles Wachstum auf die Formel
. Daher triffst du für exponentielles Wachstum auf die Formel

Hier ist
-
 der Anfangsbestand, das heißt, wie viel es von der Population zum Zeitpunkt
der Anfangsbestand, das heißt, wie viel es von der Population zum Zeitpunkt  gibt und
gibt und -
 der Wachstumsfaktor.
der Wachstumsfaktor.
Wenn wir statt  die Zahl
die Zahl  verwenden, erhalten wir eine andere Formel für exponentielles Wachstum
verwenden, erhalten wir eine andere Formel für exponentielles Wachstum

Hier ist 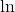 der natürliche Logarithmus
und
der natürliche Logarithmus
und  die Eulersche Zahl.
die Eulersche Zahl.
Manchmal wird mit „Exponentialfunktion“ eine Funktion der Form
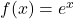
bezeichnet. Korrekterweise sollte das aber Exponentialfunktion zur Basis  heißen. Welche Formel du letztendlich verwendest, ist dir überlassen. Die zweite Darstellung mit der Eulerschen Zahl findest du aber häufig im Zusammenhang mit Differentialgleichungen
in der Physik.
heißen. Welche Formel du letztendlich verwendest, ist dir überlassen. Die zweite Darstellung mit der Eulerschen Zahl findest du aber häufig im Zusammenhang mit Differentialgleichungen
in der Physik.
Hinweis: Ob jetzt für die Variable der Zeit der Buchstabe  ,
,  oder irgendein anderer verwendet wird, ist egal. Ebenso ist die Abkürzung für die Population (ob B, f oder irgendwas anderes), sowie für den Anfangsbestand oder den Wachstumsfaktor unwichtig. Was wirklich für exponentielles Wachstum zählt, ist, dass die Variable im Exponenten steht.
oder irgendein anderer verwendet wird, ist egal. Ebenso ist die Abkürzung für die Population (ob B, f oder irgendwas anderes), sowie für den Anfangsbestand oder den Wachstumsfaktor unwichtig. Was wirklich für exponentielles Wachstum zählt, ist, dass die Variable im Exponenten steht.
Wenn ich dir also folgende Formel gebe

und dich frage, ob das nun exponentielles Wachstum ist oder nicht, wie lautet dann deine Antwort? Die Antwort ist Ja, denn die Variable „Sonne“ steht im Exponenten.
Beispiel: Exponentielles Wachstum Biologie
Lass uns ein Beispiel aus der Biologie betrachten. Hierzu nehmen wir an, dass wir eine Bakterienkultur untersuchen, die zu Beginn 150 Bakterien enthält. Die Bakterienanzahl verdoppelt sich alle drei Stunden. Die Vermehrung der Bakterien soll durch exponentielles Wachstum modelliert werden. Die Formel dazu lautet
 .
.
Den Anfangsbestand zu bestimmen ist leicht. Wir haben zu Beginn 150 Bakterien, daher ist  . Aber wie wird der Wachstumsfaktor bestimmt? Das schauen wir uns weiter unten in Form einer Aufgabe genauer an. Wenn wir diese Funktion zeichnen lassen, erhalten wir den folgenden Graphen.
. Aber wie wird der Wachstumsfaktor bestimmt? Das schauen wir uns weiter unten in Form einer Aufgabe genauer an. Wenn wir diese Funktion zeichnen lassen, erhalten wir den folgenden Graphen.
Der Graph verläuft wie gewünscht: Er beginnt bei 150, nach 3 Stunden verdoppelt sich die Bakterienanzahl auf 300, nach weiteren 3 Stunden verdoppelt sie sich auf 600 und so weiter.
Rekursive Darstellung
Gehen wir zurück zu unserem Beispiel mit der Papierdicke. Wie konnten wir noch einmal die Papierdicke nach einer Faltung bestimmen, wenn wir die Papierdicke vor der Faltung wussten? Wir nahmen die Papierdicke vor der Faltung und multiplizierten diese mit dem Faktor 2. Es gilt also
Papierdicke nach der Faltung = 2 mal Papierdicke vor der Faltung.
Diese Vorgehensweise, dass man einen „späteren“ Wert durch einen „vorherigen“ Wert bestimmt, heißt rekursiv.
Wenn wir jetzt anstatt der Anzahl an Faltungen wieder die Zeit  als Variable betrachten, dann gilt formal
als Variable betrachten, dann gilt formal
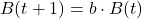
In Worten gefasst, besagt die Formel
Nimm die Population zu einem bestimmten Zeitpunkt t, multipliziere sie mit einem Faktor b und du erhältst die Population zu einem späteren Zeitpunkt t + 1.
Wenn du zum Beispiel die Population zum Zeitpunkt 3 wissen möchtest, dann nimmst du die Population zum Zeitpunkt 2 und multiplizierst sie mit dem Faktor b. Der Faktor b ändert sich nicht mit der Zeit.
Beispiel: Zinseszins
Nehmen wir an, dass du am Anfang des Monats ein Taschengeld von 50€ bekommen hast. Mit dem Taschengeld, das du dir bisher verdient hast, hast du bereits alles gekauft, was du jemals besitzen wolltest. Daher legst du die 50€ an.
Dabei erinnerst du dich an deinen sehr großzügigen Verwandten, der dir schon einmal angeboten hatte, dein Geld für dich anzulegen. Jeden Monat würdest du 10% mehr Geld bekommen als du am Anfang des Monats hattest. Du weißt nicht viel von Geldanlagen, aber du kennst die rekursive Darstellung für exponentielles Wachstum. Bevor du also deinem Verwandten zusagst, rechnest du aus, wie viel du am Ende des Jahres besitzen würdest.
Erstmal überlegst du dir, um welchen Faktor dein Geld jeden Monat steigt. Du weißt, dass 10% gerade 0,1 sind. Da du 10% mehr bekommst, berechnest du den Faktor zu 1 + 0,1 = 1,1. Jetzt kennst du den Wachstumsfaktor b und beginnst eine Tabelle aufzunehmen. Zum Zeitpunkt  hast du 50€. Zum späteren Zeitpunkt
hast du 50€. Zum späteren Zeitpunkt  hast du
hast du
 €.
€.
Am Ende des nächsten Monats hast du
 €.
€.
Du führst diesen Prozess immer weiter und füllst deine Tabelle aus:
| Monat | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Geld | 50€ | 55€ | 60,5€ | 66,55€ | 73,21€ | 80,53€ | 88,58€ | 97,44€ | 107,18€ | 117,9€ | 129,69€ | 142,66€ |
Am Ende des Jahres hast du also 142,66€. Dir gefällt diese Summe und daher sagst du dem Angebot deines Verwandten zu.
Die Änderungsrate des exponentiellen Wachstums
Wenn du die Population zum Zeitpunkt  nimmst und von ihr die Population zum Zeitpunkt
nimmst und von ihr die Population zum Zeitpunkt  abziehst, erhältst du die absolute Änderungsrate
abziehst, erhältst du die absolute Änderungsrate  . Es gilt also
. Es gilt also
 .
.
Wichtig ist zu erkennen, dass die absolute Änderungsrate direkt proportional zur Population selbst ist. Das ist eine wichtige Eigenschaft für exponentielles Wachstum. Das konnten wir beim Beispiel der Bakterienkultur erkennen: Je mehr Bakterien vorhanden sind, umso stärker wächst ihre Anzahl von einem Zeitpunkt zu einem späteren Zeitpunkt. Bei der ersten Verdopplung beispielsweise kamen nur 150 Bakterien hinzu, während es bei der zweiten Verdopplung bereits 300 waren.
Nimmst du die absolute Änderungsrate und dividierst sie durch die Population, erhältst du die sogenannte relative Änderungsrate
 .
.
Im Gegensatz zur absoluten Änderungsrate ist die relative Änderungsrate bei exponentiellem Wachstum konstant.
Exponentieller Zerfall
Bisher haben wir den Wachstumsfaktor nur als Parameter kurz erwähnt. In diesem Abschnitt wollen wir uns seine Bedeutung etwas näher ansehen.
Wenn der Wachstumsfaktor b größer als 1 ist, dann wächst die Population mit der Zeit. Die Bezeichnung „Wachstumsfaktor“ beschreibt daher recht anschaulich diese Situation. Je größer der Wachstumsfaktor ist, umso schneller wächst die Population. Graphisch spiegelt sich das in Form einer steileren Kurve wider. Diese Beobachtung soll das folgende Bild illustrieren. Für alle vier Funktionen wurde die Gleichung

verwendet, wobei der Wachstumsfaktor  die im Bild dargestellten Werte annimmt.
die im Bild dargestellten Werte annimmt.
Wenn der Wachstumsfaktor aber zwischen 0 und 1 liegt, dann werden die Werte immer kleiner. Die Bezeichnung „Wachstumsfaktor“ passt in dieser Situation der exponentiellen Abnahme beziehungsweise des exponentiellen Zerfalls nicht mehr. Daher findest du stattdessen oft die Bezeichnung Abnahmefaktor. Die folgende Grafik soll das veranschaulichen.
Exponentielles Wachstum Aufgaben
In diesem Abschnitt rechnen wir gemeinsam drei Aufgaben aus. In der ersten Aufgabe werden wir den Wachstumsfaktor bestimmen, in der Zweiten ermitteln wir, ob eine gegebene Population exponentiellem Wachstum gehorcht und in der dritten Aufgabe haben wir das Modell für exponentielles Wachstum gegeben und interessieren uns für bestimmte Kenngrößen.
Aufgabe 1: Berechnung des Wachstumsfaktors
Du untersuchst eine Bakterienkultur. Am Anfang sind 150 Bakterien enthalten. Alle 3 Stunden soll sich die Bakterienanzahl verdoppeln. Bestimme den Wachstumsfaktor und schreibe die vollständige Funktion für exponentielles Wachstum auf.
Lösung: Aufgabe 1
Du weißt, dass zu Beginn 150 Bakterien vorhanden sind. Es gilt also  . Nach 3 Stunden hat sich die Anzahl verdoppelt. Du hast also
. Nach 3 Stunden hat sich die Anzahl verdoppelt. Du hast also
 .
.
Diese Gleichung musst du nun nach  umstellen. Dafür teilst du zunächst beide Seiten durch 150 und erhältst
umstellen. Dafür teilst du zunächst beide Seiten durch 150 und erhältst
 .
.
Wende jetzt auf beiden Seiten den natürlichen Logarithmus an und verwende die Rechenregel  .
.
 .
.
Teile anschließend beide Seiten durch 3 und wende die e-Funktion an.
 .
.
Damit hast du alle Parameter bestimmt und die Funktion für exponentielles Wachstum lautet
 .
.
Aufgabe 2: Ermitteln, ob exponentielles Wachstum vorliegt
Du hast folgende Tabelle gegeben, welche das Wachstum einer Population mit der Zeit t darstellen soll
| Zeit t | Population B(t) |
| 0 | 125 |
| 1 | 168,75 |
| 2 | 227,81 |
| 3 | 307,55 |
| 4 | 415,19 |
| 5 | 560,50 |
(a) Bestimme, ob sich diese Population durch exponentielles Wachstum modellieren lässt.
(b) Falls exponentielles Wachstum vorliegt, bestimme alle Parameter und schreibe die Funktion auf.
Lösung: Aufgabe 2
(a) Für exponentielles Wachstum ist es charakteristisch, dass zwischen zwei Populationswerten zu zwei benachbarten Zeitpunkten immer der gleiche Faktor herrscht. Um das für die gegebene Population zu überprüfen, füllst du folgende Tabelle aus
| Zeitpunkte |  |
| t = 0 und 1 | 1,35 |
| t = 1 und 2 | 1,35 |
| t = 2 und 3 | 1,35 |
| t = 3 und 4 | 1,35 |
| t = 4 und 5 | 1,35 |
Du erkennst, dass zwischen zwei benachbarten Zeitpunkten immer der gleiche Faktor vorliegt. Daher lässt sich die Population durch exponentielles Wachstum modellieren.
(b) Die Parameter lassen sich leicht bestimmen. Zum Zeitpunkt  ist die Population 125. Somit ist
ist die Population 125. Somit ist  . Der Wachstumsfaktor entspricht 1,35. Die Funktion für exponentielles Wachstum lautet daher
. Der Wachstumsfaktor entspricht 1,35. Die Funktion für exponentielles Wachstum lautet daher
 .
.
Aufgabe 3: Berechnen bestimmter Kenngrößen
Die folgende Funktion ist gegeben
 .
.
(a) Handelt es sich hierbei um eine Funktion, die exponentielles Wachstum modelliert?
(b) Falls exponentielles Wachstum vorliegt, bestimme die Parameter A und b der allgemeinen Gleichung.
(c) Falls exponentielles Wachstum vorliegt, bestimme den Zeitpunkt  zu dem sich die Population verdoppelt hat.
zu dem sich die Population verdoppelt hat.
Lösung: Aufgabe 3
(a) Die gegebene Funktion stellt exponentielles Wachstum dar, da die Variable  im Exponenten vorkommt und die Basis größer als 1 ist.
im Exponenten vorkommt und die Basis größer als 1 ist.
(b) Der Anfangsbestand A gibt die Population zum Zeitpunkt Null an. Es gilt also
 .
.
Der Wachstumsfaktor b entspricht gerade der Basis der Exponentialfunktion. Damit ist  .
.
(c) Zum Zeitpunkt  gilt
gilt
 .
.
Diese Gleichung muss nach  umgestellt werden. Dazu teilst du beide Seiten durch 35 und wendest den natürlichen Logarithmus an
umgestellt werden. Dazu teilst du beide Seiten durch 35 und wendest den natürlichen Logarithmus an
 .
.
Aufgelöst nach  erhältst du
erhältst du
 .
.
Exponentielles Wachstum — häufigste Fragen
(ausklappen)
Exponentielles Wachstum — häufigste Fragen
(ausklappen)-
Was ist das wichtigste Merkmal von exponentiellem Wachstum?Das wichtigste Merkmal von exponentiellem Wachstum ist, dass sich die Populationswerte zwischen zwei benachbarten Zeitpunkten immer um denselben Faktor vervielfachen. Dadurch werden die absoluten Zuwächse mit der Zeit größer und das Wachstum ist nicht beschränkt. Zum Beispiel verdoppelt sich beim Papierfalten die Dicke nach jeder Faltung.
-
Wie erkenne ich exponentielles Wachstum in einer Tabelle?Exponentielles Wachstum erkennst du in einer Tabelle daran, dass der Quotient
 für alle benachbarten Zeitpunkte konstant ist. Konkret: Bei der Papierdicke gilt
für alle benachbarten Zeitpunkte konstant ist. Konkret: Bei der Papierdicke gilt  und auch
und auch  , also ist der Faktor jedes Mal gleich.
, also ist der Faktor jedes Mal gleich.
-
Was bedeuten Anfangsbestand A und Wachstumsfaktor b in B(t)?In
 ist
ist  der Anfangsbestand, also die Populationsgröße zum Zeitpunkt
der Anfangsbestand, also die Populationsgröße zum Zeitpunkt  . Der Wachstumsfaktor
. Der Wachstumsfaktor  ist der konstante Faktor, mit dem die Population pro Zeitschritt multipliziert wird. Zum Beispiel gilt bei
ist der konstante Faktor, mit dem die Population pro Zeitschritt multipliziert wird. Zum Beispiel gilt bei  :
:  und
und  .
.
-
Wie komme ich von A mal b hoch t zu A mal e hoch Lambda mal t?Von
 kommst du zu
kommst du zu  , indem du
, indem du  setzt. Dann wird die Basis
setzt. Dann wird die Basis  durch die Basis
durch die Basis  ersetzt und die Wachstumsinformation steckt in
ersetzt und die Wachstumsinformation steckt in  . Konkret wird aus
. Konkret wird aus  die Form
die Form  .
.
-
Wann ist es exponentieller Zerfall statt exponentielles Wachstum?Exponentieller Zerfall liegt vor, wenn der Faktor
 zwischen 0 und 1 liegt, weil die Werte dann von Schritt zu Schritt kleiner werden. In diesem Fall heißt
zwischen 0 und 1 liegt, weil die Werte dann von Schritt zu Schritt kleiner werden. In diesem Fall heißt  oft Abnahmefaktor. Exponentielles Wachstum liegt dagegen bei
oft Abnahmefaktor. Exponentielles Wachstum liegt dagegen bei  vor, weil die Population dann zunimmt.
vor, weil die Population dann zunimmt.
Beschränktes Wachstum
Das exponentielle Wachstum ist unbeschränkt. Die Population kann damit beliebig große oder kleine Werte annehmen. Anders ist das beim beschränkten Wachstum. Hierbei gibt es eine natürliche Schranke, die die Population nach unten oder nach oben hin begrenzt. Schau dir unbedingt auch unser Video zum beschränkten Wachstum an, um alles Wichtige über die Wachstumsprozesse zu erfahren!




