Wichtig ist also, dass jedes Element im Definitionsbereich (x-Achse) nur ein zugehöriges Element im Wertebereich (y-Achse) haben darf. Das Ergebnis von Funktionen muss also immer eindeutig sein.

Lineare Funktionen

im Videozur Stelle im Video springen

(01:06)

Lineare Funktionen sind Geraden im Koordinatensystem.

Funktionsgleichung für lineare Funktionen

f(x) = m · x + b

m gibt ihre Steigung an und b den y-Achsenabschnitt.

Um die Steigung zu berechnen , verwendest du das Steigungsdreick mit der Formel

$m =\frac{y_2 -y_1}{x_2 -x_1}$

lineare Funktionen, Gerade, Steigungsdreieck, Steigung, y-Achsenabschnitt, mx+b, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Lineare Funktionen zeichnen

Wenn der Schnittpunkt zweier Geraden gefragt ist, setzt du die beiden linearen Funktionen gleich.

Quadratische Funktionen

im Videozur Stelle im Video springen

(01:29)

Der Funktionsgraph von quadratischen Funktionen heißt Parabel. Die einfachste quadratische Funktion ist die Normalparabel f(x) = x².

Funktionsgleichung für quadratische Funktionen

f(x) = ax²+bx+c

Parabeln, Scheitelpunktform, quadratische Gleichungen, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Quadratische Gleichungen und Parabeln

Quadratische Funktionen können auch in anderen Formen gegeben sein.

Andere Funktionsgleichungen für quadratische Funktionen

f(x) = a(x-d)²+e Scheitelpunktform mit Scheitelpunkt S(d|e)

f(x) = a(x-x₁)(x-x₂) faktorisierte Form mit Nullstellen x₁ und x₂

Der Scheitelpunkt ist der höchste oder tiefste Punkt der Parabel.

f(x) = 0,5(x-2)²+1 liegt in Scheitelpunktform vor
f(x) = -x²+2x-1 ist eine Parabel in Normalform
f(x) = (x-6)(x-10) liegt in faktorisierter Form vor

Funktionsgraphen können zwei, eine oder keine Nullstellen haben. Um die Nullstellen zu berechnen , verwendest du die Mitternachtsformel oder die pq Formel .

Willst du den Scheitelpunkt bestimmen, bringst du die Funktionsgleichung mittels quadratischer Ergänzung auf die Scheitelpunktform .

Potenzfunktionen

im Videozur Stelle im Video springen

(01:51)

Potenzfunktionen unterscheidest du danach, ob sie einen positiven oder negativen, geraden oder ungeraden Exponenten haben.

Funktionsgleichung der Potenzfunktionen

f(x) = a · x ⁿ

Potenzfunktionen, Parabeln, kubische Funktion, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Funktionsgraphen von Potenzfunktionen

f(x) = x² ist die Normalparabel
f(x) = 0,1x³ ist eine Potenzfunktion 3. Grades
f(x) = 2x^-1 ist eine Potenzfunktion mit negativem Exponenten

Wurzelfunktion

im Videozur Stelle im Video springen

(02:29)

Wurzelfunktionen können als Potenzfunktionen mit einem Bruch als Exponenten interpretiert werden.

Funktionsgleichung von Wurzelfunktionen:

(Quadrat-)Wurzel: $\sqrt{x} = x^\frac{1}{2}$

n-te Wurzel: $\sqrt[n]{x} = x^\frac{1}{n}$

Je größer n ist, desto flacher verläuft der Graph ab x = 1.

Wurzelfunktionen, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Funktionsgraph verschiedener Wurzelfunktionen

Aufpassen musst du hier beim Definitionsbereich! Wurzelfunktionen mit geradem Wurzelexponent sind nur für Zahlen $x \ge 0$ definiert. Das heißt, du darfst keine negativen Werte in die Funktion einsetzen!

Ganzrationale Funktionen und Polynome

im Videozur Stelle im Video springen

(02:13)

Die Funktionsgleichung einer ganzrationalen Funktion enthält stets ein Polynom , weswegen sie manchmal auch als Polynomfunktion bezeichnet wird.

Funktionsgleichung für ganzrationale Funktionen

$f(x)=a_nx^n+a_{n-1}x^{n-1}+\ldots+a_2x^2+a_1x+a_0$

Je nach Grad der Funktion, erhältst du hier Funktionsgraphen, die einer Parabel oder einer Funktion 3. Grades ähneln. Die Funktion hat maximal so viele Nullstellen, wie das größte n der Funktion.

ganzrationale Funktionen, Polynomfunktion, Funktion 3. Grades, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Ganzrationale Funktionen 3. und 4. Grades

f(x) = 0,5x³+x²-1,5x-2 ist eine ganzrationale Funktion 3. Grades
g(x) = 0,5x⁴-3x³+5x²-2x+0,5 ist eine ganzrationale Funktion 4. Grades

Merke: Potenzfunktionen, Polynomfunktionen und Wurzelfunktionen aller Art werden unter dem Überbegriff Rationale Funktionen zusammengefasst!

Gebrochen rationale Funktionen

im Videozur Stelle im Video springen

(02:56)

Gebrochen rationale Funktionen bestehen immer aus einem Bruch mit Polynomen im Zähler und im Nenner. Die allgemeine Funktionsgleichung lautet hier:

Allgemeine Funktionsgleichung einer gebrochen rationalen Funktion

$f(x)=\cfrac{p(x)}{q(x)}=\cfrac{a_nx^n+a_{n-1}x^{n-1}+\ldots+a_2x^2+a_1x+a_0}{b_mx^m+b_{m-1}x^{m-1}+\ldots+b_2x^2+b_1x+b_0}$

gebrochen rationale Funktionen, gebrochenrationale Funktionen, Asymptote, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Funktionsgraph gebrochen rationaler Funktionen

Der Funktionsgraph einer gebrochen rationalen Funktion sieht je nach Zählergrad und Nennergrad verschieden aus. Kennzeichnend ist dabei jedoch stets die senkrechte Asymptote an den Polstellen , die du als Nullstelle des Nenners berechnest. Die anderen Asymptoten der Funktion kannst du mithilfe von Grenzwertberechnungen bestimmen.

Exponentialfunktion und e Funktion

im Videozur Stelle im Video springen

(03:23)

Eine Exponentialfunktion stellt exponentielles Wachstum dar, wie es in der Natur beispielsweise bei der Entwicklung einer Bakterienkultur oder beim Zerfall eines radioaktiven Elements vorkommt.

Funktionsgleichung der Expoentialfunktion und der e Funktion

Exponentialfunktion: f(x) = a · b^x mit Basis b und Anfangswert a

e Funktion: f(x) = e^x mit Basis e = 2,7182…

Eine besondere Rolle spielt dabei die e-Funktion (auch natürliche Exponentialfunktion) zur Basis e = 2,7182…

e Funktion, Exponentialfunktion, exponentielles Wachstum, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Exponentialfunktion und e Funktion

f(x) = e^x ist der Funktionsgraph der e Funktion
f(x) = 0,5 · 2^x ist eine steigende Exponentialfunktion
f(x) = 3 · 0,25^x ist eine fallende Exponentialfunktion

Merke: Die Basis b muss hier immer ungleich Null sein!

Logarithmusfunktion und ln Funktion

im Videozur Stelle im Video springen

(03:49)

Wenn du eine Exponentialfunktion nach x auflösen möchtest, benötigst du ihre Umkehrfunktion, die Logarithmusfunktion . Auch hier gibt es den Sonderfall der ln-Funktion , was der Umkehrung der e Funktion entspricht.

Logarithmusfunktion und ln Funktion

$f(x)=\log _b(x)$

$f(x)=\ln (x)$

Logarithmus, log, ln, log(x), ln(x), Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Logarithmusfunktion und ln Funktion

$f(x)=\ln (x)$ (blau) ist die normale ln Funktion
$f(x)=\log(x)$ (grün) ist der Zehnerlogarithmus, d.h. der Logarithmus zur Basis 10
$f(x)=\log _2(x)$ (lila) ist der Logarithmus zur Basis 2

Merke: Klassischerweise bezeichnet 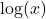$\log(x)$ den Zehnerlogarithmus oder dekadischen Logarithmus, das heißt den Logarithmus zur Basis 10. $\ln(x)$ nennt man hingegen den natürlichen Logarithmus, also den Logarithmus zur Basis e: $\log _e(x)=\ln (x)$ .

Für die Logarithmus-Funktion gibt es verschiedene Rechenregeln, die du kennen solltest. Ausführlich erklären wir sie dir im Artikel Logarithmus Regeln . Es gilt:

Logarithmus Regeln

$\log _a(x) + \log _a(y) = \log _a(x \cdot y)$

$\log _a(x) - \log _a(y)= \log _a(\cfrac{x}{y})$

$\log _a(x^y)=y \cdot log_a(x)$

$\log_a(x)=\cfrac{\log_a(x)}{\log_a(b)}$

Trigonometrische Funktionen

im Videozur Stelle im Video springen

(04:09)

Die drei wichtigsten trigonometrischen Funktionen sind die Sinusfunktion , die Cosinusfunktion und der Tangens . Sie alle zeichnen sich durch ihre Periodizität aus, weil sie sich überall auf dem Zahlenstrahl gleich verhalten wie im Intervall [0, $\pi$ ].

Funktionsgleichung der trigonometrischen Funktionen

f(x) = sin(x)

f(x) = cos(x)

f(x) = tan(x)

Sinus, Cosinus, sin(x), cos(x), Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Sinus und Cosinus

Manipulation von Grundfunktionen

Du kannst aus einer alten Funktion f(x) eine neue Funktion g(x) machen! Dazu veränderst du einfach die alte Funktion: Du kannst sie zum Beispiel verschieben, stauchen, strecken oder spiegeln. Das nennst du auch manipulieren.

Dabei ändern sich auch die Definitionsmenge D (Werte, die du für x einsetzen darfst) und die Wertemenge W (Werte, die du für y einsetzen darfst). Den neuen Definitions- und Wertebereich nennst du dann D_g und W_g. Du sagst dann:

Der Graph g entsteht aus dem Graphen von f durch…

	g(x)	D_g	W_g
Verschiebung in y-Richtung um e	f(x) + e	D	e + W
Verschiebung in x-Richtung um d	f(x + d)	-d + D	W
Streckung (a > 1) oder Stauchung (0 < a < 1) in y-Richtung mit dem Faktor a	a · f(x)	D	a · W
Stauchung (b > 1) oder Streckung (0 < b < 1) in x-Richtung mit dem Faktor 1/b	f(b · x)	1/b · D	W
Spiegelung an der y-Achse	f(- x)	D	-W
Spiegelung an der x-Achse	– f(x)	D_f	-W_f

Du kannst dir folgendes merken:

Bei Änderungen innerhalb der Funktion f(x – c)

ändert sich der Definitionsbereich
bleibt der Wertebereich gleich

Bei Änderungen außerhalb der Funktion f(x) + c

bleibt der Definitionsbereich gleich
ändert sich der Wertebereich

Wie solche Veränderungen genau funktionieren, siehst du jetzt!

Verschiebung, Streckung, Stauchung und Spiegelung von Funktionen

im Videozur Stelle im Video springen

(04:26)

Schau dir einzelne Beispiele an, bei der quadratische Funktionen im Koordinatensystem verändert werden. Analog funktioniert das auch für alle anderen Funktionstypen.

Verschiebung in y-Richtung

Am einfachsten ist es, wenn du den Graphen einer beliebigen Funktion in Koordinatensystem in y-Richtung nach oben oder nach unten verschiebst. Dazu addierst du den Parameter e zur Funktion f(x).

Verschiebung einer Funktion in y-Richtung

f(x)+e

Verschiebung in y-Richtung, Parabel nach oben/unten verschoben, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Verschiebung einer Parabel in y-Richtung

f(x)=x² ist die Normalparabel
f(x)=x² +2 ist um 2 nach oben verschoben
f(x)=x² -1 ist um 1 nach unten verschoben

Verschiebung in x-Richtung

Wenn du eine Funktion in x-Richtung, das heißt nach links oder nach rechts verschieben willst, musst du den Parameter d direkt in die Funktionsgleichung einfügen. Hier berechnest du somit

Verschiebung einer Funktion in x-Richtung

f(x-d)

Verschiebung nach rechts/links, Verschiebung in x-Richtung, Verschiebung Parabel, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Verschiebung einer Parabel in x Richtung

f(x)=x² ist eine Normalparabel
f(x)=(x+2)² ist um 2 nach links verschoben
f(x)=(x-3)² ist um 3 nach rechts verschoben

Streckung und Stauchung

Zusätzlich zur Verschiebung in beide Richtungen kannst du auch beeinflussen, wie steil die Funktion verläuft. Mithilfe eines Parameters a kann sie gestreckt beziehungsweise gestaucht werden, je nachdem ob a>1 oder a<1 ist. Je größer der betragsmäßige Wert von a ist, desto steiler wird der Funktionsgraph, je näher der Wert bei Null liegt, desto langsamer steigt die Funktion.

Merke: Der Vorfaktor a muss immer ungleich Null sein, da du sonst das konstante Nullpolynom erhältst!

Streckung oder Stauchung einer Funktion

a · f(x)

Streckung Parabel, Parabel, gestauchte Parabel, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Streckung und Stauchung einer Parabel

f(x)=x²ist eine Normalparabel
f(x)=2x²
f(x)=0,25x²
f(x)=-0,5x²

Spiegelung

Im Allgemeinen ist das Thema Spiegelung eng mit der Symmetrie von Funktionsgraphen verwandt. Wenn eine Funktion achsensymmetrisch ist, kannst du ihren Funktionsgraphen an der y-Achse spiegeln. Dann gilt für alle x-Werte aus dem Definitionsbereich

f(x)=f(-x).

Ein typisches Beispiel dafür sind die Parabeln, die – sofern sie nicht in x-Richtung verschoben sind- immer achsensymmetrisch zum Ursprung sind. Eine Funktion dritten Grades ist im Gegensatz dazu punktsymmetrisch zum Ursprung, das heißt

-f(x)=f(-x).

Wenn du einen ganzen Funktionsgraphen dahingegen an der x-Achse spiegeln möchtest, musst du das Vorzeichen des Vorfaktors a anpassen. Dann erhältst du eine ganz neue Funktion, was du auch an der hellblauen Parabel im obigen Bild sehen kannst.

Spiegelung einer Funktion an der x-Achse

– f(x)

Alternativ kannst du die verschiedenen Einflüsse der einzelnen Parameter auch an den Wurzelfunktionen sehen. Im Bild sind die einzelnen Verschiebungen/Streckungen/Stauchungen nochmals zusammengefasst.

Verschiebung, Streckung, Stauchung, Wurzelfunktion, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Zusammenfassung: Verschiebung, Streckung, Stauchung

Betragsfunktion

Die Betragsfunktion f(x)=|x| ist eine wichtige Funktion in der Mathematik. Sie gibt an, wie weit eine Zahl auf dem Zahlenstrahl von der Null entfernt ist und wird deswegen zur Abstandsberechnung verwendet. Die Betragsfunktion besteht aus zwei Halbgeraden, die sich am Ursprung treffen und ist achsensymmetrisch zur y-Achse. Sie ist die Stammfunktion der Signumfunktion und hat die folgende Funktionsgleichung:

Funktionsgleichung der Betragsfunktion

$|x|=\begin{cases} x \quad \quad \quad \mbox{f\"ur} \quad x>0\\ -x \quad \quad \mbox{f\"ur} \quad x<0 \end{cases}$

Wie du an ihrem Funktionsgraph sehen kannst, hat sie einen Knick im Ursprung, was bedeutet, dass sie dort nicht differenzierbar ist.

Betrag, Betragfunktion, Betragsfunktion , Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Betragsfunktion

Signumfunktion

Die Ableitung der Betragsfunktion ist die Signumfunktion. Sie gibt dir das Vorzeichen einer Zahl an, weswegen sie manchmal auch als Vorzeichenfunktion bezeichnet wird. Ihr Wertebereich enthält nur die Zahlen 0, 1 und -1, das heißt $\mathbb{W}=\{-1,0,1\}$ . Im Ursprung ist diese Funktion nicht stetig, sondern hat einen Sprung, weswegen man hier auch von abschnittsweise definierten Funktionen spricht.

Funktionsgleichung der Signumsfunktion

$\text{sgn}(x)= \begin{cases} 1 \quad \quad \quad \mbox{f\"ur} \quad x>0\\ 0 \quad \quad \quad \mbox{f\"ur} \quad x=0\\ -1 \quad \quad \mbox{f\"ur} \quad x<0\end$

Signumfunktion, Vorzeichenfunktion, sign(x), sgn(x), Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Signumfunktion sgn(x)

Umkehrfunktionen

Viele Funktionen besitzen eine Umkehrfunktion , mit der man sie sozusagen rückgängig machen kann. Ob eine Umkehrfunktion existiert, hängt davon ab, ob die ursprüngliche Funktion stetig und streng monoton steigend oder fallend ist. Solche Funktionen heißen auch bijektiv und werden beispielsweise bei der Berechnung von Rotationskörpern regelmäßig gebraucht.

Schreibweise für Umkehrfunktionen

$f^{-1}(x)$

Merke: $f^{-1}(x)$ $\neq$ $\cfrac{1}{f(x)}$ !

Für viele Funktionen gibt es eine Umkehrfunktion nur dann, wenn du den Definitionsbereich einschränkst, sodass die Funktionen in diesem Intervall streng monoton sind. Das typische Beispiel hierfür sind die quadratischen Funktionen auf $\mathbb{R}^+$ , die mithilfe der Wurzelfunktion umkehrbar werden.

$\mathbb{R}_0^+$ $\rightarrow$ $\mathbb{R}_0^+$ mit f(x)=x^2

$f^{-1}:$ $\mathbb{R}_0^+$ $\rightarrow$ $\mathbb{R}_0^+$ mit $f^{-1}(x)=\sqrt{x}$

Um die Umkehrfunktion zu berechnen, gehst du folgendermaßen vor:

Schritt 1: Löse die Funktion f(x)=y nach x auf
Schritt 2: Vertausche die beiden Variablen x und y

Wenn du beispielsweise die Umkehrfunktion von $f(x)=2\sqrt{x+8}$ berechnen willst, dann löst du diese Gleichung nach x auf:

$y=2\sqrt{x+8}$ $\bigg| \div 2$

$\frac{y}{2} = \sqrt{x+8}$ $\bigg| ^2$

$\left(\frac{y}{2}\right)^2 = x+8$ $\bigg| -8$

$\left(\frac{y}{2}\right)^2-8= x$

Jetzt vertauschen wir x und y und erhalten $f^{-1}(x)=\frac{1}{4}x^2-8$ .

Graphisch kannst du eine Umkehrfunktion stets als Spiegelung an der Winkelhalbierenden interpretieren.

Funktion, Umkehrfunktion, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Funktionen und ihre Umkehrfunktionen

Verkettete Funktionen

Zuletzt noch ein paar Informationen zu den verketteten Funktionen. Hier handelt es sich um Verknüpfungen einzelner Funktionen, die du sozusagen nacheinander anwenden musst. Hat eine verkettete Funktion die Form f(g(x)), so berechnest du zuerst g(x) und setzt das Ergebnis davon in f(x) ein. In den meisten Fällen wird dir bei der Berechnung gar nicht auffallen, dass du es mit verketteten Funktionen zu tun hast, lediglich beim Ableiten von verketteten Funktionen und bei der Integralrechnung gelten hier besondere Regeln.

Funktionen Grundlagen

im Videozur Stelle im Video springen

(00:40)

Um Funktionen zu untersuchen und ihre Eigenschaften zu verstehen, gibt es verschiedene Möglichkeiten und Grundlagen, die du kennen solltest. Dabei wird in die Begriffe Funktion, Funktionsgleichung und Funktionsgraph unterschieden.

Funktionsgleichung

Die Funktionsgleichung einer Funktion f bezeichnet die Abbildungsvorschrift. Sie gibt dir an, was genau du berechnen musst. Ein Beispiel dafür ist

$f: x\mapsto \frac{1}{2}x^2-2x+3$ ,

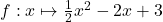wobei die Funktionsgleichung $f(x)=\frac{1}{2}x^2-2x+3$ lautet.

Oft musst du die Funktionsgleichung aufstellen, wenn du konkrete Punkte gegeben hast. Hierzu gibt es einfache Beispiele, wie die Bestimmung der Funktionsgleichung einer Geraden durch zwei Punkte, es kann aber auch deutlich komplizierter werden, wenn du beispielsweise in der induktiven Statistik eine Regressionsgleichung aufstellen sollst.

Merke: Streng formal besteht ein Unterschied zwischen der Funktion f und ihrer Funktionsgleichung f(x)=2x+3.

Wertetabelle

Um konkrete Aussagen über eine Funktion treffen zu können, bietet sich oftmals eine Wertetabelle an. Hier setzt du verschiedene Funktionswerte x in die Funktionsgleichung ein und hältst das Ergebnis tabellarisch fest. Am besten zeigen wir dir das am Beispiel einer linearen Funktion f mit Funktionsgleichung f(x)=1,2x mit der du beispielsweise den Zusammenhang zwischen den Kosten und der Anzahl an Schokoladentafeln zum Preis 1,20€ darstellen kannst.

Anzahl	0	1	2	3	4	5	6	7	8	9	10
Preis	0	1,20€	2,40 €	3,60 €	4,80 €	6,00 €	7,20 €	8,40€	9,60 €	10,80 €	12,00€

Funktionsgraph im Koordinatensystem

Um dir den Verlauf einer Funktion vorzustellen, bietet es sich an, die einzelnen Punkte der Wertetabelle in einem Koordinatensystem zu veranschaulichen. Verbindest du die Punkte, hast du den Funktionsgraphen der Funktion gezeichnet.

lineare Funktion, Gerade, Wertetabelle, Funktion, Funktionen, Funktion, Funktionen Mathe, Funktionstypen, Mathematische Funktion, Funktionen Beispiele, Was ist eine Funktion Mathe, Welche Funktionen gibt es, Definition einer Funktion, Funktion x, Was ist Funktion — Funktionsgraph

Ableitung

Mathematische Funktionen brauchst du zum Beispiel um die Veränderungen von Wasserbeständen in Seen oder die Geschwindigkeit von Flugzeugen abzubilden. Dabei spielt auch die Ableitung eine wichtige Rolle. Welche Bedeutung sie in verschiedenen Fällen hat, erklären wir dir hier ! %Verlinken %hab die Tabelle jetzt doch rausgelassen, weil sie ohne Beispiele kaum einen Mehrwert hat und das ja auch nicht der Fokus des Artikels ist

Funktionen Funktionen - Grundlagen

Funktionen Funktionen - fortgeschritten

Funktionen Zuordnungen

Funktionen Lineare Funktionen

Funktionen Quadratische Funktionen

Funktionen Formen von quadratischen Funktionen

Funktionen Trigonometrie

Funktionen Trigonometrische Funktionen

Funktionen Polynome

Funktionen Polynomdivision

Funktionen Rationale Funktionen

Funktionen Exponentialfunktion

Funktionen Logarithmus

Funktionen Fortgeschrittene trigonometrische Funktionen

Funktionen

Funktionen einfach erklärt

Lineare Funktionen

Quadratische Funktionen

Potenzfunktionen

Wurzelfunktion

Ganzrationale Funktionen und Polynome

Gebrochen rationale Funktionen

Exponentialfunktion und e Funktion

Logarithmusfunktion und ln Funktion

Trigonometrische Funktionen

Manipulation von Grundfunktionen

Verschiebung, Streckung, Stauchung und Spiegelung von Funktionen

Verschiebung in y-Richtung

Verschiebung in x-Richtung

Streckung und Stauchung

Spiegelung

Betragsfunktion

Signumfunktion

Umkehrfunktionen

Verkettete Funktionen

Funktionen Grundlagen

Funktionsgleichung

Wertetabelle

Funktionsgraph im Koordinatensystem

Ableitung

Beliebte Inhalte aus dem Bereich Funktionen

Funktionen

Funktionen - Grundlagen

Funktionen

Funktionen - fortgeschritten

Funktionen

Zuordnungen

Funktionen

Lineare Funktionen

Funktionen

Quadratische Funktionen

Funktionen

Formen von quadratischen Funktionen

Funktionen

Trigonometrie

Funktionen

Trigonometrische Funktionen

Funktionen

Polynome

Funktionen

Polynomdivision

Funktionen

Rationale Funktionen

Funktionen

Exponentialfunktion

Funktionen

Logarithmus

Funktionen

Fortgeschrittene trigonometrische Funktionen