Was heißt lineares Wachstum in einer Alltagssituation genau?

Lineares Wachstum in einer Alltagssituation bedeutet, dass sich eine Größe in gleichen Zeitabständen immer um den gleichen Betrag verändert. Dadurch steigt oder fällt die Größe gleichmäßig. Zum Beispiel wächst die Wassermenge in einer Badewanne jede Minute um genau 10 Liter, wenn 10 Liter pro Minute zufließen.

Woran erkenne ich lineares Wachstum an der Änderungsrate a?

Lineares Wachstum erkennst du daran, dass die Änderungsrate a konstant ist, also über die Zeit immer gleich bleibt. Außerdem gilt: Bei ist die Funktion streng monoton steigend (Wachstum), bei streng monoton fallend (linearer Zerfall). Beispiel: „10 cm pro Jahr“ beschreibt eine konstante Änderungsrate.

Wie stelle ich die Funktion N(t) aus Startwert N₀ auf?

Die Funktion stellst du mit auf, wobei der Startwert bei und die konstante Änderungsrate ist. Konkret: Bei m und m/Jahr ergibt sich .

Wie lese ich die Änderungsrate a aus einem Graphen ab?

Die Änderungsrate a liest du aus dem Graphen mit einem Steigungsdreieck als ab. Beispiel: Zwischen A(2,5|17,5) und B(5|25) gilt und , also .

Wie berechne ich die Zeit t aus einer linearen Wachstumsfunktion?

Die Zeit berechnest du, indem du den gewünschten Wert für einsetzt und die Gleichung nach auflöst. Beispiel: Bei und folgt , dann und damit .

Video

Quiz

Hier geht's zum Video „Lineare Funktionen“

Hier geht's zum Video „Steigungsdreieck“

Hier geht's zum Video „Monotonie“

Hier geht's zum Video „Wachstumsprozesse“

Lineares Wachstum

Wichtige Inhalte in diesem Video

Lineares Wachstum einfach erklärt

(00:15)

Änderungsrate mit Graph berechnen

(01:52)

Du willst wissen, was du unter linearem Wachstum verstehen kannst? Hier und im Video erklären wir dir alles, was du dazu wissen musst.

Inhaltsübersicht

Lineares Wachstum einfach erklärt

im Videozur Stelle im Video springen

(00:15)

Lineares Wachstum oder linearen Zerfall hast du dann, wenn sich eine Größe pro gleichbleibenden Zeitabstand immer konstant verändert:

Stell dir vor, du drehst den Wasserhahn der Badewanne auf und es kommen 10 Liter Wasser pro Minute raus. Das ist lineares Wachstum, denn deine Wassermenge verändert sich in der gleichen Zeit immer um die gleiche Menge.

Willst du diesen Vorgang als Funktion darstellen, kannst du eine Geradengleichung mit den folgenden Werten verwenden:

N(t) = N₀ + a • t

N(t): Wassermenge in der Badewanne zu einem bestimmten Zeitpunkt t.
N₀: Startwert der Wassermenge in der Badewanne am Anfang, bevor du den Wasserhahn aufdrehst.
a: Die Änderungsrate, die die Menge an Wasser pro Minute beschreibt

Am Anfang ist die Badewanne leer, deshalb setzt du für N₀ = 0 ein. Die Änderung der Wassermenge pro Minute sind 10 Liter. Also ist a = 10. Setzt du nun beides in die Gleichung ein, kommt folgende Wachstumsfunktion raus:

N(t) = 0 + 10 • t = 10 • t

Eigenschaften von linearem Wachstum

Die Änderungsrate a ist bei linearem Wachstum konstant und entspricht der Steigung des Graphen der linearen Funktion .
a > 0: Die Funktion ist streng monoton steigend . Es handelt sich um lineares Wachstum.
a < 0: Die Funktion ist streng monoton fallend. Es liegt ein linearer Zerfallsprozess vor.

Änderungsrate mit Graph berechnen

im Videozur Stelle im Video springen

(01:52)

Die Änderungsrate einer Wachstumsfunktion kannst du mithilfe eines Steigungsdreiecks berechnen.

Lineare Funktion, Lineares Wachstum, Linearer Wachstumsprozess, Wachstumsfunktion, Lineare Wachstumsfunktion, Wachstum mit Steigungsdreieck, Steigungsdreieck, Steigungsdreieck ablesen, Steigungsdreieck berechnen, Steigung berechnen, konstante Steigung — Steigungsdreieck ablesen

Dafür suchst du dir zum Beispiel die Punkte A(2,5|17,5) und B(5|25) auf der Geraden und zeichnest ein Dreieck ein. Nun musst du Δt und ΔN(t) ablesen. Das Δt steht für die Zeitspanne, in der du das Wachstum beobachtest. Hier geht es von t = 2,5 bis t = 5.

Δt = 5 – 2,5 = 2,5

Den Unterschied zwischen den Werten von N in dieser Zeitspanne beschreibt ΔN(t):

ΔN(t) = N(5) – N(2,5) = 25 – 17,5 = 7,5

Mit diesen beiden Werte kannst du jetzt die Änderungsrate berechnen:

a = 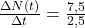$\frac{\Delta N(t)}{\Delta t} = \frac{7,5}{2,5}$ = 3

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Lineare Wachstumsfunktion aufstellen

Zur Vorgehensweise beim Aufstellen einer linearen Wachstumsfunktion kannst du dir folgendes Beispiel anschauen:

Eine Hecke wird in eurem Garten gepflanzt. Sie ist beim Einsetzen 0,5 m hoch und wächst 10 cm pro Jahr. Stelle die lineare Wachstumsfunktion auf. Berechne dann, wie lange es dauert, bis die Hecke 1,5 m hoch ist.

Der Wert der Änderungsrate ist hier schon gegeben. Du erkennst sie an der Formulierung „pro Jahr“. Rechne die cm/Jahr noch in m/Jahr um, damit jede Längeneinheit in Meter angegeben ist.

a = 10 cm/Jahr = 0,1 m/Jahr

Am Anfang hat die Hecke schon 0,5 m. Das bedeutet das N₀ deiner Funktion ist 0,5.

N₀= 0,5 m

Mit diesen Werten kannst du die Funktion für lineares Wachstum aufstellen.

N(t) = N₀ + a • t = 0,5 + 0,1 • t

Du hast die Wachstumsfunktion aufgestellt. Berechne jetzt die Zeit t, die die Hecke braucht, um 1,5 m hoch zu wachsen. Setze dafür N(t) = 1,5 und löse nach t auf.

$\begin{align*}N(t) &= 1,5 \\ 0,5 + 0,1 \cdot t &= 1,5 &| - 0,5 \\ 0,1 \cdot t &= 1 &| : 0,1 \\ \textcolor{orange}{t} &= \textcolor{orange}{10} \end{align*}$

Die Hecke in eurem Garten braucht also 10 Jahre, um 1,5 m hoch zu werden.

Lineares Wachstum — häufigste Fragen

(ausklappen)

Was heißt lineares Wachstum in einer Alltagssituation genau?

Lineares Wachstum in einer Alltagssituation bedeutet, dass sich eine Größe in gleichen Zeitabständen immer um den gleichen Betrag verändert. Dadurch steigt oder fällt die Größe gleichmäßig. Zum Beispiel wächst die Wassermenge in einer Badewanne jede Minute um genau 10 Liter, wenn 10 Liter pro Minute zufließen.
Woran erkenne ich lineares Wachstum an der Änderungsrate a?

Lineares Wachstum erkennst du daran, dass die Änderungsrate a konstant ist, also über die Zeit immer gleich bleibt. Außerdem gilt: Bei ist die Funktion streng monoton steigend (Wachstum), bei streng monoton fallend (linearer Zerfall). Beispiel: „10 cm pro Jahr“ beschreibt eine konstante Änderungsrate.
Wie stelle ich die Funktion N(t) aus Startwert N₀ auf?

Die Funktion stellst du mit $N(t)=N_0+a\cdot t$ auf, wobei der Startwert bei und die konstante Änderungsrate ist. Konkret: Bei $N_0=0{,}5$ m und m/Jahr ergibt sich $N(t)=0{,}5+0{,}1\cdot t$ .
Wie lese ich die Änderungsrate a aus einem Graphen ab?

Die Änderungsrate a liest du aus dem Graphen mit einem Steigungsdreieck als $a=\frac{\Delta N(t)}{\Delta t}$ ab. Beispiel: Zwischen A(2,5|17,5) und B(5|25) gilt $\Delta t=5-2{,}5=2{,}5$ und $\Delta N(t)=25-17{,}5=7{,}5$ , also $a=\frac{7{,}5}{2{,}5}=3$ .
Wie berechne ich die Zeit t aus einer linearen Wachstumsfunktion?

Die Zeit berechnest du, indem du den gewünschten Wert für einsetzt und die Gleichung nach auflöst. Beispiel: Bei $N(t)=0{,}5+0{,}1\cdot t$ und folgt , dann und damit .

Wachstumsprozesse

Prima! Jetzt kennst du dich mit dem linearen Wachstum aus. Willst du noch mehr über die verschiedenen Wachstumsprozesse erfahren? Dann schau direkt im Video dazu vorbei.