Prozentrechnung Aufgaben
Wenn du noch ein bisschen Übung in der Prozentrechnung brauchst, haben wir für dich ein paar Aufgaben vorbereitet. Schaue dir auch unser Video dazu an, um dein Wissen aufzufrischen!
Inhaltsübersicht
Prozentrechnung Aufgaben einfach erklärt
Bevor du dich an die Prozentrechnung Aufgaben machst, solltest du dir noch mal alle wichtigen Formeln ins Gedächtnis rufen. Beim Prozentrechnen wird immer nach dem Grundwert G, dem Prozentwert W und dem Prozentsatz p% gefragt. Du kannst alle Aufgaben mit den drei Prozentformeln lösen:
![Rendered by QuickLaTeX.com \[ \textcolor{magenta}{p\,\%} = \frac{\textcolor{blue}{W}}{\textcolor{orange}{G}} \qquad \textcolor{blue}{W} = \textcolor{magenta}{p\,\%} \cdot \textcolor{orange}{G} \qquad \textcolor{orange}{G} = \frac{\textcolor{blue}{W}}{\textcolor{magenta}{p\,\%}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-cb035aa0b4845b1a043f56fa358663d0_l3.png)
Falls du das im Detail nachschauen magst, musst du dir unbedingt unser Video zur Prozentrechnung ansehen.
Einfache Aufgaben
Fange am Besten mit ein paar Kopfrechenaufgaben an, um mit der Prozentrechnung warm zu werden.
Wie viel ist 10% von 70?
![Rendered by QuickLaTeX.com \[10\,\% \cdot 70 = ?\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-6d0aef676eee8369813ca102630098a7_l3.png)
Wandle um:  und multipliziere 70 mit dem Bruch.
und multipliziere 70 mit dem Bruch.
![Rendered by QuickLaTeX.com \[\frac{1}{10} \cdot 70 = ?\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7f038a651e9c348feb7ed2d3511e1b3c_l3.png)
70 geteilt durch 10 ergibt 7.
![Rendered by QuickLaTeX.com \[\frac{70}{10} = 7\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-893741b59bea560bc1b8f96d7d0ae920_l3.png)
Wie viel ist 75% von 4?
![Rendered by QuickLaTeX.com \[ 75\,\% \cdot 4 = ? \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-869b5a200abd896d5eb923130bb16199_l3.png)
Wandle um:  . Multipliziere 4 mit dem Bruch.
. Multipliziere 4 mit dem Bruch.
![Rendered by QuickLaTeX.com \[ \frac{3}{4} \cdot 4 = 3 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a0145445d048db267fb010f879386f6d_l3.png)
Wie viel ist 25% von 400?
![Rendered by QuickLaTeX.com \[ 25\,\% \cdot 400 = ? \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-393fa344e430064109ab18894139fce5_l3.png)
Wandle um:  . Multipliziere
. Multipliziere  danach mit 400.
danach mit 400.
![Rendered by QuickLaTeX.com \[ \frac{1}{4} \cdot 400 = 100\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d93bfd498cc335bf3fbab61bfb58f841_l3.png)
Welche der vier Rechnungen haben das gleiche Ergebnis?
- 40% von 200€
- 40% von 400€
- 20% von 400€
- 20% von 200€
Lösung:
Antwort: 1. und 3. liefern das gleiche Ergebnis.
Wie groß ist der Grundwert, wenn 40% 100€ entsprechen?
Lösung:
- Was ist gegeben? Du weißt den Prozentsatz
 und den Prozentwert
und den Prozentwert  .
. - Was ist gesucht? Gesucht ist der Grundwert
 .
. - Setze den Prozentsatz und Prozentwert in die richtige Formel ein.
- Rechenweg:
![Rendered by QuickLaTeX.com \[ G = \frac{W}{p\,\%} = \frac{\SI{100}{\euro}}{\SI{40}{\percent}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-89db1b74624f165e204a5e4916b42e90_l3.png)
- Wandle die Prozentzahl um:
 .
. ![Rendered by QuickLaTeX.com \[ G = \frac{\SI{100}{\euro}}{\frac{4}{10}} = \frac{\SI{100}{\euro} \cdot 10}{4} = \SI{250}{\euro} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e036a677ead252b69792bfa5be46f946_l3.png)
Alternativer Rechenweg mit dem Dreisatz :
- Schreibe auf, was du weißt:

- Dividiere beide Seiten durch 40:

- Multipliziere beide Seiten mit 100:

Antwort: 100% entsprechen 250€. Der Grundwert muss also 250€ betragen.
Wie groß ist der Grundwert, wenn 30% 600g entspricht?
Lösung:
- Was ist gegeben? Du weißt den Prozentsatz
 und den Prozentwert
und den Prozentwert  .
. - Was ist gesucht? Der Grundwert
 ist gesucht.
ist gesucht. - Setze den Prozentsatz und Prozentwert in die richtige Formel ein.
- Rechenweg:
![Rendered by QuickLaTeX.com \[ G = \frac{W}{p\,\%} = \frac{\SI{600}{\gram}}{\SI{30}{\percent}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ac108fbeccafd3f064156df5d48280be_l3.png)
- Wandle die Prozentzahl um:
 .
.
![Rendered by QuickLaTeX.com \[ G = \frac{\SI{600}{\gram}}{\frac{3}{10}} = \frac{\SI{600}{\gram}\cdot 10}{3} = \SI{2000}{\gram} = \SI{2}{\kilo\gram} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-7a2e102fc30bad1d78e65c9e92c08a4d_l3.png)
Wie groß ist der Grundwert, wenn 120% 600€ entsprechen?
Lösung:
- Was ist gegeben? Du weißt den Prozentsatz
 und den Prozentwert
und den Prozentwert  .
. - Was ist gesucht? Der Grundwert
 ist gesucht.
ist gesucht. - Setze den Prozentsatz und den Prozentwert in die Formel ein. Lass dich nicht durch den hohen Prozentsatz irritieren. Die Rechnungen mit Prozentsätzen größer als 100% funktionieren wie alle anderen Aufgaben.
- Rechenweg:
![Rendered by QuickLaTeX.com \[ G = \frac{W}{p\,\%} = \frac{\SI{600}{\euro}}{\SI{120}{\percent}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9a4d23901bcd094facdd0001ad8cc08b_l3.png)
- Wandle die Prozentzahl um:
 .
.
![Rendered by QuickLaTeX.com \[ G = \frac{ \SI{600}{\euro} }{ \frac{6}{5} } = \frac{ \SI{600}{\euro}\cdot 5 }{6} = \SI{500}{\euro} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f2ce7b71c315dc2315ec021a5f6727f4_l3.png)
Wieviel sind 15% von 40?
Lösung:
- Was ist gegeben? Du weißt den Prozentsatz
 und den Grundwert
und den Grundwert  .
. - Was ist gesucht? Gesucht ist der Prozentwert
 .
. - Setze deine Angabe in die Prozentformel ein.
- Rechenweg:
![Rendered by QuickLaTeX.com \[ W = G\cdot p\,\% = 40 \cdot \SI{15}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-974fdc2a5b6abdd38fd559e40731357d_l3.png)
- Wandle um:
 .
.
![Rendered by QuickLaTeX.com \[ W = 40 \cdot \SI{15}{\percent} = 40 \cdot \frac{15}{100} = \frac{4\cdot 15}{10} = 6 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3208674621fc406b3e64ff7f4157a899_l3.png)
Wie viel sind 20% von 50€?
Lösung:
- Was ist gegeben? Du weißt den Prozentsatz
 und den Grundwert
und den Grundwert  .
. - Was ist gesucht? Gesucht ist der Prozentwert
 .
. - Setze die Angaben in die Prozentformel ein.
- Rechenweg:
![Rendered by QuickLaTeX.com \[ W = G\cdot p\,\% = \SI{50}{\euro}\cdot\SI{20}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ebdf68105a25ff56fb097919a35bb0ec_l3.png)
- Wandle um:
 .
.
![Rendered by QuickLaTeX.com \[ W=\SI{50}{\euro}\cdot\SI{20}{\percent} = \SI{50}{\euro}\cdot\frac{1}{5} = \SI{10}{\euro} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-28d52e92f09b9f4324514917d00d53ee_l3.png)
Wieviel Prozent sind 45 von 150?
Lösungsweg:
- Was ist gegeben? Du weißt den Prozentwert
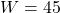 und den Grundwert
und den Grundwert  .
. - Was ist gesucht? Gesucht wird der Prozentsatz
 .
. - Setze die Angaben in die Prozentsatzformel ein:

- Wandle um:
![Rendered by QuickLaTeX.com \[ \frac{1}{4} = \frac{3\cdot 10}{10\cdot 10} = \frac{30}{100} = \SI{30}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-2ead6bd4f120873378a97b8766927a8e_l3.png)
Wie viel Prozent sind 42g von 200g?
Lösungsweg:
- Was ist gegeben? Gegeben ist der Prozentwert
 und der Grundwert
und der Grundwert  .
. - Was ist gesucht? Gesucht wird der Prozentsatz
 .
. - Setze deine Angaben in die Prozentsatzformel ein:

- Kürze den Bruch mit 2:
![Rendered by QuickLaTeX.com \[ p\,\% = \frac{\SI{42}{\gram}}{\SI{200}{g}} = \frac{\SI{2}{\gram}\cdot 21}{\SI{2}{\gram}\cdot 100} = \frac{21}{100} = \SI{21}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9fedf0cc098c22c9aab23a8e9ec0c520_l3.png)
Stell dir vor, in deiner Klasse sind 25 Schüler und 20% sind im Musikverein. Welche Rechnung ist richtig?

Antwort:  ist die richtige Rechnung.
ist die richtige Rechnung.
Lösung:
- 20% ist genau ein Fünftel. Ein Fünftel kannst Du auch als Bruch (
 ) oder Dezimalzahl (0,2) schreiben.
) oder Dezimalzahl (0,2) schreiben. - Um den Anteil von etwas Ganzem (25) auszurechnen, multiplizierst du die 20% und 25.
- Somit ist
 die einzige richtige Rechnung.
die einzige richtige Rechnung. - Wenn du die falschen Antworten korrigierst, bekommst du diese Rechenwege:
![Rendered by QuickLaTeX.com \[ \begin{array}{l l l l} \text{1.} & 0,2 \cdot 25 &=& 5 \\ \text{2.} & \SI{20}{\percent} \cdot 25 &=& 5 \\ \text{3.} & \frac{1}{5} \cdot 25 &=& 5 \\ \end{array} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9326e86b66d18b6b3a9283673bc56016_l3.png)
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Textaufgaben
Häufig musst du auch bei Textaufgaben prozentrechnen.
Robert hat viele Urlaubsfotos geschossen. Jedes Foto braucht 2MB auf seiner Speicherkarte. Er kann insgesamt 1GB auf ihr speichern. Wie viel Prozent seines Speichers ist belegt, wenn er 100 Fotos geschossen hat? (Tipp:  )
)
Lösung:
- Wenn 1 Foto 2MB Platz braucht, dann sind 100 Fotos 200MB groß.
- Was ist also gegeben? Du weißt den Grundwert
 und den Prozentwert
und den Prozentwert  .
. - Was ist gesucht? Der Prozentsatz
 ist gesucht.
ist gesucht. - Setze beides in die Prozentsatzformel ein:
![Rendered by QuickLaTeX.com \[ p\,\% = \frac{W}{G} = \frac{\SI{200}{MB}}{\SI{1000}{MB}} = \frac{20}{100} = \SI{20}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-56680f4944924fccdfda0551fe173c9a_l3.png)
Antwort: Die 100 Urlaubfotos belegen 20% der Speicherkarte.
Auf Roberts Speicherkarte (1GB) sind noch 80% frei für Urlaubsfotos. Wie viele Fotos kann er noch schießen, wenn jedes Foto 4MB braucht? (Tipp:  )
)
Lösung:
- Was ist gegeben? Der Grundwert
 und der Prozentsatz
und der Prozentsatz  sind gegeben.
sind gegeben. - Was ist gesucht? Der Prozentwert
 ist gesucht.
ist gesucht. - Setze beides in die Prozentwertformel ein:
![Rendered by QuickLaTeX.com \[ W = G \cdot p\,\% = \SI{1000}{MB} \cdot \SI{80}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-26e60768e14c543763389dc9d98709f4_l3.png)
- Wandle die Prozentzahl um:
 .
.
![Rendered by QuickLaTeX.com \[ W = \SI{1000}{MB} \cdot \frac{8}{10} = \frac{ \SI{1000}{MB} \cdot 8}{10} = \SI{800}{MB} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c39598b4ae83d74c52ae5807806fa6b6_l3.png)
- Du weißt jetzt, dass 800MB Speicher noch frei ist. Wie viele Urlaubsfotos passen also in 800MB? Du weißt, dass ein Foto 4MB groß ist. Teile also 800MB durch die 4MB!
![Rendered by QuickLaTeX.com \[ \frac{\SI{800}{MB}}{\SI{4}{MB}} = 200 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-296fc628bdd6682108b13ed602eb437c_l3.png)
Antwort: Robert kann noch 200 weitere Fotos schießen.
Stell dir vor du besuchst deine Familie und fährst von Regensburg nach Köln. Ihr fahrt mit 60 Litern im Tank los. Nach 3 Stunden fahrt sind nur noch 15% des Benzins übrig. Wie viel Liter Benzin sind noch im Tank?
Lösung:
- Was ist gegeben? Der Grundwert
 und der Prozentsatz
und der Prozentsatz  ist gegeben. Die 3 Stunden helfen dir nicht bei der Lösung der Aufgabe.
ist gegeben. Die 3 Stunden helfen dir nicht bei der Lösung der Aufgabe. - Was ist gesucht? Gesucht wird der Prozentwert
 .
. - Setze also Grundwert und Prozentsatz in die Prozentsatzformel ein.
![Rendered by QuickLaTeX.com \[ W = G \cdot p\,\% = \SI{60}{\liter}\cdot\SI{15}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-1cec07ae781a03520bec3284a94b1b7b_l3.png)
- Wandle um:

![Rendered by QuickLaTeX.com \[ W = \SI{60}{\liter}\cdot\SI{15}{\percent} = \frac{\SI{60}{\liter}\cdot 15}{100} = 9{\liter} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-3090f7ecec7cad6f617d6e0002a8ee84_l3.png)
Antwort: Es sind noch 9 Liter im Tank.
Aufgabe 9
Wie viel Zucker solltest du maximal essen?
Lösung:
- Was ist gegeben? Du kennst den Prozentwert
 und den Prozentsatz
und den Prozentsatz  .
. - Was ist gesucht? Gesucht wird der Grundwert
 .
. - Setze also in die Grundwertformel ein.
![Rendered by QuickLaTeX.com \[ G = \frac{W}{p\,\%} = \frac{\SI{1.9}{\gram}}{\SI{2}{\percent}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-99b11fc58df69c9230ee25197e5ce14b_l3.png)
- Wandle um:
 .
.
![Rendered by QuickLaTeX.com \[ G = \frac{\SI{1.9}{\gram}}{\SI{2}{\percent}} = \frac{\SI{1.9}{\gram}}{\frac{2}{100}} = \frac{\SI{1.9}{\gram}\cdot 100}{2} = \SI{95}{\gram} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-710e2e0d64b7ecbeb7308fb550037005_l3.png)
9 Schüler aus deiner Klasse spielen in der Schulband. Das sind ungefähr 32% der ganzen Klasse. Schätze die Größe deiner Klasse ab!
Lösung:
- Was ist gegeben? Gegeben ist der Prozentwert
 und der Prozentsatz
und der Prozentsatz  .
. - Was ist gesucht? Gesucht wird der Grundwert

- Setze also in die Grundwertformel ein.
![Rendered by QuickLaTeX.com \[ G = \frac{W}{p\,\%} \approx \frac{9}{\SI{30}{\percent}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4ac51228215d81f3e9e71d00494c5200_l3.png)
- Wandle um:
 .
.
![Rendered by QuickLaTeX.com \[ G \approx \frac{9}{\SI{32}{\percent}} = \frac{9}{\frac{32}{100}} = \frac{9\cdot 100}{32} = 28.125 \approx 28 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-cb25a44d09928d99a891bd93a3494665_l3.png)
Antwort: Die Klasse besteht aus 28 Schülern.
Beim Überprüfen von 320 Fahrrädern stellt die Polizei fest, dass 25% keine Katzenaugen haben. Von diesen 25% wird  aus dem Verkehr gezogen. Wie viele Fahrräder dürfen nicht mehr gefahren werden?
aus dem Verkehr gezogen. Wie viele Fahrräder dürfen nicht mehr gefahren werden?
Lösung:
- Rechne zuerst aus wie viele Fahrräder mangelhaft sind.
- Was ist gegeben? Gegeben ist der Grundwert
 und der Prozentsatz
und der Prozentsatz  .
. - Was ist gesucht? Gesucht wird der Prozentwert
 .
. - Setze deine Angaben in die Prozentwertformel ein.
![Rendered by QuickLaTeX.com \[ W = G\cdotp\,\% = 320\cdot\SI{25}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-8a42022a8ebc65584ec3b98079c2bd43_l3.png)
- Wandle um:
 .
.
![Rendered by QuickLaTeX.com \[ W = 320\cdot\SI{25}{\percent} = 320 \cdot \frac{1}{4} = 80 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-d117b2aa7e55c2c50d01292575c9a691_l3.png)
- 80 Fahrräder haben also keine Katzenaugen.
 davon dürfen nicht mehr gefahren werden. Wie viele sind das?
davon dürfen nicht mehr gefahren werden. Wie viele sind das? - Was ist gegeben? Gegeben ist der Grundwert
 und der Prozentsatz
und der Prozentsatz  .
. - Hinweis: Obwohl der Prozentsatz nicht in Prozent geschrieben ist, kannst du alle Formeln normal benutzen.
- Was ist gesucht? Gesucht ist der Prozentwert
 .
. - Setze deine Angaben in die Prozentwertformel ein.
![Rendered by QuickLaTeX.com \[ W = G\cdot p\,\% = 80 \cdot \frac{1}{10} = 8 \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0174ca00a431132e7bd0cf5e069d215e_l3.png)
Antwort: Von den 320 überprüften Fahrrädern dürfen 8 nicht mehr benutzt werden.
Wie viel Prozent sind 78 Gramm von 2600 Gramm?
Lösung:
- Was ist gegeben? Gegeben ist der Grundwert
 und der Prozentwert
und der Prozentwert  .
. - Was ist gesucht? Gesucht ist der Prozentsatz
 .
. - Setze Deine Angaben in die Prozentsatzformel ein.
![Rendered by QuickLaTeX.com \[ p\,\% = \frac{W}{G} = \frac{\SI{78}{\gram}}{\SI{2600}{\gram}} = \frac{78}{2600} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-90d2c77eb51c255bf45eb03a466f686f_l3.png)
- Die Aufgabe sieht schwerer aus als sie eigentlich ist. 78 ist ein Vielfaches von 26. Du kannst den Bruch also kürzen.
![Rendered by QuickLaTeX.com \[ p\,\% = \frac{78}{2600} = \frac{\cancel{26}\cdot 3}{\cancel{26}\cdot 100} = \frac{3}{100} = \SI{3}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-967f43d4e779112952bd1c6dac66db41_l3.png)
Antwort: 78 Gramm sind 3% von 2600 Gramm.
Prozentuale Veränderung berechnen
Versuche dich auch an etwas kniffligeren Textaufgaben, damit die Prozentrechnung dir schnell von der Hand geht!
Du möchtest ein Auto kaufen, dass normalerweise für 26.800€ verkauft wird. Für deine Sonderausstattung kommen noch mal 1.200€ dazu. Zum Glück gibt es aber einen Rabatt von 14%. Wie viel Prozent vom eigentlichen Grundpreis musst Du bezahlen?
Lösung:
- Löse die Aufgabe am besten in zwei Schritten. Beantworte als erstes: Wie viel musst Du für das Auto bezahlen?
- Ohne Rabatt kostet das Auto:
 .
. - Was ist gegeben? Gegeben ist der Grundwert
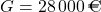 und der Prozentsatz
und der Prozentsatz  .
. - Was ist gesucht? Gesucht wird der Prozentwert
 .
. - Setze deine Angaben in die Prozentwertformel ein.
![Rendered by QuickLaTeX.com \[ W = G\cdot p\,\% = \SI{28000}{\euro} \cdot \SI{14}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-972f798615d261a1f9cd5a1426087142_l3.png)
- Wandle um:

![Rendered by QuickLaTeX.com \[ W = \SI{28000}{\euro} \cdot \SI{14}{\percent} = \frac{ \SI{28000}{\euro} \cdot 14 }{100} = \SI{3920}{\euro} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-425ab0e7105adead56fe4162124fea01_l3.png)
- Subtrahiere den Rabatt vom ursprünglichen Kaufpreis.
![Rendered by QuickLaTeX.com \[ \SI{28000}{\euro} - \SI{3920}{\euro} = \SI{24080}{\euro} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-a4b67feb1a1044601b8c7a3f403715ad_l3.png)
- Du musst also 24080€ für das Auto bezahlen. Wie viel Prozent sind das vom Grundpreis?
- Was ist gegeben? Der übliche Kaufpreis ist der Grundwert
 . Der Prozentwert
. Der Prozentwert  ist auch gegeben.
ist auch gegeben. - Was ist gesucht? Der Prozentsatz
 ist gesucht.
ist gesucht. - Setze die Angaben in die Prozentsatzformel ein.
![Rendered by QuickLaTeX.com \[ p\,\% = \frac{W}{G} = \frac{ \SI{24080}{\euro} }{ \SI{26800}{\euro} } \approx 0,90 = \SI{90}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c7265edfd7a6fcb4d3553acc52d4e158_l3.png)
Antwort: Du bezahlst mit Sonderausstattung und Rabatt 90% des üblichen Kaufpreises.
Beide Angebote werben mit einem Preisnachlass von 1€, aber welches bietet prozentual mehr Rabatt?
Lösung:
- Rechne den Rabatt für beide Angebote getrennt aus und vergleiche sie am Ende. Fange mit dem ersten Angebot an.
- Was ist gegeben? Gegeben ist der Grundwert
 und der Prozentwert
und der Prozentwert  .
. - Was ist gesucht? Gesucht ist der Prozentsatz
 .
. - Setze deine Angaben in die Prozentsatzformel ein.
![Rendered by QuickLaTeX.com \[ p\,\% = \frac{W}{G} = \frac{\SI{13.99}{\euro}}{\SI{14.99}{\euro}} \approx 0,93 = \SI{93}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-f45a55a063d3a51c302b7fa27855b4f0_l3.png)
- Beim ersten Angebot zahlst du nur 93% des eigentlichen Preises. Wie sieht es mit dem zweiten Angebot aus?
- Was ist gegeben? Gegeben ist wieder der Grundwert
 und der Prozentwert
und der Prozentwert  .
. - Was ist gesucht? Gesucht wird erneut der Prozentsatz
 .
. - Setze die Preise in die Prozentsatzformel ein.
![Rendered by QuickLaTeX.com \[ p\,\% = \frac{W}{G} = \frac{ \SI{11.99}{\euro} }{ \SI{12.99}{\euro} } \approx 0,92 = \SI{92}{\percent} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-399dbeb17a124ca51e4c3aa348c62247_l3.png)
- Beim zweiten Angebot musst du nur 92% bezahlen. Es ist also prozentual günstiger.
Antwort: Das zweite Angebot ist prozentual günstiger, weil du nur 92% des eigentlichen Preises bezahlst. Für das andere Angebot sind es 93%.
Zinsrechnung
Super, jetzt bist du fit in der Prozentrechnung! Aber kennst du dich auch mit dem kleinen Bruder, der Zinsrechnung aus? Wenn du dir nicht ganz sicher bist, schau dir am besten noch unser Video zur Zinsrechnung an!






