Einheitskreis
In diesem Beitrag beschäftigen wir uns mit dem Einheitskreis. Wir zeigen dir, wie er definiert ist und wie du ihn verwenden kannst, um Winkelfunktionen zu veranschaulichen.
Du schaust gerne Lernvideos? Perfekt! Denn auch zum Einheitskreis haben wir ein eigenes Video für dich!
Inhaltsübersicht
Einheitskreis einfach erklärt
Der Begriff Einheitskreis enthält die zwei Bestandteile „Einheit“ und „Kreis“. Mit „Kreis“ wird seine geometrische Form gemeint, das heißt, es handelt sich um einen Kreis. Die Bezeichnung „Einheit“ bezieht sich auf folgende Beobachtung: Nimmst du irgendeinen Punkt entlang des Kreisrandes, dann wird dieser Punkt einen Abstand zum Mittelpunkt des Kreises von exakt 1 besitzen. Sehr oft ist der Mittelpunkt des Einheitskreises mit dem Ursprung eines Koordinatensystems identisch.
Mit Hilfe des Einheitskreises kannst du die Definition der Winkelfunktionen Sinus, Cosinus und Tangens auf alle Winkel erweitern. Zusätzlich erlaubt er dir die charakteristischen Kurven dieser Winkelfunktionen zu konstruieren.
Definition Einheitskreis
Allgemein ist der Rand eines Kreises um den Ursprung mit Radius  definiert als die Sammlung aller Punkte
definiert als die Sammlung aller Punkte  , die zum Ursprung den Abstand
, die zum Ursprung den Abstand  besitzen. Wie bestimmst du den Abstand eines Punktes
besitzen. Wie bestimmst du den Abstand eines Punktes  mit den Koordinaten
mit den Koordinaten  und
und  zum Ursprung? Du verwendest dafür den Satz des Pythagoras. Wenn wir den Abstand des Punktes
zum Ursprung? Du verwendest dafür den Satz des Pythagoras. Wenn wir den Abstand des Punktes  zum Ursprung mit
zum Ursprung mit  bezeichnen, dann gilt
bezeichnen, dann gilt

und da sich der Punkt auf dem Kreisrand befinden soll, gilt
 .
.
Damit erhalten wir die Gleichung
 .
.
Jeder Punkt, der sich auf dem Kreisrand befindet, wird diese Gleichung erfüllen. Für den Einheitskreis ist  . Somit können wir den Einheitskreis folgendermaßen definieren
. Somit können wir den Einheitskreis folgendermaßen definieren
Der Einheitskreis um den Ursprung ist die Menge aller Punkte, die zum Ursprung den Abstand 1 besitzen, das heißt
Einheitskreis =  ,
,
wobei  und
und  die Koordinaten des Punktes
die Koordinaten des Punktes  sind.
sind.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Einheitskreis Sinus und Cosinus
In diesem Abschnitt zeigen wir dir, wie du mit Hilfe vom Einheitskreis den Sinus und Cosinus für alle Winkel definieren kannst.
Wir können die  – und
– und  -Koordinate eines Punktes
-Koordinate eines Punktes  auf dem Einheitskreis geometrisch folgendermaßen bestimmen: Wir zeichnen ein rechtwinkliges Dreieck, sodass der Punkt eine Ecke des Dreiecks und der Abstand zum Ursprung die Hypotenuse ist. Die Länge der Hypotenuse kennen wir. Sie beträgt genau 1, da alle Punkte auf dem Kreis per Definition den Abstand 1 zum Ursprung haben. Bilden wir das Verhältnis zwischen Gegenkathete und Hypotenuse, so erhalten wir
auf dem Einheitskreis geometrisch folgendermaßen bestimmen: Wir zeichnen ein rechtwinkliges Dreieck, sodass der Punkt eine Ecke des Dreiecks und der Abstand zum Ursprung die Hypotenuse ist. Die Länge der Hypotenuse kennen wir. Sie beträgt genau 1, da alle Punkte auf dem Kreis per Definition den Abstand 1 zum Ursprung haben. Bilden wir das Verhältnis zwischen Gegenkathete und Hypotenuse, so erhalten wir

und für das Verhältnis Ankathete zu Hypotenuse
 .
.
Das heißt, dass der Sinus gerade die  -Koordinate und der Cosinus die
-Koordinate und der Cosinus die  -Koordinate des Punktes
-Koordinate des Punktes  ist.
ist.
Einheitskreis Tangens
Der Tangens
lässt sich auf ähnliche Weise auf alle Winkel erweitern. Für den Tangens müssen wir aber das Dreieck im Einheitskreis solange skalieren, bis die Ankathete zum Winkel  gleich 1 ist (die Winkel im Dreieck bleiben unverändert). Der Punkt
gleich 1 ist (die Winkel im Dreieck bleiben unverändert). Der Punkt  mit den Koordinaten
mit den Koordinaten  wird dabei zum Punkt
wird dabei zum Punkt  mit den Koordinaten
mit den Koordinaten  . Bilden wir für dieses skalierte Dreieck das Verhältnis zwischen Gegenkathete und Ankathete, so erhalten wir
. Bilden wir für dieses skalierte Dreieck das Verhältnis zwischen Gegenkathete und Ankathete, so erhalten wir
 .
.
Das heißt, dass der Tangens gerade die  -Koordinate des Punktes
-Koordinate des Punktes  ist. Beachte, wie die Gegenkathete beim skalierten Dreieck gerade tangential zum Einheitskreis ist. Daher kommt auch die Bezeichnung Tangens. Das folgende Bild illustriert die beschriebene Konstruktion, wobei das skalierte Dreieck nicht schraffiert dargestellt ist.
ist. Beachte, wie die Gegenkathete beim skalierten Dreieck gerade tangential zum Einheitskreis ist. Daher kommt auch die Bezeichnung Tangens. Das folgende Bild illustriert die beschriebene Konstruktion, wobei das skalierte Dreieck nicht schraffiert dargestellt ist.
Einheitskreis und Trigonometrische Funktionen
Mit dem Einheitskreis kannst du auch die charakteristischen Kurven der Winkelfunktion konstruieren. Diese Kurven sind die Bilder der sogenannten trigonometrischen Funktionen .
Um zu sehen, wie sich der Wert des Sinus und Cosinus als Funktion des Winkels  verhält, lassen wir den Winkel
verhält, lassen wir den Winkel  einmal um den Einheitskreis laufen und notieren uns für jeden
einmal um den Einheitskreis laufen und notieren uns für jeden  -Wert die
-Wert die  – und
– und  -Koordinate des Punktes. Für den Sinus sieht die Konstruktion folgendermaßen aus.
-Koordinate des Punktes. Für den Sinus sieht die Konstruktion folgendermaßen aus.
Der Cosinus verhält sich ähnlich. Er beginnt aber nicht bei 0 wie der Sinus, sondern bei 1. Das veranschaulicht das folgende Bild.
Tabelle wichtiger Werte
Für bestimmte Winkel sind die Werte des Sinus, Cosinus und Tangens einfache Ausdrücke. Die folgende Tabelle enthält ein paar dieser Winkel und die dazugehörigen Werte.
Winkel 
|
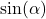 |
 |
 |
| 0° | 0 | 1 | 0 |
| 30° |  |
 |
 |
| 45° |  |
 |
1 |
| 60° |  |
 |
 |
| 90° | 1 | 0 | n. d. |
| 180° | 0 | -1 | 0 |
| 270° | -1 | 0 | n. d. |
Die Bezeichnung „n. d.“ ist die Abkürzung für „nicht definiert“, da sich für diese Winkel die Tangenskurve einer senkrechten Asymptote nähert.
Gradmaß und Bogenmaß
Bei der Berechnung der Werte für die Winkelfunktionen musst du unbedingt darauf achten, ob die Winkel im Gradmaß oder im Bogenmaß angegeben sind. Im Fall der Tabelle von vorhin waren die Winkel alle im Gradmaß angegeben. Entsprechend musst du auch deinen Taschenrechner auf „DEG“ einstellen, wenn du die Werte nachrechnen möchtest.
Die Umrechnung zwischen Gradmaß und Bogenmaß basiert auf folgender Beziehung
 °.
°.
Wenn du beispielsweise wissen möchtest, wie ein Winkel von  ° in Bogenmaß lautet, dann rechnest du
° in Bogenmaß lautet, dann rechnest du
 .
.
Auf deinem Taschenrechner findest du das Bogenmaß unter der Abkürzung „RAD“.
Einheitskreis — häufigste Fragen
(ausklappen)
Einheitskreis — häufigste Fragen
(ausklappen)-
Was genau ist ein Einheitskreis im Koordinatensystem?Ein Einheitskreis im Koordinatensystem ist ein Kreis, dessen Mittelpunkt im Ursprung liegt und dessen Radius genau 1 beträgt. Das bedeutet: Jeder Punkt auf dem Kreisrand hat vom Ursprung aus den Abstand 1. So lassen sich Winkel und Winkelfunktionen geometrisch veranschaulichen.
-
Wie erkenne ich an der Gleichung x² plus y² gleich 1 den Einheitskreis?An der Gleichung
 erkennst du den Einheitskreis, weil sie genau alle Punkte beschreibt, deren Abstand zum Ursprung 1 ist. Der Abstand erfüllt nach dem Satz des Pythagoras
erkennst du den Einheitskreis, weil sie genau alle Punkte beschreibt, deren Abstand zum Ursprung 1 ist. Der Abstand erfüllt nach dem Satz des Pythagoras  und bei Radius 1 gilt dann
und bei Radius 1 gilt dann
 .
.
-
Wie lese ich am Einheitskreis den Sinus als y-Koordinate ab?Am Einheitskreis ist
 genau die y-Koordinate des Punktes auf dem Kreisrand, der zum Winkel
genau die y-Koordinate des Punktes auf dem Kreisrand, der zum Winkel  gehört. Das liegt daran, dass im rechtwinkligen Dreieck die Hypotenuse 1 ist und damit
gehört. Das liegt daran, dass im rechtwinkligen Dreieck die Hypotenuse 1 ist und damit  . Zum Beispiel gilt bei
. Zum Beispiel gilt bei
 :
:  , weil die y-Koordinate 0 ist.
, weil die y-Koordinate 0 ist.
-
Wie lese ich am Einheitskreis den Cosinus als x-Koordinate ab?Am Einheitskreis ist
 genau die x-Koordinate des Punktes auf dem Kreisrand, der zum Winkel
genau die x-Koordinate des Punktes auf dem Kreisrand, der zum Winkel  gehört. Im rechtwinkligen Dreieck ist die Hypotenuse 1, daher gilt
gehört. Im rechtwinkligen Dreieck ist die Hypotenuse 1, daher gilt  . Zum Beispiel gilt bei
. Zum Beispiel gilt bei
 :
:  , weil die x-Koordinate -1 ist.
, weil die x-Koordinate -1 ist.
-
Warum ist der Tangens bei 90 Grad nicht definiert?Der Tangens ist bei
 nicht definiert, weil sich die Tangenskurve dort einer senkrechten Asymptote nähert. Deshalb steht in Wertetabellen bei
nicht definiert, weil sich die Tangenskurve dort einer senkrechten Asymptote nähert. Deshalb steht in Wertetabellen bei  oft „n. d.“ für „nicht definiert“. Das gleiche gilt auch bei
oft „n. d.“ für „nicht definiert“. Das gleiche gilt auch bei  , wo ebenfalls „n. d.“ angegeben wird.
, wo ebenfalls „n. d.“ angegeben wird.
Beispiel: Gradmaß und Bogenmaß umrechnen
Nehmen wir an, dass du einen Winkel von 60° gegeben. Wie lautet dieser Winkel im Bogenmaß? Dazu rechnest du
 .
.
Umgekehrt, wenn du einen Winkel von  im Bogenmaß gegeben hast und du den dazugehörigen Winkel in Gradmaß bestimmen möchtest, dann rechnest du
im Bogenmaß gegeben hast und du den dazugehörigen Winkel in Gradmaß bestimmen möchtest, dann rechnest du
 .
.
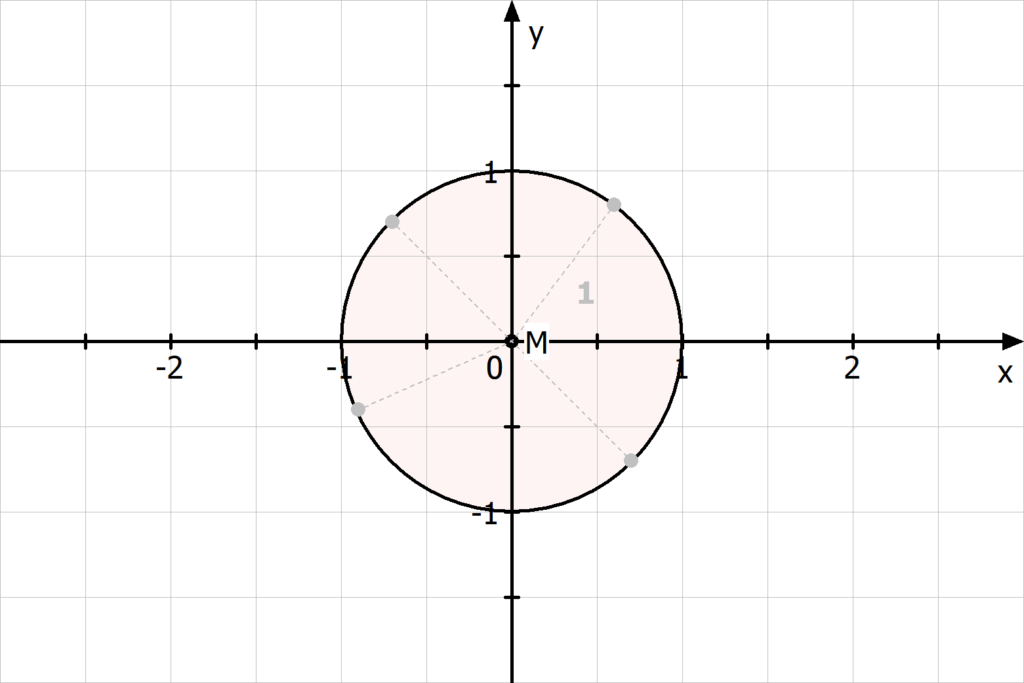


 , da die
, da die  , da die
, da die 

 , da die
, da die 

