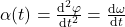Winkelgeschwindigkeit und Winkelbeschleunigung
Die Winkelgeschwindigkeit und Winkelbeschleunigung sind Größen, die sehr oft in der klassischen Mechanik bei Rotationsbewegungen verwendet werden. Mit ihnen lassen sich Rotationsbewegungen, wie zum Beispiel die Rotation der Erde, beschreiben.
Um die gesamte Thematik für dich noch anschaulicher darzustellen, haben wir ein Video für dich erstellt. Hier findest du alles Wichtige graphisch aufbereitet.
Inhaltsübersicht
Winkelgeschwindigkeit
Die Winkelgeschwindigkeit ist eine vektorielle Größe und beschreibt in der Physik die zeitliche Änderung eines Winkels. Sie zeigt in die Richtung der Drehachse und wird mit einem kleinen Omega als Formelzeichen dargestellt. Da mit der Winkelgeschwindigkeit oft Rotationen beschrieben werden, wird sie deshalb auch als Rotationsgeschwindigkeit oder Drehgeschwindigkeit bezeichnet.
Winkelgeschwindigkeit Formel
In diesem Abschnitt wird die Formel der Winkelgeschwindigkeit vorgestellt. Die Winkelgeschwindigkeit  beschreibt die zeitliche Änderung eines Rotationswinkels
beschreibt die zeitliche Änderung eines Rotationswinkels  , sodass der Betrag der Winkelgeschwindigkeit durch die zeitliche Ableitung des Rotationswinkels dargestellt werden kann
, sodass der Betrag der Winkelgeschwindigkeit durch die zeitliche Ableitung des Rotationswinkels dargestellt werden kann

Mit dieser Formel der Winkelgeschwindigkeit, kann diese also einfach durch Ableiten des Winkels nach der Zeit berechnet werden. Geht man von einer konstanten Winkelgeschwindigkeit aus, dann ist diese gerade das Verhältnis einer Umdrehung mit dem Winkel  zur Umlaufzeit T. Die Formel für die Winkelgeschwindigkeit ausgedrückt mit der Umlaufzeit T ist dann gegeben durch
zur Umlaufzeit T. Die Formel für die Winkelgeschwindigkeit ausgedrückt mit der Umlaufzeit T ist dann gegeben durch

Wobei T die Zeit ist, die für eine Umdrehung benötigt wird.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Winkelgeschwindigkeit Einheit
Die Winkelgeschwindigkeit ist der Quotient aus der Änderung des Rotationswinkels  , gemessen im Bogenmaß, und der benötigten Zeit t, gemessen in Sekunden. Für die SI-Einheit der Winkelgeschwindigkeit erhält man somit
, gemessen im Bogenmaß, und der benötigten Zeit t, gemessen in Sekunden. Für die SI-Einheit der Winkelgeschwindigkeit erhält man somit  . Hierbei ist rad der Radiant, welcher die Einheit des Bogenmaßes darstellt. Das Bogenmaß wird häufig zur Winkelmessung bei Rotationen eingesetzt, da man mit ihm oft einfacher rechnen kann, als mit dem Gradmaß. Es beschreibt den Winkel als Kreisbogen auf einem Einheitskreis. Eine Umdrehung von 360° auf einem Einheitskreis entspricht dann gerade dem Bogenmaß . Damit lassen sich das Bogenmaß und das Gradmaß einfach ineinander umrechnen. Hat man einen Winkel
. Hierbei ist rad der Radiant, welcher die Einheit des Bogenmaßes darstellt. Das Bogenmaß wird häufig zur Winkelmessung bei Rotationen eingesetzt, da man mit ihm oft einfacher rechnen kann, als mit dem Gradmaß. Es beschreibt den Winkel als Kreisbogen auf einem Einheitskreis. Eine Umdrehung von 360° auf einem Einheitskreis entspricht dann gerade dem Bogenmaß . Damit lassen sich das Bogenmaß und das Gradmaß einfach ineinander umrechnen. Hat man einen Winkel  [Grad] in Grad gegeben, dann kann man diesen mit dem Bogenmaß x [rad] in der Einheit Radiant, wie folgt ausdrücken
[Grad] in Grad gegeben, dann kann man diesen mit dem Bogenmaß x [rad] in der Einheit Radiant, wie folgt ausdrücken
![Rendered by QuickLaTeX.com x[rad] = \frac{\pi}{180}\Psi [Grad]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-151e29861b6c20676b9d46fdbbd0ad91_l3.png)
Umgekehrt kann man natürlich auch aus einem Winkel, der in der Einheit Radiant gegeben ist, den Winkel in der Einheit Grad berechnen
![Rendered by QuickLaTeX.com \Psi [Grad] = \frac {180}{\pi}x[rad]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e85eeb77b5d9c4f0dd96662845b41e4e_l3.png)
Berechnung mittels Bahngeschwindigkeit
Betrachtet man zum Beispiel eine Scheibe, die sich mit konstanter Geschwindigkeit dreht, so bewegen sich Gegenstände auf der Scheibe umso schneller, desto weiter sie vom Rotationsmittelpunkt entfernt sind. Diese Geschwindigkeit v kann man mit Hilfe der Winkelgeschwindigkeit  berechnen, mit
berechnen, mit

v wird in diesem Zusammenhang auch als Bahngeschwindigkeit bezeichnet, da sie die Geschwindigkeit der Körper beschreibt, die sich auf einer Kreisbahn um den Mittelpunkt bewegen. Wie schon erwähnt, ist die Bahngeschwindigkeit der Gegenstände auf der Scheibe umso größer, je weiter sie vom Rotationsmittelpunkt entfernt sind. Die Winkelgeschwindigkeit  hingegen ist für alle Gegenstände auf der Scheibe gleich, da sie alle in derselben Zeit T eine Rotation von
hingegen ist für alle Gegenstände auf der Scheibe gleich, da sie alle in derselben Zeit T eine Rotation von  zurücklegen. Die Winkelgeschwindigkeit kannst du bei gegebener Bahngeschwindigkeit berechnen mit
zurücklegen. Die Winkelgeschwindigkeit kannst du bei gegebener Bahngeschwindigkeit berechnen mit

Berechnung in Polarkoordinaten
Als nächstes Beispiel werden wir die Winkelgeschwindigkeit einer Kreisbewegung in Polarkoordinaten darstellen und zeigen, wie man die Winkelgeschwindigkeit berechnet. Dies bietet sich immer dann an, wenn eine Bewegung in einer festen Ebene erfolgt. Als Ausgangspunkt seien die Basisvektoren in ebenen Polarkoordinaten gegeben durch


Hierbei beschreibt  den Winkel zwischen der x-Achse und des Basisvektors
den Winkel zwischen der x-Achse und des Basisvektors  . Der Basisvektor
. Der Basisvektor  ist immer tangential zu Bahntangente und
ist immer tangential zu Bahntangente und  zeigt in die radiale Richtung. Der Ortsvektor sei gegeben durch
zeigt in die radiale Richtung. Der Ortsvektor sei gegeben durch

Über das Differential dr lässt sich damit die Geschwindigkeit  ermitteln
ermitteln

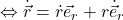

da  , denn
, denn  und
und  .
.  ist dabei die Änderung des Winkels
ist dabei die Änderung des Winkels  pro Zeiteinheit, sodass dies gerade die Winkelgeschwindigkeit
pro Zeiteinheit, sodass dies gerade die Winkelgeschwindigkeit  darstellt, also
darstellt, also  . Berechnet man den Geschwindigkeitsbetrag, so erhält man dasselbe Ergebnis wie im vorherigen Beispiel
. Berechnet man den Geschwindigkeitsbetrag, so erhält man dasselbe Ergebnis wie im vorherigen Beispiel

Im Folgenden gehen wir darauf ein, wie man die Kreisgeschwindigkeit in drei Dimensionen berechnen kann. Betrachtet man eine Bewegung in drei Dimensionen, so zeigt eine Komponente des Geschwindigkeitsvektors  in Richtung des Radius und eine Komponente senkrecht dazu
in Richtung des Radius und eine Komponente senkrecht dazu  , also tangential zur Kreisbewegung.
, also tangential zur Kreisbewegung.
Die Rotationsachse ist dabei wie im zweidimensionalen Fall senkrecht zur aufgespannten Ebene von  und
und  . Somit gilt, dass
. Somit gilt, dass

Damit lässt sich die Winkelgeschwindigkeit in Zylinder– oder Kugelkoordinaten einfach berechnen.
Berechnung in Zylinderkoordinaten
Betrachten wir zuerst die Winkelgeschwindigkeit in Zylinderkoordinaten. Dabei gehen wir von folgendem Ortsvektor aus

womit sich die folgenden Basisvektoren ergeben.



Die Geschwindigkeit  erhält man nun durch Differentiation des Ortsvektors
erhält man nun durch Differentiation des Ortsvektors  nach
nach  .
.

Setzt man den Ortsvektor  und die Geschwindigkeit
und die Geschwindigkeit  in die Formel für die Winkelgeschwindigkeit ein, und drückt anschließend die Winkelgeschwindigkeit mit den Basisvektoren aus, liefert dies
in die Formel für die Winkelgeschwindigkeit ein, und drückt anschließend die Winkelgeschwindigkeit mit den Basisvektoren aus, liefert dies


Stellt man diese Formel nach  um, dann lässt sich die Winkelgeschwindigkeit berechnen mit
um, dann lässt sich die Winkelgeschwindigkeit berechnen mit

Berechnung in Kugelkoordinaten
Als letztes Beispiel wird gezeigt, wie man die Winkelgeschwindigkeit in Kugelkoordinaten berechnen kann. Dabei gehen wir von folgendem Ortsvektor aus

Hieraus ergeben sich die Basisvektoren



Berechnet man analog zum vorherigen Beispiel die Geschwindigkeit  durch Differentiation von
durch Differentiation von  nach t und setzt das Ergebnis in die Formel für die Winkelgeschwindigkeit ein, so erhält man
nach t und setzt das Ergebnis in die Formel für die Winkelgeschwindigkeit ein, so erhält man

Mit dieser Formel kann man die Winkelgeschwindigkeit in Kugelkoordinaten berechnen.
Winkelgeschwindigkeit Frequenz
Die Winkelgeschwindigkeit kann auch in Abhängigkeit der Frequenz ausgedrückt werden. Die Frequenz f ist der Kehrwert der Periodendauer T.
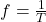
Hiermit ergibt sich

Winkelgeschwindigkeit Erde
Im Folgenden wird als Beispiel die Winkelgeschwindigkeit der Erde berechnet. Dabei gehen wir annäherungsweise davon aus, dass die Erde sich in 24 Stunden einmal um die eigene Achse dreht. Es werden sämtliche Effekte vernachlässigt, die zu Schwankungen der Umdrehungsdauer führen. Mit der oberen Formel erhält man damit:

Die Bahngeschwindigkeit eines bestimmten Objektes auf der Erde hängt im Gegensatz zur Winkelgeschwindigkeit von dem Breitengrad ab, an dem es sich befindet. Direkt über dem Nord– oder Südpol ist die Bahngeschwindigkeit gleich null, da die Rotationsachse der Erde direkt durch den Nord- und Südpol verläuft. Im Gegensatz dazu hat ein Objekt auf der Erde eine maximale Bahngeschwindigkeit, wenn es sich auf dem Äquator befindet. Mit der oberen Formel lässt sich die Bahngeschwindigkeit eines Objektes am Äquator wie folgt ermitteln.

wobei r = 6378km den Erdradius repräsentiert. Dieser ist der Abstand vom Äquator zur Rotationsachse.
Fun-Fact: Die Rotation der Erde führt unter anderem dazu, dass man am Äquator etwas leichter ist, als an den Polen.
Winkelbeschleunigung
Die Winkelbeschleunigung beschreibt die zeitliche Änderung der Winkelgeschwindigkeit. Dies bedeutet, dass die Winkelbeschleunigung die Ableitung der Winkelgeschwindigkeit nach der Zeit ist.
Mathematisch kann dieser Zusammenhang zwischen Winkelgeschwindigkeit  und Winkelbeschleunigung
und Winkelbeschleunigung  durch die zeitliche Ableitung ausgedrückt werden.
durch die zeitliche Ableitung ausgedrückt werden.

Die Winkelbeschleunigung darf nicht mit der Tangentialbeschleunigung verwechselt werden, welche die Ableitung der Bahngeschwindigkeit darstellt,

wobei r den Abstand zur Rotationsachse repräsentiert. Betrachtet man eine Kreisbewegung, so zeigt die Winkelbeschleunigung in die tangentiale Richtung. Zusätzlich zur Winkelbeschleunigung, wirkt auf den Körper auch noch die sogenannte Radialbeschleunigung , oder auch Zentripetalbeschleunigung genannt. Die Radialbeschleunigung und Winkelbeschleunigung sind senkrecht zueinander. Da bei einer Kreisbewegung die Geschwindigkeit immer tangential zur Kreisbewegung ist, ändert die Geschwindigkeit ständig ihre Richtung. Die Geschwindigkeit wird andauernd zum Kreismittelpunkt hin beschleunigt. Diese Beschleunigung wird Radialbeschleunigung genannt. Die Gesamtbeschleunigung bei einer Kreisbewegung kann dann durch die Summe der Winkelbeschleunigung und der Radialbeschleunigung ausgedrückt werden.
Winkelbeschleunigung Formel
Die Winkelbeschleunigung 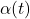 lässt sich mathematisch wie folgt ausdrücken.
lässt sich mathematisch wie folgt ausdrücken.

Wenn  konstant ist, also wenn der Quotient aus der Änderung der Kreisgeschwindigkeit und der Änderung der Zeit konstant ist, dann spricht man von einer Kreisbewegung mit konstanter Beschleunigung.
konstant ist, also wenn der Quotient aus der Änderung der Kreisgeschwindigkeit und der Änderung der Zeit konstant ist, dann spricht man von einer Kreisbewegung mit konstanter Beschleunigung.
Winkelbeschleunigung Einheit
Die Einheit der Winkelbeschleunigung ergibt sich aus der letztgenannten Formel zu

da die Winkelbeschleunigung das Verhältnis der Änderung der Drehgeschwindigkeit und der Änderung der Zeit beschreibt.
Winkelbeschleunigung berechnen
Zwischen der Winkelbeschleunigung, dem Drehmoment M und dem Trägheitsmoment I besteht eine enge Beziehung, welche folgende Formel zum Ausdruck bringt

Möchtest du mehr über das Drehmoment wissen, dann schau unseren extra Beitrag Drehmoment
dazu an. Nach der Eulersche’n Gleichung, entspricht die Änderung des Drehimpulses gerade dem Moment  , so dass man folgenden Zusammenhang zwischen Drehimpuls und Winkelbeschleunigung erhält
, so dass man folgenden Zusammenhang zwischen Drehimpuls und Winkelbeschleunigung erhält

Interessiert dich, was der Drehimpuls physikalisch beschreibt und wie du ihn berechnen kannst, dann schau unseren extra Beitrag Drehimpuls dazu an.
Winkel, Winkelgeschwindigkeit und Winkelbeschleunigung
Im Folgenden wird noch einmal übersichtlich der Zusammenhang zwischen dem Rotationswinkel  , der Winkelgeschwindigkeit
, der Winkelgeschwindigkeit  und der Winkelbeschleunigung
und der Winkelbeschleunigung  dargestellt. Geht man von einem Rotationswinkel
dargestellt. Geht man von einem Rotationswinkel  aus, dann kann daraus die Winkelgeschwindigkeit berechnet werden, indem man die Winkelgeschwindigkeit nach der Zeit ableitet
aus, dann kann daraus die Winkelgeschwindigkeit berechnet werden, indem man die Winkelgeschwindigkeit nach der Zeit ableitet

Durch weiteres einmaliges Ableiten der Drehgeschwindigkeit nach der Zeit, erhält man dann die Winkelbeschleunigung 

Dies ist gleichbedeutend mit der zweimaligen zeitlichen Ableitung des Rotationswinkels  . Die Winkelbeschleunigung
. Die Winkelbeschleunigung  lässt sich also auch in Abhängigkeit des Rotationswinkels
lässt sich also auch in Abhängigkeit des Rotationswinkels  wie folgt ausdrücken
wie folgt ausdrücken