Halb- und Volladdierer
Du möchtest wissen, was Halb- und Volladdierer sind? Im Folgenden zeigen wir dir, wie du Binärzahlen mit Hilfe von Halb- und Volladdierern digital addieren kannst.
Inhaltsübersicht
Halbaddierer Definition, Schaltsymbol, Wahrheitstabelle und Umsetzung
Halb- und Volladdierer sind digitale Schaltnetze, die dazu dienen, einstellige Binärzahlen zu addieren. Schauen wir uns zunächst einmal den Halbaddierer an.
Der Halbaddierer wird auf Englisch auch „half adder“ genannt und kann zwei einstellige Binärzahlen addieren. Er hat daher zwei Eingänge und auch zwei Ausgänge. Der Output S liefert dabei die Summe und der Output C den Übertrag. Das C stammt von der englischen Bezeichnung „carry“. Den Übertrag kennst du eventuell noch aus der händischen Addition von Binärzahlen. Betrachten wir nun zunächst das Schaltsymbol und die zugehörige Wahrheitstabelle für den Halbaddierer:
Diese entspricht den folgenden Gleichungen:
Damit sind wir schon fast fertig mit den Halbaddierern! Schauen wir uns noch die Umsetzung an. Die einfachste Darstellung eines Halbaddierers erfolgt durch ein Und-Gatter und ein XOR-Gatter. Die Schaltung sieht so aus:
Der Halbaddierer kann allerdings auch anders dargestellt werden, beispielsweise durch Und-Gatter oder durch Oder-Gatter. Es gibt hier relativ viele Möglichkeiten für die Konstruktion, die Herangehensweise bleibt dabei natürlich immer die gleiche.
Volladdierer Schaltung und Wahrheitstabelle
Wenden wir uns nun dem Volladdierer zu. Dieser kann drei einstellige Binärzahlen addieren. Dementsprechend besitzt er drei Inputs 
, 
und 
. Die Ausgänge 
und 
bleiben gleich. Werfen wir nun wieder einen Blick auf das Schaltsymbol und die Wahrheitstabelle für die Volladdierer. FA steht dabei für den englischen Begriff „full adder“.
Wir haben links die möglichen Kombinationen unserer drei Inputs und rechts die Summe S und den Übertrag. Wie bei dem Halbaddierer können wir auch das wieder durch boolesche Algebra darstellen. Wir schreiben die Begriffe mit einem Minterm, also mit einer 1 als Output aus der Tabelle und erhalten folgende zwei Gleichungen:
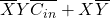
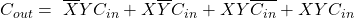
Wir können die Begriffe noch vereinfachen und erhalten:
Der Volladdierer kann am einfachsten durch zwei Halbaddierer und ein Oder-Gatter dargestellt werden.
Da wir den Halbaddierer schon durch verschiedene Gatter darstellen können, gibt es auch hier für den Volladdierer wieder weitere Darstellungsmöglichkeiten.
Nun kennst du beide Addiererarten, aber wo werden sie eigentlich verwendet? Beide sind ein wichtiger Bestandteil von Addiernetzen. Diese werden in Prozessoren eingesetzt. Insbesondere Halbaddierer sind häufig in Mikroprozessoren zu finden. Nun hast du Halb- und Volladdierer kennengelernt, weißt, wie sie funktionieren und wofür sie eingesetzt werden.