Zweierkomplement
Der Computer kann Daten nur im Binärsystem, also nur mit Nullen und Einsen, verarbeiten. Das Problem auf das man schnell stößt sind die negative Zahlen, da es im Binärsystem kein Vorzeichen im herkömmlichen Sinne gibt. Abhilfe schafft hier das Zweierkomplement, das wir dir in diesem Video behandeln werden.
Wir haben zu diesem Thema auch ein Video erstellt, damit du die Inhalte noch einfacher verstehen kannst.
Inhaltsübersicht
Zweierkomplement einfach erklärt
Das Zweierkomplement ist eine Darstellungsform für binäre Zahlen, mit dem man positive und negative Zahlen abbildet. Es ist die am häufigsten verwendete Form in der Digitaltechnik, da damit direkte Rechenoperationen, wie Addition oder Multiplikation, ohne Umrechnungen möglich sind.
Zweierkomplementdarstellung
Im Binärsystem gibt es kein Vorzeichen so wie wir es kennen. Falls du nicht genau weist was das Binärsystem ist, schaue dir unbedingt unser Video zu Zahlensystemen an! Ein weiteres Beispiel, wie man einen Binärcode aufstellt, findest du auch in unserem Video zur Hamming-Distanz , welches du dir ebenfalls gerne ansehen kannst.
Um nun negative und positive Zahlen im Binärcode abzubilden, benutzt man ein Bit als Vorzeichen. Dabei gibt es verschiedene Varianten. Beim Least Significant Bit (LSB) Verfahren wird das Bit 0, also das am weitesten rechts stehende Bit, für das Vorzeichen genutzt. Damit kann man aber trotzdem nicht ohne weitere Umformungen rechnen. Deshalb wird im Zweierkomplement das Most Significant Bit (MSB), also das Bit welches am weitesten links steht, als Vorzeichenbit genutzt. Dabei steht eine 0 an der MSB-Stelle für positive Zahlen. Im Umkehrschluss dient dementsprechend eine 1 als negatives Vorzeichen.
Im 2er Komplement kann man einen Wertebereich von

darstellen. In dieser Formel steht  für die Anzahl der Bits. Für 4 Bits kannst du also die Zahlen
für die Anzahl der Bits. Für 4 Bits kannst du also die Zahlen
 bis
bis 
abbilden. Um Verwechslungen zu vermeiden zeigen die tiefgestellten Symbole an, welche Darstellungsform genutzt wird. Die Tiefgestellte 2 steht für das Binärsystem, und die tiefgestellte 10 für das Dezimalsystem.
Wie du diese Werte berechnen kannst, zeigen wir dir im nächsten Kapitel.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Zweierkomplement bilden
Eine Binärzahl wird ins 2er Komplement gewandelt, indem die einzelnen Bits erst invertiert und dann eine 1 hinzuaddiert wird. Schau dir folgendes Beispiel an. Du willst die Zahl  im Zweierkomplement darstellen. Als erstes wandelst du den Betrag der Zahl, in den Binärcode um
im Zweierkomplement darstellen. Als erstes wandelst du den Betrag der Zahl, in den Binärcode um
 .
.
Im nächsten Schritt invertierst du die einzelnen Stellen der Binären Zahl. Invertieren bedeutet, dass du jede 0 mit einer 1 und jede 1 mit einer 0 vertauscht. Für unsere Zahl folgt dementsprechend
 .
.
Zum Schluss muss noch eine 1 addiert werden
 ,
,
und du hast erfolgreich das Zweierkomplement gebildet.
Zweierkomplement umwandeln
Vor der Umwandlung zum Dezimalsystem musst du zuerst das MSB ansehen. Ist diese eine 0, kannst du die Zahl direkt umrechnen. Ist das MSB jedoch eine 1 musst du den Binärcode invertieren, danach eine eins dazu addieren und zum Schluss erst ins Dezimalsystem umwandeln. Als Beispiel führen wir diese Überlegungen an  durch. Du erkennst eine führende 1, weshalb du zuerst die einzelnen Bits invertierst
durch. Du erkennst eine führende 1, weshalb du zuerst die einzelnen Bits invertierst
 ,
,
und daraufhin eine 1 addierst.
 .
.
Jetzt musst du dir das negative Vorzeichen noch dazu denken und du erhältst die anfangs gegebene  . Die Umwandlung ins Dezimalsystem kannst du aber auch mit folgendem Trick schneller durchführen. Dazu rechnest du die Binärzahl wie gewohnt in das Dezimalsystem um, jedoch subtrahierst du das MSB, anstatt es zu addieren.
. Die Umwandlung ins Dezimalsystem kannst du aber auch mit folgendem Trick schneller durchführen. Dazu rechnest du die Binärzahl wie gewohnt in das Dezimalsystem um, jedoch subtrahierst du das MSB, anstatt es zu addieren.
Du rechnest also

und erhältst so auch die  .
.
Zweierkomplement Addition
Wichtige Grundlagen zum Rechnen im Binärcode findest du in unserem Video zur Booleschen Algebra
. Zur Addition zweier Binärzahlen kannst du die sogenannte Schulrechenmethode benutzen. Das bedeutet, dass du die zu addierenden Zahlen untereinander schreibst, und die Bits nacheinander zusammenzählst, angefangen beim LSB. Das erkennst du am besten an einem Beispiel. Dazu wollen wir die einfache Rechnung  im Binärcode durchführen. Dazu rechnest du erst beide Dezimalzahlen in binäre Zahlen um und addierst sie dann wie beschrieben.
im Binärcode durchführen. Dazu rechnest du erst beide Dezimalzahlen in binäre Zahlen um und addierst sie dann wie beschrieben.
Du siehst bei dieser Beispielrechnung, dass wenn man zwei Einsen in einer Spalte addiert eine 0 entsteht und eine 1 als Übertrag in die nächste Spalte wandert. Wandelst du zum Schluss das Ergebnis  in das Dezimalsystem erhältst du auch die zuvor genannte
in das Dezimalsystem erhältst du auch die zuvor genannte  .
.
Zweierkomplement Subtraktion
Die Subtraktion basiert auf dem selben Prinzip wie die Addition. Willst du also  rechnen, musst du die Dezimalzahlen wieder in das Zweierkomplement umwandeln. Du kannst dir die Subtraktion wie
rechnen, musst du die Dezimalzahlen wieder in das Zweierkomplement umwandeln. Du kannst dir die Subtraktion wie 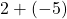 vorstellen, also eine Addition mit einer negativen Zahl.
vorstellen, also eine Addition mit einer negativen Zahl.
Führst du die Addition mit der Schulrechenmethode wieder durch, erhältst du als Ergebnis  . Wandelst du dieses in das Dezimalsystem um, findest du das Ergebnis
. Wandelst du dieses in das Dezimalsystem um, findest du das Ergebnis  .
.
Zweierkomplement Multiplikation
Die Multiplikation im Zweierkomplement wird durch Erweiterung, Verschiebung und Addition bewerkstelligt. Schauen wir uns dazu das Beispiel  . Zuerst bildest du wie gewohnt das Zweierkomplement. Danach führst du die Vorzeichenerweiterung durch. Du erweiterst die Binäre Zahl links vom MSB mit dem Wert des MSB so oft, bis sich die Bits insgesamt verdoppeln. Das verändert den Wert der Zahl nicht. Aus
. Zuerst bildest du wie gewohnt das Zweierkomplement. Danach führst du die Vorzeichenerweiterung durch. Du erweiterst die Binäre Zahl links vom MSB mit dem Wert des MSB so oft, bis sich die Bits insgesamt verdoppeln. Das verändert den Wert der Zahl nicht. Aus  wird also
wird also  . Die Multiplikation funktioniert nun genauso wie die Multiplikation mit der Schulrechenmethode.
. Die Multiplikation funktioniert nun genauso wie die Multiplikation mit der Schulrechenmethode.
Als erstes multiplizierst du den ersten Faktor ( ) mit dem rechten Bit vom zweiten Faktor (
) mit dem rechten Bit vom zweiten Faktor ( ), also mit 1. Das Zwischenergebnis schreibst du ohne Verschiebung darunter. Im nächsten Schritt multiplizierst du den ersten Faktor mit dem zweiten Bit von rechts vom zweiten Faktor, nun also mit 0. Das Ergebnis schreibst du jetzt um ein Bit nach links verschoben unter das erste Zwischenergebnis auf. Das führt man so lange durch, bis man den ersten Faktor letztendlich mit dem MSB multipliziert hat. Danach musst du alle Zwischenergebnisse addieren. Zum Schluss zählst du die Anzahl der Bits der Faktoren und alle Bits des Ergebnisses die über diese Anzahl gehen streichst du einfach. Somit erhältst du in unserem Beispiel das Ergebnis
), also mit 1. Das Zwischenergebnis schreibst du ohne Verschiebung darunter. Im nächsten Schritt multiplizierst du den ersten Faktor mit dem zweiten Bit von rechts vom zweiten Faktor, nun also mit 0. Das Ergebnis schreibst du jetzt um ein Bit nach links verschoben unter das erste Zwischenergebnis auf. Das führt man so lange durch, bis man den ersten Faktor letztendlich mit dem MSB multipliziert hat. Danach musst du alle Zwischenergebnisse addieren. Zum Schluss zählst du die Anzahl der Bits der Faktoren und alle Bits des Ergebnisses die über diese Anzahl gehen streichst du einfach. Somit erhältst du in unserem Beispiel das Ergebnis  .
.
Zweierkomplement Rechnen
Zur Vertiefung kannst du dir folgende Beispielaufgabe anschauen. Rechne  binär aus und gebe das Ergebnis in Dezimalform an.
binär aus und gebe das Ergebnis in Dezimalform an.
Zuerst addierst du die Binärzahlen in der Klammer zusammen und erhältst
 .
.
Wenn du nun die Multiplikation durchführst bekommst du
 .
.
Diese Zahl kannst du in Dezimalform umwandeln und somit findest du das Ergebnis
 .
.
Einerkomplement bilden
Das Einerkomplement ist ebenfalls eine Möglichkeit negative Ziffern darzustellen. Man bildet, es indem man die Bits einer Binärzahl negiert. Als Beispiel kannst du das Einerkomplement von  bilden. Dafür musst du zuerst den Betrag der Zahl in Binärcode umwandeln. Du erhältst also
bilden. Dafür musst du zuerst den Betrag der Zahl in Binärcode umwandeln. Du erhältst also
 .
.
Im nächsten Schritt musst du nur noch alle Bits invertieren

und du erhältst das Einerkomplement der Zahl  . Das MSB zeigt dir, genau wie beim Zweierkomplement wieder das Vorzeichen an. Eine 1 am MSB steht also ebenfalls für eine negative Zahl, eine 0 für eine positive.
. Das MSB zeigt dir, genau wie beim Zweierkomplement wieder das Vorzeichen an. Eine 1 am MSB steht also ebenfalls für eine negative Zahl, eine 0 für eine positive.
Einerkomplement Zweierkomplement
Der Nachteil vom Einerkomplement ist, dass es in dieser Zahlendarstellung zwei Werte für die Null gibt, einmal  und einmal
und einmal  . Sozusagen eine positive und eine negative Null. Um dem entgegenzuwirken wird zum Einerkomplement eine Eins addiert. So entsteht, wie bereits behandelt, das Zweierkomplement. Der Vorteil vom 2er Komplement ist dementsprechend die Eindeutigkeit der Null.
. Sozusagen eine positive und eine negative Null. Um dem entgegenzuwirken wird zum Einerkomplement eine Eins addiert. So entsteht, wie bereits behandelt, das Zweierkomplement. Der Vorteil vom 2er Komplement ist dementsprechend die Eindeutigkeit der Null.



