De Morgansche Regeln
Du möchtest wissen, was die De Morgansche Regeln sind? Im Folgenden zeigen wir dir, was es genauer damit auf sich hat und wie man sie in der Digitaltechnik anwendet.
Inhaltsübersicht
Die erste De Morgansche Regel
Die De Morganschen Regeln oder auch De Morgansche Gesetze sind zwei elementare Gesetze der Aussagenlogik und der Mengenlehre. Benannt wurden sie nach dem bekannten Mathematiker Augustus De Morgan.
Die De Morganschen Gesetze werden vor allem für das Entwerfen von digitalen Schaltkreisen benutzt, um unnötige Bauteile einzusparen oder zu ersetzen. Die erste Morgansche Regel lautet:
Wie du hier sehen kannst, gibt es verschiedene Möglichkeiten das Gesetz darzustellen. Alle Darstellungsweisen bedeuten genau dasselbe. Der horizontale Strich über oder vor der Funktion steht für die Nicht-Funktion. Das Malzeichen und das Dach stehen für die logische Und-Funktion und das umgedrehte Dach und das plus stehen für die logische Oder-Funktion.
Das zweite Morgansches Gesetz
Schauen wir uns nun das zweite De Morgansche Gesetz an:
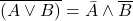
Auch hier gibt es wieder verschiedene Möglichkeiten das Gesetz abzubilden.
Grundsätzlich können die Morgan´schen Regeln für beliebig viele Elemente erweitert werden. So könnten wir unsere Gleichungen beispielsweise um die Variablen C oder D erweitern.
Wahrheitstabelle: De Morgan Beweis
Ob die Morgan´schen Regel wirklich immer zutreffen, kann mit Hilfe einer Wahrheitstabelle bewiesen werden. Schauen wir uns das ganze doch mal mit zwei Variablen an. In den ersten vier Spalten habe wir alle möglichen Kombinationen der Variablen A und B und ihre Inversen. Um das erste De Morgansche Gesetz zu beweisen, teilen wir es in die Gleichungen rechts und links des ist-gleich Zeichens auf. Wir schauen uns nun die Ergebnisse für beide Gleichungen an. Für die linke Seite nehmen wir A und B mal und drehen dann das Ergebnis um. Für die rechte Seite addieren wir nicht A und nicht B. Hier musst du die Rechenregeln der booleschen Algebra berücksichtigen.
Wie du sehen kannst, stimmen die Spalten links und rechts des ist-gleich Zeichens überein. Somit haben wir das 1. De Morgan´sche Gesetz bewiesen.
Beweis 2. De Morgan Regel
Jetzt können wir dies auch für das 2. De Morgan´sche Gesetz versuchen. Wir gehen analog vor. Versuch es doch mal ohne Hilfe! Kommst du auch bei beiden Spalten auf 1 0 0 0? Natürlich lassen sich diese Gesetze auch für mehrere Variablen problemlos mit der Wahrheitstabelle überprüfen. Dies wird mit zunehmender Variablenzahl allerdings immer aufwändiger, deshalb verzichten wir hier auf die Durchführung.
Nun weißt du, wie die De Morganschen Gesetze lauten und hast bewiesen, dass sie auch wirklich anwendbar sind.