Bruchrechnen
Du fragst dich, wie du mit Brüchen rechnest? Hier im Beitrag und im Video erklären wir dir es!
Inhaltsübersicht
Bruchrechnen — Grundlagen
Mit einem Bruch kannst du Zahlen angeben, die zwischen 1, 2, 3, 4, … usw. liegen. Ein Bruch zeigt dir nämlich an, wie viele Teile von einem Ganzen du hast.
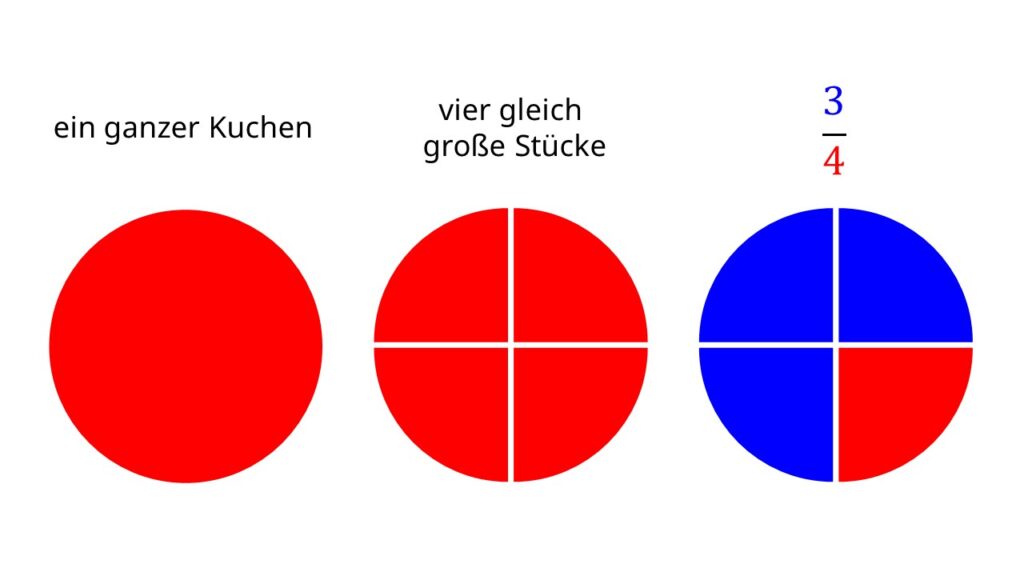
Stell dir zum Beispiel vor, du teilst einen Kuchen in 4 gleich große Stücke und isst dann 3 Stücke. Wenn du jetzt angeben willst, wie viel du von dem Kuchen du schon gegessen hast, kannst du das als Bruch schreiben.
Dafür schreibst du die gegessenen Stücke über den Strich. Die Anzahl, in wie viele Stücke du den Kuchen geteilt hast, schreibst du unter den Bruchstrich.

Bruchrechnen — Zähler und Nenner
Ein Bruch besteht also aus zwei Zahlen: Die Zahl unter dem Bruchstrich heißt Nenner. Der Nenner sagt dir, in wie viele Teile das Ganze insgesamt geteilt wurde. In unserem Beispiel wurde der Kuchen in 4 Teile geteilt. Der Nenner ist hier also die 4.

Die Zahl über dem Bruchstrich nennst du Zähler. Er sagt dir, wie viele Teile des Ganzen gemeint sind. Du hast 3 Stücke von den 4 Kuchenstücken gegessen. Der Zähler in unserem Beispiel ist also die 3.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Brüche kürzen und erweitern
Wenn du Brüche kürzt oder erweiterst, kannst du sie einfacher machen und so leichter mit ihnen rechnen oder sie vergleichen.
-
Brüche kürzen:
Wenn du den Zähler und den Nenner durch dieselbe Zahl teilst, heißt das kürzen.
![Rendered by QuickLaTeX.com \[\frac{\textcolor{blue}4}{\textcolor{red}6} = \frac{\textcolor{blue}4:2}{\textcolor{red}6:2}=\frac{\textcolor{blue}2}{\textcolor{red}3}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-0e00c40da69a99ca3b0c85866683ad98_l3.png)
-
Brüche erweitern:
Beim Erweitern machst du das Gegenteil. Du multiplizierst beide Zahlen mit derselben Zahl.
![Rendered by QuickLaTeX.com \[\frac{\textcolor{blue}1}{\textcolor{red}4} = \frac{\textcolor{blue}1\cdot 3}{\textcolor{red}4\cdot 3}=\frac{\textcolor{blue}3}{\textcolor{red}{12}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-89d4ec0777075337910d9bb1f635e3e6_l3.png)
Bruchrechnen — Plus rechnen (Addieren)
Stell dir vor, du hast  und ein Freund hat
und ein Freund hat  von einem Kuchen. Wenn ihr wissen wollt, wie viel Kuchen ihr zusammen habt, müsst ihr die Brüche addieren.
von einem Kuchen. Wenn ihr wissen wollt, wie viel Kuchen ihr zusammen habt, müsst ihr die Brüche addieren.
Bei deinen Brüchen sind die Zahlen unter dem Bruchstrich gleich. Deshalb rechnest du nur die Zähler plus und lässt den Nenner einfach stehen:
![Rendered by QuickLaTeX.com \[\frac{1}{4}+\frac{2}{4}=\frac{1+2}{4}=\frac{3}{4}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-dd19a2c50fb746be07aa8f520cfef430_l3.png)
Zusammen habt ihr also einen  Kuchen.
Kuchen.
Stell dir nun vor, dein Freund hat nur  von seinem Kuchen. Jetzt haben die beiden Brüche unterschiedliche Zahlen unter dem Bruchstrich.
von seinem Kuchen. Jetzt haben die beiden Brüche unterschiedliche Zahlen unter dem Bruchstrich.
Wenn du die  und die
und die  addieren willst, musst als Erstes dafür sorgen, dass die Nenner gleich sind. Dazu erweiterst du die Brüche:
addieren willst, musst als Erstes dafür sorgen, dass die Nenner gleich sind. Dazu erweiterst du die Brüche:
![Rendered by QuickLaTeX.com \[\frac{1}{4} = \frac{1\cdot 3}{4\cdot 3}=\frac{3}{12}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-c866bbc35d8c9ef1ff56f99454a78c08_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{6} = \frac{1\cdot 2}{6\cdot 2}=\frac{2}{12}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-e072c47b647eca3a235828bb04794e4e_l3.png)
Dann kannst du wieder die beiden Zähler plus rechnen und den neuen Nenner 12 einfach stehen lassen.
![Rendered by QuickLaTeX.com \[\frac{3}{12}+\frac{2}{12}=\frac{3+2}{12}=\frac{5}{12}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ffddb3e197ee34a9ef2b44c3a2543a8d_l3.png)
- Brüche auf den gleichen Nenner bringen.
- Zähler addieren und Nenner stehen lassen.
Bruchrechnen — Minus rechnen (Subtrahieren)
Das Subtrahieren von Brüchen
funktioniert sehr ähnlich: Zum Beispiel willst du  rechnen. Bei diesen Brüchen sind die Zahlen unter dem Bruchstrich gleich. Deshalb rechnest du nur die Zähler minus und lässt den Nenner einfach stehen:
rechnen. Bei diesen Brüchen sind die Zahlen unter dem Bruchstrich gleich. Deshalb rechnest du nur die Zähler minus und lässt den Nenner einfach stehen:
![Rendered by QuickLaTeX.com \[\frac{3}{4} - \frac{1}{4} = \frac{3 - 1}{4} = \frac{2}{4}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-4e660ece3903cd98ca3b55163340dbd5_l3.png)
Jetzt stell dir vor, die beiden Brüche haben unterschiedliche Zahlen unten, z. B. 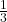 und
und  . Hier musst du wieder zuerst die Nenner gleich machen, damit du sie subtrahieren kannst. Dazu erweiterst du sie.
. Hier musst du wieder zuerst die Nenner gleich machen, damit du sie subtrahieren kannst. Dazu erweiterst du sie.
![Rendered by QuickLaTeX.com \[\frac{1}{3} = \frac{1 \cdot 5}{3 \cdot 5} = \frac{5}{15}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-48bb8a209bee1633c17e09708e21578d_l3.png)
![Rendered by QuickLaTeX.com \[\frac{1}{5} = \frac{1 \cdot 3}{5 \cdot 3} = \frac{3}{15}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-ad4d237fbf5fcbac9554ab63e3418417_l3.png)
Jetzt kannst du die Zähler minus rechnen und den Nenner stehen lassen.
![Rendered by QuickLaTeX.com \[\frac{5}{15} - \frac{3}{15} = \frac{5 - 3}{15} = \frac{2}{15}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-60942baec75bd88aec2bb8ae0e4dc2e2_l3.png)
- Brüche auf den gleichen Nenner bringen.
- Zähler subtrahieren und Nenner stehen lassen.
Bruchrechnen — Mal rechnen (Multiplizieren)
Zum Brüche multiplizieren, rechnest du Zähler mal Zähler (Zahlen oben) und Nenner mal Nenner (Zahlen unten). Schauen wir uns das an einem Beispiel an:
![Rendered by QuickLaTeX.com \[\frac{2}{3}\cdot \frac{3}{5}=\frac{2\cdot 3}{3 \cdot 5}=\frac{6}{15}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-092bc56a3b08894e6685da8de8a646d5_l3.png)
Beim Malrechnen ist es also egal, ob die Nenner gleich oder unterschiedlich sind.
Gut zu wissen: Oft kannst du Ergebnisse kürzen, um einen kleineren Bruch zu schreiben. Hierfür teilst du Zähler und Nenner durch ihren größten gemeinsamen Teiler.
In unserem Beispiel ist der größte gemeinsame Teiler 3. Du kannst  also zu
also zu  kürzen.
kürzen.
- Zähler mal Zähler rechnen.
- Nenner mal Nenner rechnen.
Bruchrechnen — Geteilt rechnen (Dividieren)
Wenn du Brüche dividieren möchtest, vertauschst du Zähler und Nenner des zweiten Bruchs. Dann rechnest du ihn mal den ersten:
![Rendered by QuickLaTeX.com \[\frac{2}{3}:\frac{4}{5}=\frac{2}{3}\cdot\frac{5}{4}=\frac{2\cdot 5}{3\cdot 4}=\frac{10}{12}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-b06c0483d9e39641aafcd5549079ffd1_l3.png)
Schon gewusst? Ein Bruch, bei dem der Zähler und Nenner vertauscht werden, heißt Kehrbruch.
- Kehrbruch des zweiten Bruches bestimmen.
- Brüche multiplizieren.
Rechnen mit Brüchen — Zusammenfassung
Hier haben wir dir nochmal zusammengefasst, wie du mit Brüchen rechnest.
Brüche addieren:
- Rechne die beiden Zähler (Zahlen oben) zusammen
- Wenn die Nenner (Zahlen unten) gleich sind, lass sie stehen
- Wenn unten im Nenner verschiedene Zahlen stehen, musst du sie auf den kleinsten gemeinsamen Nenner bringen, bevor du die Zähler (Zahlen oben) zusammenrechnest.
Brüche subtrahieren:
- Ziehe die Zähler (Zahlen oben) voneinander ab
- Wenn die Nenner (Zahlen unten) gleich sind, lass sie stehen
- Wenn unten im Nenner verschiedene Zahlen stehen, musst du sie auf den kleinsten gemeinsamen Nenner bringen, bevor du die Zähler (Zahlen oben) minus rechnest.
Brüche multiplizieren:
- Nimm Zähler mal Zähler (Zahlen oben) und Nenner mal Nenner (Zahlen unten)
- Es ist egal, ob unten im Nenner dieselbe Zahl steht oder nicht
Brüche dividieren:
- Nimm den ersten Bruch mal den Kehrbruch des zweiten Bruchs
- Der Kehrbruch ist ein umgekehrter Bruch, bei dem du die untere und obere Zahl vertauschst.
- Es ist egal, ob unten im Nenner dieselbe Zahl steht oder nicht
Bruchrechnen — häufigste Fragen
(ausklappen)
Bruchrechnen — häufigste Fragen
(ausklappen)-
Wie rechne ich Bruch aus?Brüche subtrahierst du, indem du Zähler minus Zähler rechnest. Für die Addition von Brüchen rechnest du Zähler plus Zähler. Bei der Multiplikation nimmst du Zähler mal Zähler und Nenner mal Nenner. Eine Division wird zur Multiplikation, indem du Zähler und Nenner beim zweiten Bruch vertauschst.
-
Was sind Brüche in der 6. Klasse?Ein Bruch sind zwei Zahlen, die über bzw. unter einem Strich stehen — dem sogenannten Bruchstrich. Die obere Zahl nennst du Zähler und die untere Zahl Nenner.
-
Wie geht die Bruchrechnung?Um zwei Brüche zu addieren, müssen beide Nenner gleich sein und dann rechnest du die beiden Zähler plus. Dasselbe gilt für die Subtraktion. Beim Multiplizieren rechnest du Zähler mal Zähler und Nenner mal Nenner.
Bruchrechnen Regeln
Jetzt weißt du, wie du mit Brüchen rechnest. Wenn du alle Bruchrechnen Regeln nochmal ausführlich erklärt bekommen willst, dann schau hier unser Video an!