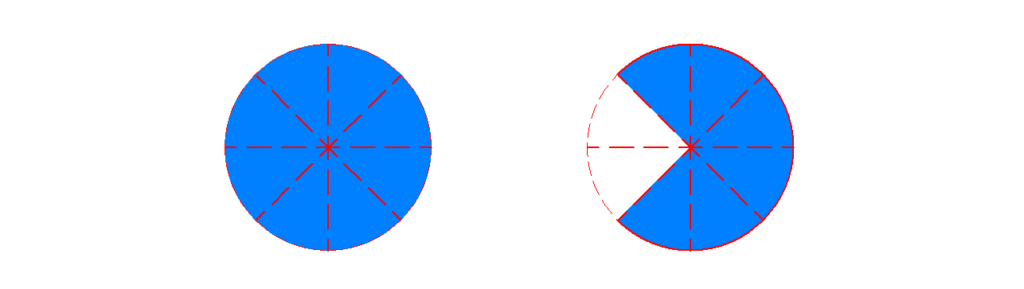
Unechter Bruch
Du willst wissen, was ein unechter Bruch ist und wie du ihn in eine gemischte Zahl umwandeln kannst? Dann bist du hier genau richtig! Schau dir doch auch unser Video zu dem Thema an!
Inhaltsübersicht
Was ist ein unechter Bruch?
Ein unechter Bruch ist ein Bruch , bei dem die Zahl oben (Zähler) größer oder gleich der Zahl unten (Nenner) ist.
Ein Beispiel für einen unechten Bruch ist
![Rendered by QuickLaTeX.com \[\frac{\textcolor{blue}{7}}{\textcolor{red}{5}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-fbddd325f261a3c8f83a206e90230ce0_l3.png)
Weitere Beispiele für unechte Brüche sind:
![Rendered by QuickLaTeX.com \[\frac{\textcolor{blue}{4}}{\textcolor{red}{3}} \qquad \frac{\textcolor{blue}{5}}{\textcolor{red}{5}} \qquad \frac{\textcolor{blue}{8}}{\textcolor{red}{5}} \qquad \frac{\textcolor{blue}{17}}{\textcolor{red}{13}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-79e96dc5cfc2b593b8bcbeb0c78d8f98_l3.png)
Echter und unechter Bruch
Was unterscheidet eigentlich einen unechten Bruch von einem echten Bruch?
Bei einem echten Bruch ist der Zähler kleiner als der Nenner. Beispiele dafür sind:
![Rendered by QuickLaTeX.com \[\frac{\textcolor{blue}{1}}{\textcolor{red}{2}} \qquad \frac{\textcolor{blue}{2}}{\textcolor{red}{4}} \qquad \frac{\textcolor{blue}{3}}{\textcolor{red}{9}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-5f333f2f7f8b8b728cd7f7c03b162158_l3.png)
Merke: Rechnest du einen Bruch in eine Kommazahl um, dann gilt
-
echte Brüche sind kleiner als 1. (Beispiel:
 )
) -
unechte Brüche sind größer oder gleich 1. (Beispiel:
 = 1,33)
= 1,33)
Auf einem Zahlenstrahl sieht das deshalb so aus:
Die echten Brüche befinden sich alle links von der 1, die unechten Brüche liegen alle rechts davon.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Unechten Bruch in gemischte Zahl umwandeln
Eine gemischte Zahl besteht aus einer ganzen Zahl und einem echten Bruch. Sie kann zum Beispiel so aussehen:
![Rendered by QuickLaTeX.com \[ \textcolor{olive}{2} \frac{\textcolor{blue}{1}}{\textcolor{red}{4}} \qquad \textcolor{olive}{1} \frac{\textcolor{blue}{2}}{\textcolor{red}{3}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-9f5b5e604aced229ee0bd6c1352cc881_l3.png)
Oft musst du Aufgaben lösen, bei denen du einen unechten Bruch in eine gemischte Zahl umwandeln musst.
Schau dir das gleich mal an einem Beispiel an: Stell dir vor, du hast für deinen Geburtstag 2 Kuchen gebacken, die jeweils aus 8 Stücken bestehen. Deine Gäste haben zusammen 14 Kuchenstücke gegessen. Das sind dann also insgesamt  .
.
Das möchtest du jetzt auch als gemischten Bruch aufschreiben. Auf dem Bild kannst du leicht erkennen: Deine Gäste haben 1 ganzen Kuchen gegessen und bei dem anderen nur 6 von 8 Stücken. Als gemischte Zahl erhältst du deshalb 1  . Es gilt also:
. Es gilt also:
![Rendered by QuickLaTeX.com \[\frac{\textcolor{blue}{14}}{\textcolor{red}{8}} = \textcolor{olive}{1} \frac{\textcolor{blue}{6}}{\textcolor{red}{8}}\]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-19448df6689beecf4a617b81dea696ff_l3.png)
Gar nicht so schwer, oder?
Du kannst diese Art von Aufgaben auch rechnerisch lösen, indem du mit Rest teilst . Schau dir das am Beispiel von diesem Bruch an:
![Rendered by QuickLaTeX.com \[\frac{\textcolor{blue}{9}}{\textcolor{red}{4}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-eaaf3af8e28c9e97248241df818c00a5_l3.png)
- Frage dich zuerst, wie oft die 4 in die 9 passt. Sie tut es genau 2 Mal! Denn 2 • 4 ist nur 8, während 3 • 4 schon 12 wäre. Die 2 wird die ganze Zahl in deiner gemischten Zahl sein.
- Jetzt musst du nur noch den Rest bestimmen. Das machst du, indem du die 2 • 4 von der 9, abziehst. Also 9 – (2 • 4) = 9 – 8 = 1. Die 1 ist dein Rest!
- Schreibe jetzt deine komplette Rechnung auf:
9 : 4 = 2 Rest 1
Jetzt bist du schon fast am Ziel. Du brauchst nur noch den Bruch hinter der 2. Dieser besteht aus dem Rest 1 als neuem Zähler, während der Nenner 4 gleich bleibt. Du erhältst also:
![Rendered by QuickLaTeX.com \[\frac{\textcolor{blue}{9}}{\textcolor{red}{4}} = \textcolor{olive}{2} \frac{\textcolor{magenta}{1}}{\textcolor{red}{4}} \]](https://blog.assets.studyflix.de/wp-content/ql-cache/quicklatex.com-447eaf896168712320e157dd9a09a342_l3.png)
Negative unechte Brüche
Brüche können natürlich auch negativ, also kleiner als 0, sein. Um einen negativen, unechten Bruch zu erkennen, muss die Definition etwas angepasst werden.
Du nennst einen Bruch unecht, wenn der Betrag seines Zählers (oben) größer oder gleich groß ist wie der Betrag seines Nenners (unten).
Den Betrag einer Zahl erhältst du, indem du ihr Vorzeichen weglässt. Der Betrag von +3 und -3 ist zum Beispiel beide Male 3. Wenn du den Betrag einer Zahl meinst, schreibst du auch Striche |…| um sie herum. Es gilt also: |+3| = |-3| = 3.
Mithilfe dieser Definition kannst du jetzt auch negative, unechte Brüche bestimmen:
 ist ein unechter Bruch, denn |-7| > | 5 |. (7 > 5)
ist ein unechter Bruch, denn |-7| > | 5 |. (7 > 5)
 ist ein unechter Bruch, da |-4| > |-2|. (4 > 2)
ist ein unechter Bruch, da |-4| > |-2|. (4 > 2)
 ist kein unechter Bruch, da | 1 | < |-3|. (1 < 3)
ist kein unechter Bruch, da | 1 | < |-3|. (1 < 3)
Hast du einen Bruch, bei dem vorne ein Minus als Vorzeichen steht, kannst du es dir einfach wegdenken.
 ist ein unechter Bruch, da
ist ein unechter Bruch, da  ein unechter Bruch ist.
ein unechter Bruch ist.
Bruchrechnen
Super, jetzt kennst du dich mit unechten Brüchen aus! Du sollst in der Schule aber nicht nur unechte Brüche bestimmen, sondern auch mit ihnen rechnen? Kein Problem, schau dir doch einfach unser Video zum Bruchrechnen an!