Wie finde ich den Hauptnenner, wenn ich 3 Brüche auf denselben Nenner bringen muss?

Den Hauptnenner für 3 Brüche findest du, indem du eine Zahl suchst, die durch alle drei Nenner ohne Rest teilbar ist und davon die kleinste nimmst. Zuerst schreibst du Vielfache des größten Nenners auf. Dann prüfst du, welches Vielfache auch in den anderen Reihen liegt. Zum Beispiel bei 2, 3, 4 ist 12 der Hauptnenner.

Wie erweitere ich einen Bruch so, dass der Nenner 10 oder 100 ist?

Einen Bruch erweiterst du auf den Nenner 10 oder 100, indem du den Nenner mit einer Zahl malnimmst, bis 10 oder 100 herauskommt und denselben Faktor auch im Zähler malnimmst. Zum Beispiel wird zu , weil . Dagegen klappt nicht auf 10, weil es keine ganze Zahl gibt die 6 zu 10 macht.

Wie erweitere ich eine gemischte Zahl?

Eine gemischte Zahl erweiterst du, indem du sie zuerst in einen Bruch umwandelst und erst dann Zähler und Nenner mit derselben Zahl malnimmst. Zuerst machst du aus den Bruch , weil . Dann erweiterst du zum Beispiel mit 4 zu . Danach kannst du wieder zurück in eine gemischte Zahl umwandeln, wenn du willst.

Video

Quiz

Hier geht's zum Video „Brüche kürzen“

Brüche erweitern

Wichtige Inhalte in diesem Video

Wie erweitert man Brüche?

(00:12)

Erweitern von Brüchen

(01:13)

Erweiterungszahl ermitteln

(01:37)

Brüche auf einen Hauptnenner erweitern

(02:49)

In diesem Video zeigen wir dir, wie du Brüche erweitern kannst und was du dabei beachten musst. Du möchtest anschauliche Beispiele sehen? Dann guck dir unser Video dazu an!

Klasse 5

Klasse 6

Klasse 7

Inhaltsübersicht

Wie erweitert man Brüche?

im Videozur Stelle im Video springen

(00:12)

Du erweiterst einen Bruch, indem du Zähler und Nenner mit der gleichen Zahl multiplizierst.

Brüche erweitern, Bruch erweitern, erweitern von brüchen, wie erweitert man brüche, nenner erweitern, mathe erweitern, erweitern von brüchen erklärung, Kreis, Anteile, Kreissektoren, Erweitern, Kürzen — Erweitern von Brüchen

Dabei verändert sich der Wert des Bruchs nicht: Es ist egal, ob du bei einer Pizza 1 von 3 Stücken nimmst oder 2 von 6 Stücken — du hast beides mal gleich viel Pizza!

Schau dir jetzt an, wie genau du einen Bruch erweitern kannst.

Erweitern von Brüchen

im Videozur Stelle im Video springen

(01:13)

Du sollst zum Beispiel den Bruch $\frac{\textcolor{blue}{2}}{\textcolor{red}{3}}$ mit 3 erweitern.

Dazu musst du Zähler und Nenner mit 3 multiplizieren. Du rechnest also:

im Zähler: 2 ⋅ 3 = 6
im Nenner: 3 ⋅ 3 = 9.

$\cfrac{\textcolor{blue}{2}\textcolor{teal}{\,\cdot3}}{\textcolor{red}{3}\textcolor{teal}{\,\cdot3}} = \cfrac{6}{9}$

Dabei erhältst du den neuen Bruch $\frac{6}{9}$ .

Achtung: Mit 0 darfst du nie erweitern!

Hinweis: Kürzen und Erweitern von Brüchen

Das Gegenteil vom Erweitern ist das Kürzen. Dabei teilst du im Zähler und im Nenner durch die gleiche Zahl. Wie das geht, zeigen wir dir weiter unten in diesem Artikel.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Erweiterungszahl ermitteln

im Videozur Stelle im Video springen

(01:37)

Bisher haben wir dir die Erweiterungszahl vorgegeben. Normalerweise musst du sie allerdings selbst herausfinden. Um Brüche zu addieren und zu subtrahieren , müssen sie den gleichen Nenner haben.

Beispiel 1

Bringe die Brüche $\frac{\textcolor{blue}{1}}{\textcolor{red}{3}}$ und $\frac{\textcolor{blue}{5}}{\textcolor{red}{9}}$ auf einen Nenner.

Dazu überlegst du dir zunächst, ob es eine Zahl gibt, mit der du den kleineren Nenner 3 malnehmen kannst, sodass er 9 wird. Da 3 ⋅ 3 = 9 ist, kannst du den Bruch 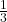$\frac{1}{3}$ mit 3 erweitern.

Brüche erweitern, Brüche erweitern und kürzen, Erweiterungszahl, Bruchrechnen, Brüche — Bruch erweitern

Du hast die Brüche nun auf den gemeinsamen Nenner 9 gebracht.

Beispiel 2

Bringe die Brüche $\frac{\textcolor{blue}{1}}{\textcolor{red}{6}}$ und $\frac{\textcolor{blue}{2}}{\textcolor{red}{5}}$ auf einen Nenner.

Wenn dir nicht direkt ein gemeinsames Vielfaches der beiden Nenner auffällt, kannst du die Brüche auch einfach mit dem Nenner des jeweils anderen Bruchs erweitern.

Brüche erweitern, Erweitern, Bruchrechnen, Brüche, Erweiterungszahl — Brüche erweitern

Jetzt haben beide Brüche den gleichen Nenner 30.

Brüche auf einen Hauptnenner erweitern

im Videozur Stelle im Video springen

(02:49)

Wenn du Brüche addieren und subtrahieren willst, musst du sie auf ihren Hauptnenner erweitern.

Schau dir gleich ein Beispiel dazu an: Die Brüche $\frac{\textcolor{blue}{2}}{\textcolor{red}{4}}$ und $\frac{\textcolor{blue}{1}}{\textcolor{red}{3}}$ sollen auf einen Hauptnenner gebracht werden. Der Hauptnenner ist die kleinste Zahl, die in der 3er-Reihe und in der 4er-Reihe vorkommt (kleinstes gemeinsames Vielfaches).

1. Notiere dir alle Vielfachen der Nenner (3er- und 4er-Reihe)

Vielfache von 4: { 4, 8, 12, 16, 20, …}

Vielfache von 3: {3, 6, 9, 12, 15, …}

2. Finde die kleinste Zahl, die in beiden Aufzählungen vorkommt:

Vielfache von 4: { 4, 8, 12, 16, 20, …}

Vielfache von 3: {3, 6, 9, 12, 15, …}

Die 12 ist das kleinste gemeinsame Vielfache von 4 und 3. Du kannst also auf den Hauptnenner 12 erweitern.

3. Erweitere die Brüche auf den Hauptnenner 12

Der Bruch $\frac{\textcolor{blue}{2}}{\textcolor{red}{4}}$ bekommt den Nenner 12, wenn du ihn mit 3 erweiterst, da 4 ⋅ 3 = 12 ist.

$\cfrac{\textcolor{blue}{2}\textcolor{teal}{\,\cdot3}}{\textcolor{red}{4}\textcolor{teal}{\,\cdot3}} = \cfrac{6}{\textcolor{orange}{12}}$

Den Bruch $\frac{\textcolor{blue}{1}}{\textcolor{red}{3}}$ musst du nun mit 4 erweitern.

$\cfrac{\textcolor{blue}{1}\textcolor{teal}{\,\cdot4}}{\textcolor{red}{3}\textcolor{teal}{\,\cdot4}} = \cfrac{4}{\textcolor{orange}{12}}$

Brüche erweitern — häufigste Fragen

(ausklappen)

Wie finde ich den Hauptnenner, wenn ich 3 Brüche auf denselben Nenner bringen muss?

Den Hauptnenner für 3 Brüche findest du, indem du eine Zahl suchst, die durch alle drei Nenner ohne Rest teilbar ist und davon die kleinste nimmst. Zuerst schreibst du Vielfache des größten Nenners auf. Dann prüfst du, welches Vielfache auch in den anderen Reihen liegt. Zum Beispiel bei 2, 3, 4 ist 12 der Hauptnenner.
Wie erweitere ich einen Bruch so, dass der Nenner 10 oder 100 ist?

Einen Bruch erweiterst du auf den Nenner 10 oder 100, indem du den Nenner mit einer Zahl malnimmst, bis 10 oder 100 herauskommt und denselben Faktor auch im Zähler malnimmst. Zum Beispiel wird zu , weil $5 \cdot 2 = 10$ . Dagegen klappt nicht auf 10, weil es keine ganze Zahl gibt die 6 zu 10 macht.
Wie erweitere ich eine gemischte Zahl?

Eine gemischte Zahl erweiterst du, indem du sie zuerst in einen Bruch umwandelst und erst dann Zähler und Nenner mit derselben Zahl malnimmst. Zuerst machst du aus $2\;1/3$ den Bruch , weil $2 \cdot 3 + 1 = 7$ . Dann erweiterst du zum Beispiel mit 4 zu . Danach kannst du wieder zurück in eine gemischte Zahl umwandeln, wenn du willst.

Brüche erweitern und kürzen

Um Brüche auf einen Nenner zu bringen, kannst du sie Erweitern und Kürzen. Beim Kürzen teilst du Zähler und Nenner durch die gleiche Zahl.

Beim Erweitern werden aus wenigen großen Stücken, mehrere kleine Stücke. Beim Kürzen fügst du die vielen kleinen Stücke wieder zu wenigen großen Stücken zusammen.

Erweitern, Kürzen, Bruchrechnen, Bruchrechnung, Brüche kürzen und erweitern, Brüche erweitern, Brüche kürzen, Brüche, Bruch — Brüche erweitern und kürzen

Grundsätzlich verändert sich der Wert der Brüche beim Erweitern und Kürzen nicht. Es macht also keinen Unterschied, ob du $\frac{\textcolor{blue}{1}}{\textcolor{red}{2}}$ , $\frac{\textcolor{blue}{2}}{\textcolor{red}{4}}$ oder $\frac{\textcolor{blue}{4}}{\textcolor{red}{8}}$ von einer Pizza bekommst.