Video anzeigen

Brüche addieren

Wichtige Inhalte in diesem Video

Brüche durch Kürzen auf einen Nenner bringen

Brüche durch Erweitern auf einen Nenner bringen

Wie kannst du Brüche addieren? Unsere Aufgaben und Beispiele zum Bruchrechnen Addieren erklären es dir hier im Beitrag und dem Video .

Inhaltsübersicht

Wie addiert man Brüche?

im Videozur Stelle im Video springen

(00:12)

$\cfrac{\textcolor{blue}{3}}{\textcolor{red}{8}} + \cfrac{\textcolor{blue}{2}}{\textcolor{red}{8}} = \cfrac{\textcolor{blue}{3 + 2}}{\textcolor{red}{8}} = \cfrac{\textcolor{blue}{5}}{\textcolor{red}{8}}$

Du kannst zwei Brüche addieren, wenn sie den gleichen Nenner (untere Zahl) haben.

Dazu addierst du einfach die beiden Zähler (obere Zahl). Der Nenner bleibt gleich.

Aber oft musst du in Mathe Brüche plus rechnen, die verschiedene Nenner haben (ungleichnamige Brüche). Wenn du ungleichnamige Brüche addieren willst, musst du sie erst auf den gleichen Nenner bringen. Dazu erweiterst du die Brüche.

Anschließend kannst du den Bruch addieren wie im ersten Beispiel.

$\cfrac{2}{\textcolor{olive}{3}} + \cfrac{1}{\textcolor{orange}{4}} = \cfrac{2 \cdot \textcolor{orange}{4}}{\textcolor{olive}{3} \cdot \textcolor{orange}{4}} + \cfrac{1 \cdot \textcolor{olive}{3}}{\textcolor{orange}{4} \cdot \textcolor{olive}{3}} = \cfrac{8}{\textcolor{red}{12}} + \cfrac{3}{\textcolor{red}{12}} = \cfrac{11}{\textcolor{red}{12}}$

Beim Addieren von Brüchen hilft dir das Erweitern mit dem anderen Nenner. Im Beispiel hast du die Drittel mit 4 und die Viertel mit 3 erweitert.

Gleichnamige Brüche addieren

Brüche sind gleichnamig, wenn sie denselben Nenner haben.

Beispiel 1

Im ersten Beispiel sollst du folgende gleichnamige Brüche zusammenzählen (addieren).

$\cfrac{\textcolor{blue}{3}}{\textcolor{red}{7}}+\cfrac{\textcolor{blue}{2}}{\textcolor{red}{7}}$

Beide Brüche haben den gleichen Nenner 7. Du rechnest also im Zähler 3 + 2 = 5.

$\cfrac{\textcolor{blue}{3}}{\textcolor{red}{7}}+\cfrac{\textcolor{blue}{2}}{\textcolor{red}{7}} = \cfrac{\textcolor{blue}{3}\,+\,\textcolor{blue}{2}}{\textcolor{red}{7}} = \cfrac{\textcolor{blue}{5}}{\textcolor{red}{7}}$

Beispiel 2

Führe wieder eine Bruchaddition durch.

$\cfrac{\textcolor{blue}{4}}{\textcolor{red}{13}}+\cfrac{\textcolor{blue}{6}}{\textcolor{red}{13}} = \cfrac{\textcolor{blue}{4}\,+\,\textcolor{blue}{6}}{\textcolor{red}{13}} = \cfrac{\textcolor{blue}{10}}{\textcolor{red}{13}}$

Ungleichnamige Brüche addieren

Damit du ungleichnamige Brüche zusammen rechnen kannst, musst du sie zuerst durch Kürzen oder Erweitern auf denselben Nenner bringen. %hier ist was schief :D <span style="color: #ff00ff;">Done</span>

Brüche durch Kürzen auf einen Nenner bringen

im Videozur Stelle im Video springen

(01:06)

Manchmal kannst du die Brüche durch Kürzen auf einen gemeinsamen Nenner, den Hauptnenner, bringen.

Beispiel

$\cfrac{4}{\textcolor{red}{6}} + \cfrac{1}{\textcolor{red}{3}}$

1. Brüche auf gleichen Nenner bringen:

$\cfrac{4}{6} = \cfrac{4\textcolor{teal}{\,:2}}{6\textcolor{teal}{\,:2}}= \cfrac{2}{3}$

2. Brüche addieren:

$\cfrac{4}{6} + \cfrac{1}{3}=\cfrac{2}{\textcolor{red}{3}} + \cfrac{1}{\textcolor{red}{3}} =\cfrac{2\,+\,1}{\textcolor{red}{3}}= \cfrac{3}{\textcolor{red}{3}}$

3. Ergebnis kürzen: Zuletzt kannst du das Ergebnis kürzen.

$\cfrac{3}{\textcolor{red}{3}} = 1$

Brüche durch Erweitern auf einen Nenner bringen

im Videozur Stelle im Video springen

(02:14)

Manche Brüche kannst du aber nicht mehr kürzen.

Was beim Bruch Addieren aber immer funktioniert, ist das Erweitern. Dazu multiplizierst du Zähler und Nenner mit derselben Zahl. So kommst du auf einen gemeinsamen Nenner und kannst die Brüche plus rechnen.

Beispiel 1

Führe die Bruch Addition durch.

$\cfrac{2}{10}+\cfrac{1}{2}$

1.Brüche auf gleichen Nenner bringen:

$\cfrac{1\textcolor{olive}{\,\cdot \,5}}{2\textcolor{olive}{\,\cdot \,5}} = \cfrac{5}{10}$

2. Brüche addieren:

$\cfrac{2}{\textcolor{red}{10}} + \cfrac{5}{\textcolor{red}{10}} = \cfrac{7}{10}$

3. Ergebnis kürzen: Fällt hier weg, weil dein Ergebnis schon vollständig gekürzt ist.

Beispiel 2

Berechne folgende Aufgabe zur Addition von Brüchen.

$\cfrac{1}{5} + \cfrac{2}{6}$

1. Brüche erweitern: Erweitere am besten mit dem jeweils anderen Nenner.

$\cfrac{1}{\textcolor{olive}{5}} + \cfrac{2}{\textcolor{orange}{6}} = \cfrac{1\textcolor{orange}{\,\cdot\,6}}{5\textcolor{orange}{\,\cdot\,6}} + \cfrac{2\textcolor{olive}{\,\cdot\,5}}{6\textcolor{olive}{\,\cdot\,5}} = \cfrac{6}{30} + \cfrac{10}{30}$

2. Brüche addieren:

$\cfrac{6}{\textcolor{red}{30}} + \cfrac{10}{\textcolor{red}{30}} = \cfrac{6\, + \,10}{\textcolor{red}{30}} = \cfrac{16}{30}$

3. Ergebnis kürzen:

$\cfrac{16}{30} = \cfrac{16\textcolor{teal}{\,:2}}{30\textcolor{teal}{\,:2}} = \cfrac{8}{15}$

Gemischte Brüche addieren

im Videozur Stelle im Video springen

(03:28)

Damit du gemischte Brüche addieren kannst, musst du sie zuerst in Brüche umwandeln. Das heißt du ziehst die Zahl vor dem Bruch auf den Zähler.

Beispiel

Schauen wir uns die Bruchaddition mit gemischten Brüchen an folgendem Beispiel an.

$1\cfrac{2}{5} + \cfrac{3}{5}$ %muss der Punkt raus <span style="color: #ff00ff;">Ja, done</span>

1. Gemischte Zahl in Bruch umwandeln: Multipliziere zuerst die ganze Zahl mit dem Nenner und addiere sie anschließend zum Zähler.

$\textcolor{blue}{1}\cfrac{2}{\textcolor{red}{5}} = \cfrac{\textcolor{blue}{1}\,\cdot\,\textcolor{red}{5} + 2}{\textcolor{red}{5}} = \cfrac{7}{5}$

2. Brüche auf einen Nenner bringen: Die Brüche sind schon gleichnamig mit dem Hauptnenner 5.

3. Brüche addieren:

$1\cfrac{2}{5} + \cfrac{3}{5} = \cfrac{7}{\textcolor{red}{5}} + \cfrac{3}{\textcolor{red}{5}} = \cfrac{10}{\textcolor{red}{5}}$

4. Ergebnis kürzen:

$\cfrac{10\textcolor{teal}{\,:5}}{5\textcolor{teal}{\,:5}}= \cfrac{2}{1} = 2$

Brüche mit ganzen Zahlen addieren

Damit du ganze Zahlen mit Brüchen addieren kannst, musst du die Zahl zuerst in einen Bruch umwandeln.

Beispiel

Hier sollst du Brüche mit ganzen Zahlen addieren.

$\textcolor{blue}{2} + \cfrac{1}{6}$

1.Zahl in Bruch umwandeln: Ganze Zahlen kannst du leicht in einen Bruch umwandeln. Dazu schreibst du die ganze Zahl auf den Zähler: hier also die 2. Der Nenner ist bei ganzen Zahlen immer die 1.

$\textcolor{blue}{2}+ \cfrac{1}{6} = \cfrac{\textcolor{blue}{2}}{1} + \cfrac{1}{6}$

2.Brüche auf einen Nenner bringen:

$\cfrac{2\textcolor{olive}{\,\cdot6}}{1\textcolor{olive}{\,\cdot6}} + \cfrac{1}{6}= \cfrac{12}{\textcolor{red}{6}} + \cfrac{1}{\textcolor{red}{6}}$

3.Brüche addieren:

$\cfrac{12}{\textcolor{red}{6}} + \cfrac{1}{\textcolor{red}{6}} = \cfrac{13}{\textcolor{red}{6}}$

4. Brüche kürzen: Fällt hier weg.

Brüche addieren Aufgaben

Jetzt kannst du noch ein bisschen die Addition von Brüchen üben.

Aufgabe 1: Gleichnamige Brüche addieren

$a)\, \frac{3}{11} + \frac{6}{11}$

$b)\, \frac{2}{9} + \frac{5}{9}$

Aufgabe 2: Ungleichnamige Brüche addieren

$a)\, \frac{3}{16} + \frac{2}{4}$

$b)\, \frac{4}{25} + \frac{2}{5}$

Aufgabe 3: Gemischte Brüche addieren

$a)\, \frac{3}{6} + 2\frac{1}{6}$

$b)\, 4\frac{3}{6} + 1\frac{5}{8}$

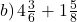
Aufgabe 4: Brüche mit ganzen Zahlen addieren

$a)\, \frac{7}{11} + 3$

$b)\, 2 + \frac{3}{8}$

Im Folgenden kannst du überprüfen, ob du zum Brüche Addieren zu allen Aufgaben die richtige Lösung gefunden hast.

Lösung

Lösung 1: Gleichnamige Brüche addieren

$a)\, \frac{3}{\textcolor{red}{11}} + \frac{6}{\textcolor{red}{11}}= \frac{3\,+\,6}{\textcolor{red}{11}}=\frac{9}{\textcolor{red}{11}}$

(Zähler addieren)

$b)\, \frac{2}{\textcolor{red}{9}}+ \frac{5}{\textcolor{red}{9}}= \frac{2\,+\,5}{\textcolor{red}{9}} = \frac{7}{\textcolor{red}{9}}$

Lösung 2: Ungleichnamige Brüche addieren

$a)\, \frac{3}{16} + \frac{2}{4} = \frac{3}{16} + \frac{2\textcolor{olive}{\,\cdot4}}{4\textcolor{olive}{\,\cdot4}}= \frac{3}{\textcolor{red}{16}} + \frac{8}{\textcolor{red}{16}} = \frac{11}{\textcolor{red}{16}}$

$b)\, \frac{2}{5} + \frac{5\,\textcolor{teal}{\,:5}}{25\,\textcolor{teal}{\,:5}} = \frac{2}{\textcolor{red}{5}} + \frac{1}{\textcolor{red}{5}} = \frac{3}{\textcolor{red}{5}}$

(Brüche zuerst durch Erweitern/Kürzen auf einen Nenner bringen und danach Zähler addieren)

Lösung 3: Gemischte Brüche addieren

$a)\, \frac{3}{6} + \textcolor{blue}{2}\frac{1}{\textcolor{red}{6}} = \frac{3}{6} +\frac{\textcolor{blue}{2}\,\cdot\,\textcolor{red}{6}\,+\,1}{\textcolor{red}{6}} = \frac{3}{\textcolor{red}{6}} + \frac{13}{\textcolor{red}{6}} = \frac{16}{\textcolor{red}{6}} = 2\frac{2}{3}$

(Gemischte Zahl zuerst in Bruch umwandeln und danach Zähler addieren)

$b)\, \textcolor{blue}{4}\frac{3}{\textcolor{red}{6}} + \textcolor{blue}{1}\frac{5}{\textcolor{red}{8}} = \frac{\textcolor{blue}{4}\,\cdot\,\textcolor{red}{6}\,+\,3}{\textcolor{red}{6}} + \frac{\textcolor{blue}{1}\,\cdot\,\textcolor{red}{8}\,+\,5}{\textcolor{red}{8}}=\frac{27\textcolor{teal}{\,\cdot4}}{6\textcolor{teal}{\,\cdot4}} + \frac{13\textcolor{teal}{\,\cdot3}}{8\textcolor{teal}{\,\cdot3}}= \frac{108}{\textcolor{red}{24}} + \frac{39}{\textcolor{red}{24}}=\frac{147\textcolor{teal}{\,:3}}{\textcolor{red}{24}\textcolor{teal}{\,:3}} = {\frac{49}{8}$

Lösung 4: Brüche mit ganzen Zahlen addieren

$a) \frac{7}{11} + \textcolor{blue}{3} = \frac{7}{11} + \frac{3\textcolor{olive}{\,\cdot11}}{1\textcolor{olive}{\,\cdot11}} = \frac{7}{\textcolor{red}{11}} + \frac{33}{\textcolor{red}{11}} = \frac{40}{\textcolor{red}{11}}$

(Ganze Zahl zuerst in einen Bruch umwandeln)

$b)\, \textcolor{blue}{2} + \frac{3}{8} =\frac{2\textcolor{olive}{\,\cdot8}}{1\textcolor{olive}{\,\cdot8}} + \frac{3}{8} = \frac{16}{\textcolor{red}{8}} + \frac{3}{\textcolor{red}{8}}= \frac{19}{\textcolor{red}{8}} = 2\frac{3}{8}$

Brüche addieren und subtrahieren

Brüche addieren und subtrahieren funktioniert im Grunde genommen gleich. Genauso wie bei der Addition von Brüchen, müssen die Brüche also auch bei der Subtraktion den gleichen Nenner haben. Ist das der Fall, rechnest du einfach den Zähler des ersten Bruchs minus den Zähler des zweiten Bruchs. Im Prinzip musst du einfach negative Brüche addieren.

$\cfrac{\textcolor{orange}{3}}{\textcolor{red}{4}} \textcolor{teal}{-} \cfrac{\textcolor{teal}{2}}{\textcolor{red}{4}} = \cfrac{\textcolor{orange}{3}}{\textcolor{red}{4}} + \cfrac{\textcolor{teal}{-2}}{\textcolor{red}{4}} = \cfrac{\textcolor{orange}{3} \textcolor{teal}{-2}}{\textcolor{red}{4}} = \cfrac{\textcolor{orange}{1}}{\textcolor{red}{4}}$

Auch zum Brüche Subtrahieren haben wir ein extra Video für dich. Dort zeigen wir dir viele weitere Beispiele. Schau es dir an!

Mathematische Grundlagen

Mathe Grundschule

Mathematische Grundlagen

Zahlenlehre

Mathematische Grundlagen

Teilbarkeit

Mathematische Grundlagen

Dreisatz

Mathematische Grundlagen

Dezimalzahlen

Mathematische Grundlagen

Rechnen

Mathematische Grundlagen

Brüche

Mathematische Grundlagen

Bruchrechnung

Mathematische Grundlagen

Rechenregeln

Mathematische Grundlagen

Formeln und Terme

Mathematische Grundlagen

Binomische Formeln

Mathematische Grundlagen

Potenzen & Wurzeln

Brüche addieren

Wie addiert man Brüche?

Gleichnamige Brüche addieren

Beispiel 1

Beispiel 2

Ungleichnamige Brüche addieren

Brüche durch Kürzen auf einen Nenner bringen

Beispiel

Brüche durch Erweitern auf einen Nenner bringen

Beispiel 1

Beispiel 2

Gemischte Brüche addieren

Beispiel

Brüche mit ganzen Zahlen addieren

Beispiel

Brüche addieren Aufgaben

Lösung

Brüche addieren und subtrahieren

Beliebte Inhalte aus dem Bereich Mathematische Grundlagen

Mathematische Grundlagen Mathe Grundschule

Mathematische Grundlagen Zahlenlehre

Mathematische Grundlagen Teilbarkeit

Mathematische Grundlagen Dreisatz

Mathematische Grundlagen Dezimalzahlen

Mathematische Grundlagen Rechnen

Mathematische Grundlagen Brüche

Mathematische Grundlagen Bruchrechnung

Mathematische Grundlagen Rechenregeln

Mathematische Grundlagen Formeln und Terme

Mathematische Grundlagen Binomische Formeln

Mathematische Grundlagen Potenzen & Wurzeln

Brüche addieren

Wie addiert man Brüche?

Gleichnamige Brüche addieren

Beispiel 1

Beispiel 2

Ungleichnamige Brüche addieren

Brüche durch Kürzen auf einen Nenner bringen

Beispiel

Brüche durch Erweitern auf einen Nenner bringen

Beispiel 1

Beispiel 2

Gemischte Brüche addieren

Beispiel

Brüche mit ganzen Zahlen addieren

Beispiel

Brüche addieren Aufgaben

Lösung

Brüche addieren und subtrahieren

Beliebte Inhalte aus dem Bereich Mathematische Grundlagen

Mathematische Grundlagen

Mathe Grundschule

Mathematische Grundlagen

Zahlenlehre

Mathematische Grundlagen

Teilbarkeit

Mathematische Grundlagen

Dreisatz

Mathematische Grundlagen

Dezimalzahlen

Mathematische Grundlagen

Rechnen

Mathematische Grundlagen

Brüche

Mathematische Grundlagen

Bruchrechnung

Mathematische Grundlagen

Rechenregeln

Mathematische Grundlagen

Formeln und Terme

Mathematische Grundlagen

Binomische Formeln

Mathematische Grundlagen

Potenzen & Wurzeln