Wie multipliziere ich negative Brüche?

Negative Brüche multiplizierst du, indem du zuerst auf die Minuszeichen schaust und dann ganz normal Zähler mal Zähler und Nenner mal Nenner rechnest. Haben beide Faktoren ein Minus, wird das Ergebnis plus. Hat nur einer ein Minus, wird das Ergebnis minus. Zum Beispiel: .

Wie schreibe ich einen unechten Bruch als gemischte Zahl?

Einen unechten Bruch schreibst du als gemischte Zahl, indem du den Zähler durch den Nenner teilst. Die ganze Zahl ist das Ergebnis ohne Rest. Der Rest wird der neue Zähler und der Nenner bleibt gleich. Zum Beispiel: Rest , also .

Was rechne ich zuerst, wenn in einer Aufgabe mit Brüchen mal und plus vorkommen?

Bei Brüchen mit mal und plus rechnest du zuerst alle Multiplikationen und danach die Additionen. Danach bringst du beim Addieren die Brüche auf einen gleichen Nenner. Zum Beispiel: .

Video

Quiz

Hier geht's zum Video „Brüche kürzen“

Brüche multiplizieren

Wichtige Inhalte in diesem Video

Multiplikation von Brüchen (Bruch mal Bruch)

(00:11)

Brüche multiplizieren mit ganzen Zahlen

(00:57)

Gemischte Brüche mit Bruch multiplizieren

(02:16)

Mehrere Brüche multiplizieren

(03:04)

Beim Bruchrechnen kannst du Brüche mit ganzen Zahlen oder mit anderen Brüchen multiplizieren. Wie das funktioniert und was du dabei beachten musst erklären wir dir im Video .

Klasse 5

Klasse 6

Klasse 7

Inhaltsübersicht

Wie multipliziert man Brüche?

Beim Multiplizieren von zwei Brüchen, multiplizierst du den Zähler des ersten Bruchs mit dem Zähler des zweiten Bruchs. Anschließend multiplizierst du den Nenner des ersten Bruchs mit dem Nenner des zweiten Bruchs.

Schauen wir uns direkt Beispiele dazu an!

Multiplikation von Brüchen (Bruch mal Bruch)

im Videozur Stelle im Video springen

(00:11)

Du kannst einen Bruch mit einem anderen Bruch multiplizieren, indem du Zähler mit Zähler und Nenner mit Nenner multiplizierst.

$\frac{\textcolor{blue}{Zähler}}{\textcolor{red}{Nenner}}\cdot\frac{\textcolor{blue}{Zähler}}{\textcolor{red}{Nenner}}=\frac{\textcolor{blue}{Zähler}\,&\cdot&\,\textcolor{blue}{Zähler}}{\textcolor{red}{Nenner}\,&\cdot&\,\textcolor{red}{Nenner}}$

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich

Beispiel

Im Folgenden sollst du die beiden Brüche $\frac{1}{7}$ und $\frac{2}{3}$ multiplizieren.

Bruch mal Bruch, Brüche multiplizieren, Multiplikation von Brüchen, bruchrechenen — Bruch mal Bruch

1.Zähler mit Zähler multiplizieren: Multipliziere zuerst den Zähler 1 des ersten Bruchs mit dem Zähler 2, des zweiten Bruchs.

$\frac{\textcolor{blue}{1}}{7}\cdot\frac{\textcolor{blue}{2}}{3}&=&\frac{\textcolor{blue}{1\,&\cdot&\,2}}{}&=&\frac{\textcolor{blue}{2}}{}$

2.Nenner mit Nenner multiplizieren: Multipliziere danach den Nenner 7 des ersten Bruchs mit dem Nenner 3 des zweiten Bruchs.

$\frac{\textcolor{blue}{1}}{\textcolor{red}{7}}\cdot\frac{\textcolor{blue}{2}}{\textcolor{red}{3}}&=&\frac{\textcolor{blue}{1\,&\cdot&\,2}}{\textcolor{red}{7\,&\cdot&\,3}}&=&\frac{\textcolor{blue}{2}}{\textcolor{red}{21}}$

Weitere Beispiele

$\frac{5}{23}\cdot\frac{3}{4}=\frac{5\,\cdot\,3}{23\,\cdot\,4}=\frac{15}{92}$

$\frac{8}{13}\cdot\frac{3}{5}=\frac{8\,\cdot\,3}{13\,\cdot\,5}=\frac{24}{65}$

Brüche multiplizieren mit ganzen Zahlen

im Videozur Stelle im Video springen

(00:57)

Beim Brüche multiplizieren mit ganzen Zahlen musst du die Zahl zuerst in einen Bruch umwandeln.

Beispiel

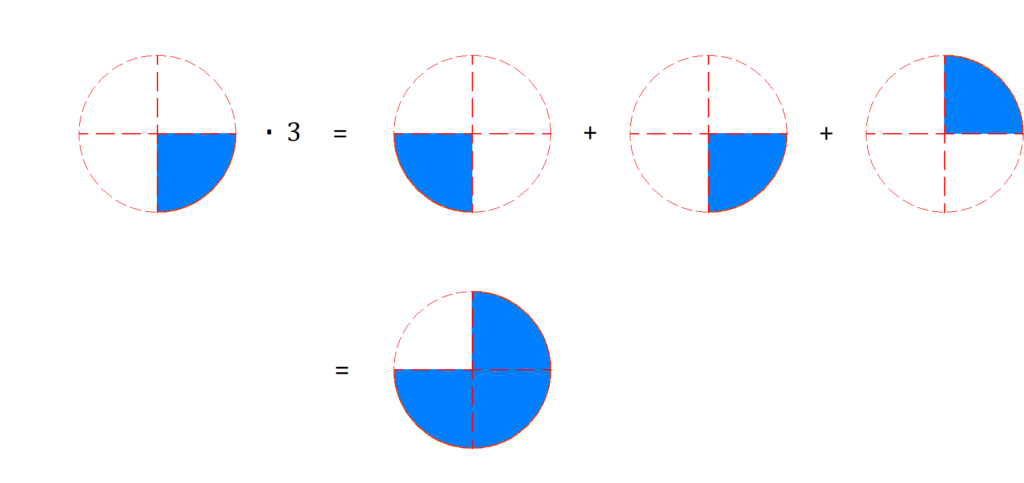
Berechne

$\frac{\textcolor{blue}{1}}{\textcolor{red}{4}}\cdot\textcolor{teal}{3}.$

1.Zahl in Bruch umwandeln: Du kannst alle Zahlen auch als Bruch schreiben. Dazu schreibst du die Zahl 3 als Zähler auf den Bruchstrich. Der Nenner ist bei ganzen Zahlen immer die 1.

$\frac{1}{4}\cdot\textcolor{teal}{3} = \frac{1}{4}\cdot\frac{\textcolor{teal}{3}}{1}$

2.Brüche multiplizieren: Dazu nimmst du wieder Zähler mal Zähler und Nenner mal Nenner.

$\frac{1}{4}\cdot3= \frac{\textcolor{blue}{1}}{\textcolor{red}{4}}\cdot\frac{\textcolor{blue}{3}}{\textcolor{red}{1}}&=&\frac{\textcolor{blue}{1\,&\cdot&\,3}}{\textcolor{red}{4\,&\cdot&\,1}}&=&\frac{\textcolor{blue}{3}}{\textcolor{red}{4}}$

Anschauliche Erklärung: Stell dir vor du hast eine Pizza, die in vier Stücke geschnitten ist. Du isst 1 von 4 Stücken $(\frac{1}{4})$ . Deine beiden Freunde Max und Emma essen auch jeweils ein Stück $(\frac{1}{4}+\frac{1}{4})$ . Zusammen habt ihr dann also 3 der 4 Pizzastücke gegessen $( \frac{1}{4}+\frac{1}{4}+\frac{1}{4})$ . Das sind $\frac{3}{4}$ der kompletten Pizza.

Brüche multiplizieren, Brüche malnehmen, Bruchrechnen, Bruch mit ganzer Zahl multiplizieren — Bruch mit ganzer Zahl multiplizieren

Merke: Bei der Multiplikation von Brüchen musst du ganze Zahlen vor dem Multiplizieren in einen Bruch umwandeln.

$\frac{\textcolor{blue}{a}}{\textcolor{red}{b}}\cdot\textcolor{teal}{c}&=\frac{\textcolor{blue}{a}}{\textcolor{red}{b}}\cdot\frac{\textcolor{teal}{c}}{1} = &\frac{\textcolor{blue}{a}\,\cdot&\,\textcolor{teal}{c}}{\textcolor{red}{b}\,\cdot\,1}=\frac{\textcolor{blue}{a}\,\cdot&\,\textcolor{teal}{c}}{\textcolor{red}{b}}$

Weitere Beispiele

$\textcolor{teal}{4}\cdot\frac{5}{27}&=&\frac{\textcolor{teal}{4}\,\cdot\,5}{27}=\frac{20}{27}$

$\frac{5}{19}\cdot&\textcolor{teal}{3}&=&\frac{5\,\cdot\,\textcolor{teal}{3}}{19}&=&\frac{15}{19}$

Gemischte Brüche mit Bruch multiplizieren

im Videozur Stelle im Video springen

(02:16)

Gemischte Zahlen sind Zahlen, die aus einem Bruch und einer ganzen Zahl bestehen. Wenn du gemischte Brüche multiplizieren willst, musst du sie immer zuerst in einen Bruch umwandeln.

Beispiel

Berechne

$2&\frac{1}{3}\cdot\frac{2}{4}.$

1.Gemischten Bruch umformen: Ziehe zuvor die Zahl 2 mit auf den Zähler, indem du sie mit dem Nenner 3 multiplizierst und zum Zähler 1 addierst. Den Nenner selbst hingegen, lässt du stehen.

$\textcolor{blue}{2}&\frac{1}{\textcolor{red}{3}}=\frac{\textcolor{blue}{2}\,\cdot\,\textcolor{red}{3}+1}{\textcolor{red}{3}}=\frac{7}{3}$

Anschaulich: Du hast 2 ganze Torten, die jeweils aus 3 Stücken bestehen. Das heißt ein Tortenstück ist immer ein Drittel einer Torte. Zusätzlich hast du noch ein Stück von einer dritten Torte ( 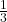$\frac{1}{3}$ ). Insgesamt hast du also 7 Tortenstücke $\frac{7}{3}.$

Bruchrechnen, Brüche multiplizieren, Bruch multiplizieren, Gemischte Zahlen, Gemischte Brüche multiplizieren — Gemischter Bruch

2.Brüche multiplizieren: Das heißt, du hast nun eine normale Multiplikation von zwei Brüchen.

$\frac{\textcolor{blue}{7}}{\textcolor{red}{3}}\cdot\frac{\textcolor{blue}{2}}{\textcolor{red}{4}}&=&\frac{\textcolor{blue}{7\,\cdot\,2}}{\textcolor{red}{3\,\cdot\,4}}=\frac{\textcolor{blue}{14}}{\textcolor{red}{12}}$

3.Ergebnis kürzen: Da der Zähler und der Nenner durch 2 teilbar sind, kannst du jetzt noch kürzen.

$\frac{14}{12}=\frac{14\,\textcolor{teal}{\,:2}}{12\,\textcolor{teal}{\,:2}}=\frac{7}{6}$

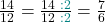
Merke: Beim Multiplizieren von gemischten Brüchen musst du vor dem Multiplizieren die gemischte Zahl in einen Bruch umformen.

$\textcolor{blue}{a}&\frac{b}{\textcolor{red}{c}} \cdot \frac{d}{e} =\frac{\textcolor{blue}{a}\,\cdot\,\textcolor{red}{c}+b}{\textcolor{red}{c}} \cdot \frac{d}{e}$

Weitere Beispiele

$\frac{3}{6}\cdot&\textcolor{blue}{4}\frac{1}{\textcolor{red}{2}}=\frac{3\cdot(\textcolor{blue}{4}\,\cdot&\,\textcolor{red}{2}+1)}{6\cdot&2}=\frac{3\,\cdot&\,9}{6\,\cdot&\,2}=\frac{27\textcolor{teal}{:3}}{12\textcolor{teal}{:3}}=\frac{9}{4}$

$4\frac{2}{5}\cdot&1\frac{3}{6}=\frac{22}{5}\cdot\frac{9}{6}=\frac{198}{30}=\frac{33}{5}$

Brüche kürzen

Durch Kürzen kannst du Brüche vereinfachen. Hierzu müssen Zähler und Nenner einen gemeinsamen Teiler haben. Dabei teilst du den Zähler und den Nenner des Bruchs durch dieselbe Zahl.

$\frac{4}{12} = \frac{4\textcolor{teal}{\,:4}}{12\textcolor{teal}{\,:4}} = \frac{1}{3}$

Vor dem Brüche multiplizieren kürzen

Falls die Brüche große Zahlen beinhalten, ist es häufig sinnvoll schon vor dem Brüche multiplizieren zu kürzen. Damit kannst du dir das Rechnen mit den Brüchen vereinfachen und hast dadurch am Schluss keine riesigen Zahlen im Ergebnis.

$\frac{4\textcolor{teal}{\,:2}}{8\textcolor{teal}{\,:2}} \cdot \frac {5\textcolor{teal}{\,:5}}{15\textcolor{teal}{\,:5}} = \frac{2}{4} \cdot \frac{1}{3}$

Über Kreuz kürzen

Außerdem kannst du beim Brüche multiplizieren auch über Kreuz kürzen. Genauer gesagt, kannst du die Zähler also mit dem gegenüberliegenden Nenner kürzen.

$\frac{\textcolor{blue}{1}}{\textcolor{red}{\not{4}}} \,\cdot\, \frac{\textcolor{blue}{\not{4}}}{\textcolor{red}{8}} = \frac{\textcolor{blue}{1}}{\textcolor{red}{8}}$

Ausführlich anhand vieler Beispiele erklären wir dir das Kürzen in unserem extra Video . Schau es dir gleich an.

Brüche kürzen, Bruch kürzen, Kürzen von Brüchen, kürzen — Zum Video: Brüche kürzen

Mehrere Brüche multiplizieren

im Videozur Stelle im Video springen

(03:04)

Beim Multiplizieren von Brüchen kann es auch vorkommen, dass du mehr als zwei Brüche multiplizieren musst. Dabei gehst du genauso vor wie in den vorherigen Beispielen.

Beispiel

Berechne

$\frac{5}{8} \cdot \frac{3}{2} \cdot \frac{2}{4}.$

1.Brüche multiplizieren: Multipliziere zuerst alle Zähler und alle Nenner miteinander.

$\frac{\textcolor{blue}{5}}{\textcolor{red}{8}}\cdot&\frac{\textcolor{blue}{3}}{\textcolor{red}{2}}\cdot&\frac{\textcolor{blue}{2}}{\textcolor{red}{4}}&=&\frac{\textcolor{blue}{5\,&\cdot&\,3&\,\cdot&\,2}}{\textcolor{red}{8\,\cdot\,2\,\cdot\,4}}$

3.Kürzen: Streiche daraufhin alle Zahlen, die im Zähler und im Nenner vorkommen.

$\frac{5}{8} \cdot \frac{3}{\textcolor{teal}{2}} \cdot \frac{\textcolor{teal}{2}}{4} = \frac{5 \,\cdot\,3\,\cdot\,\textcolor{teal}{\not{2}}}{8\,\cdot\,\textcolor{teal}{\not{2}}\,\cdot\,4}$

3.Ergebnis berechnen

$\frac{5 \,\cdot\,3}{8\,\cdot\,4} = \frac{15}{32}$

Weitere Beispiele

$\frac{1}{2}\cdot\frac{4}{3}\cdot\frac{6}{5}=\frac{24\textcolor{teal}{\,:6}}{30\textcolor{teal}{\,:6}}=\frac{4}{5}$

$\frac{2}{3}\cdot\frac{5}{2}\cdot\frac{3}{8}=\frac{\not{\textcolor{orange}{2}}\,\cdot&\,5\,\cdot&\,\not{\textcolor{teal}{3}}}{\not{\textcolor{teal}{3}}\,\cdot&\,\not{\textcolor{orange}{2}}\,\cdot&\,8}=\frac{5}{8}$

Brüche Multiplizieren Aufgaben

Im Folgenden kannst du das Bruchrechnen mit unseren Aufgaben zur Multiplikation von Brüchen üben und testen, ob du alles verstanden hast.

Aufgabe 1: $\frac{7}{8}\cdot&4=$

Aufgabe 2: $}\frac{11}{4}\cdot\frac{8}{6}=$

Aufgabe 3: $\frac{2}{5}\cdot\frac{6}{10}\cdot&1\frac{3}{4}=$

Lösungen

Nachdem du die Aufgaben bearbeitet hast, kannst du hier überprüfen, ob du zu jeder Aufgabe die richtige Lösung gefunden hast.

Lösung 1

$\frac{\textcolor{blue}{7}}{8}\cdot&\textcolor{red}{4}}&=\frac{\textcolor{blue}{7}\cdot\textcolor{red}{4}}{8}=&\frac{28}{8}&=&\frac{28\textcolor{teal}{:4}}{8\textcolor{teal}{:4}}&=&\frac{7}{2}$

(Brüche multiplizieren mit ganzen Zahlen)

Lösung 2

$}\frac{\textcolor{blue}{11}}{\textcolor{red}{4}}\cdot\frac{\textcolor{blue}{8}}{\textcolor{red}{6}}=\frac{11\,\cdot&\,8}{4\,\cdot&\,6}=\frac{88\,\textcolor{teal}{:8}}{24\,\textcolor{teal}{:8}}=\frac{11}{3}$

(Multiplikation von Brüchen mit Brüchen)

Lösung 3

$\frac{\textcolor{blue}{2}}{\textcolor{red}{5}}\cdot\frac{\textcolor{blue}{6}}{\textcolor{red}{10}}\cdot&\textcolor{blue}{1}\frac{\textcolor{blue}{3}}{\textcolor{red}{4}}=\frac{2\cdot6\cdot(1\cdot4+3)}{5\cdot10\cdot4}=\frac{84}{200}=\frac{21}{50}$

(Mehrere Brüche/Gemischte Brüche multiplizieren)

Brüche multiplizieren — häufigste Fragen

(ausklappen)

Wie multipliziere ich negative Brüche?

Negative Brüche multiplizierst du, indem du zuerst auf die Minuszeichen schaust und dann ganz normal Zähler mal Zähler und Nenner mal Nenner rechnest. Haben beide Faktoren ein Minus, wird das Ergebnis plus. Hat nur einer ein Minus, wird das Ergebnis minus. Zum Beispiel: $-\frac{2}{3}\cdot\frac{5}{4}=-\frac{10}{12}=-\frac{5}{6}$ .
Wie schreibe ich einen unechten Bruch als gemischte Zahl?

Einen unechten Bruch schreibst du als gemischte Zahl, indem du den Zähler durch den Nenner teilst. Die ganze Zahl ist das Ergebnis ohne Rest. Der Rest wird der neue Zähler und der Nenner bleibt gleich. Zum Beispiel: $\frac{17}{5}=17:5=3$ Rest , also $3\frac{2}{5}$ .
Was rechne ich zuerst, wenn in einer Aufgabe mit Brüchen mal und plus vorkommen?

Bei Brüchen mit mal und plus rechnest du zuerst alle Multiplikationen und danach die Additionen. Danach bringst du beim Addieren die Brüche auf einen gleichen Nenner. Zum Beispiel: $\frac{1}{2}+\frac{2}{3}\cdot\frac{3}{4}=\frac{1}{2}+\frac{6}{12}=\frac{1}{2}+\frac{1}{2}=1$ .

Brüche multiplizieren und dividieren

Zum Multiplizieren von Brüchen brauchst du immer zwei Brüche, bei denen du Zähler mal Zähler und Nenner mal Nenner rechnest. Brüche multiplizieren spielt auch beim Dividieren eine wichtige Rolle. Wenn du wissen willst, wofür du die Multiplikation beim Brüche teilen brauchst, schau dir doch unser Video zum Brüche dividieren an.