Video

Quiz

Hier geht's zum Video „Bruchrechnen“

Bruchrechnen Aufgaben

Wichtige Inhalte in diesem Video

Brüche kürzen Aufgaben

Brüche erweitern Aufgaben

Brüche addieren Aufgaben

Brüche subtrahieren Aufgaben

Brüche multiplizieren Aufgaben

Brüche dividieren Aufgaben

Du möchtest Aufgaben zum Bruchrechnen bearbeiten und dir Lösungen zu den Übungen anschauen? Alles zum Brüche üben findest du in diesem Beitrag! Schau dir auch unser Video für eine ausführliche Erklärung der Bruchaufgaben an.

Inhaltsübersicht

Bruchrechnen Aufgaben einfach erklärt

Hier findest du verschiedene Aufgaben zum Bruchrechnen . Dazu zählen:

Kürzen und Erweitern von Brüchen: Beim Kürzen teilst du Zähler und Nenner durch die gleiche Zahl. Im Gegensatz dazu multiplizierst du beim Erweitern beide mit der gleichen Zahl.
$\frac{\textcolor{blue}{1}}{\textcolor{red}{3}} = \frac{\textcolor{blue}{1}\textcolor{teal}{\,\cdot3}}{\textcolor{red}{3}\textcolor{teal}{\,\cdot3}} = \frac{3}{9}$
Addieren und Subtrahieren von Brüchen: Wenn beide Brüche den gleichen Nenner haben, rechnest du einfach Zähler plus/minus Zähler und übernimmst den Nenner.
$\frac{\textcolor{blue}{2}}{\textcolor{red}{5}} +\frac{\textcolor{blue}{1}}{\textcolor{red}{5}} = \frac{\textcolor{blue}{2\,+\,1}}{\textcolor{red}{5}} = \frac{\textcolor{blue}{3}}{\textcolor{red}{5}}$
Bei unterschiedlichen Nennern musst du die Brüche zuerst durch Kürzen oder Erweitern auf einen Nenner bringen.

Multiplizieren von Brüchen: Dabei gilt die Regel Zähler mal Zähler und Nenner mal Nenner.
$\frac{\textcolor{blue}{2}}{\textcolor{red}{4}}\cdot\frac{\textcolor{blue}{3}}{\textcolor{red}{5}} = \frac{\textcolor{blue}{2\,\cdot\,3}}{\textcolor{red}{4\,\cdot\,5}} = \frac{\textcolor{blue}{6}}{\textcolor{red}{20}}$

Dividieren von Brüchen: Hier ermittelst du zuerst den Kehrwert des zweiten Bruchs. Den multiplizierst du dann mit dem ersten Bruch.
$\frac{1}{3} : \frac{\textcolor{blue}{5}}{\textcolor{red}{6}} = \frac{1}{3} \cdot \frac{\textcolor{red}{6}}{\textcolor{blue}{5}} = \frac{1\,\cdot\,\textcolor{red}{6}}{3\,\cdot\,\textcolor{blue}{5}} = \frac{6}{15}$

Schau dir jetzt die Übungen zum Bruchrechnen an! Anschließend kannst du überprüfen, ob du die Bruch Aufgaben verstanden, und alle Aufgaben richtig gelöst hast.

Brüche kürzen Aufgaben

im Videozur Stelle im Video springen

Du kürzt Brüche, indem du Zähler und Nenner jeweils durch die gleiche Zahl teilst. Wende das Brüche kürzen an folgenden Übungen an.

Aufgabe 1: Kürze den Bruch $\frac{6}{8}$ mit 2.

Aufgabe 2: Kürze den Bruch $\frac{9}{21}$ mit 3.

Aufgabe 3: Kürze $\frac{8}{24}$ soweit wie möglich.

Aufgabe 4: Kürze die Brüche $\frac{12}{18}, \frac{15}{30}$ und $\frac{12}{36}$ so, dass sie alle denselben Nenner haben.

Aufgabe 5: Mit welcher Zahl wurde hier gekürzt? $\frac{12}{54} = \frac{2}{9}$

Brüche kürzen Lösung

Lösung 1:

$\frac{6\textcolor{teal}{\,:2}}{8\textcolor{teal}{\,:2}}=\frac{3}{4}$

(Du kürzt den Bruch mit 2, indem du den Zähler 6 und den Nenner 8 durch 2 teilst.)

Lösung 2:

$\frac{9\textcolor{teal}{\,:3}}{21\textcolor{teal}{\,:3}} = \frac{3}{7}$

Lösung 3:

$\frac{8\textcolor{teal}{\,:8}}{24\textcolor{teal}{\,:8}}=\frac{1}{3}$

Lösung 4:

$\frac{12\textcolor{teal}{\,:3}}{18\textcolor{teal}{\,:3}} = \frac{4}{6}\; \; \; \frac{15\textcolor{teal}{\,:5}}{30\textcolor{teal}{\,:5}}=\frac{3}{6} \; \; \; \frac{12\textcolor{teal}{\,:6}}{36\textcolor{teal}{\,:6}} = \frac{2}{6}$

Lösung 5:

$\frac{12\textcolor{teal}{\,:6}}{54\textcolor{teal}{\,:6}} = \frac{2}{9}$

Brüche erweitern Aufgaben

im Videozur Stelle im Video springen

Beim Erweitern von Brüchen werden Zähler und Nenner mit derselben Zahl multipliziert. Löse zum Brüche erweitern folgende Aufgaben.

Aufgabe 1: Erweitere den Bruch $\frac{2}{7}$ mit 3.

Aufgabe 2: Bringe den Bruch $\frac{3}{4}$ auf den Nenner 24.

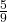Aufgabe 3: Bringe die Brüche $\frac{3}{6}$ und $\frac{5}{9}$ auf denselben Nenner.

Aufgabe 4: Erweitere die Brüche $\frac{2}{3}$ und $\frac{5}{7}$ mit dem Nenner des anderen Bruchs.

Aufgabe 5: Womit wurde der Bruch erweitert? 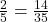$\frac{2}{5} = \frac{14}{35}$ .

Brüche erweitern Lösung

Lösung 1:

$\frac{2\textcolor{teal}{\,\cdot3}}{7\textcolor{teal}{\,\cdot3}} = \frac{6}{21}$

(Multipliziere den Zähler und den Nenner jeweils mit 3.)

Lösung 2:

$\frac{3\textcolor{teal}{\,\cdot6}}{4\textcolor{teal}{\,\cdot6}} = \frac{18}{24}$

Lösung 3:

$\frac{3\textcolor{teal}{\,\cdot3}}{6\textcolor{teal}{\,\cdot3}} = \frac{9}{18} \; \; \; \frac{5\textcolor{teal}{\,\cdot2}}{9\textcolor{teal}{\,\cdot2}}=\frac{10}{18}$

Lösung 4:

$\frac{2\textcolor{teal}{\,\cdot7}}{3\textcolor{teal}{\,\cdot7}} = \frac{14}{21} \; \; \; \frac{5\textcolor{teal}{\,\cdot3}}{7\textcolor{teal}{\,\cdot3}} = \frac{15}{21}$

Lösung 5:

$\frac{2\textcolor{teal}{\,\cdot7}}{5\textcolor{teal}{\,\cdot7}} = \frac{14}{35}$

Brüche addieren Aufgaben

im Videozur Stelle im Video springen

Du kannst Brüche mit gleichen Nennern zusammenzählen, indem du die Zähler addierst. Brüche mit unterschiedlichen Nennern musst du vorher auf einen Nenner bringen. Auch zum Brüche addieren haben wir dir einige Aufgaben erstellt.

Aufgabe 1: Addiere die Gleichnamigen Brüche.

$\frac{5}{14}+\frac{4}{14}$

Aufgabe 2: Addiere die Ungleichnamigen Brüche.

$\frac{1}{3} + \frac{3}{5}$

Aufgabe 3: Addiere die gemischte Zahl mit dem Bruch.

$2\frac{7}{5} + \frac{1}{5}$

Aufgabe 4: Addiere die ganze Zahl mit dem Bruch.

$3+\frac{2}{6}$

Aufgabe 5: Addiere den Bruch mit der gemischten Zahl.

$\frac{1}{4} + 5\frac{2}{8}$

Brüche addieren Lösung

Lösung 1:

$\frac{\textcolor{blue}{5}}{\textcolor{red}{14}}+\frac{\textcolor{blue}{4}}{\textcolor{red}{14}} = \frac{\textcolor{blue}{5\,+\,4}}{\textcolor{red}{14}}= \frac{9}{\textcolor{red}{14}}$

(Zähle die beiden Nenner 5 und 4 zusammen und übernimm den Nenner 14)

Lösung 2:

$\frac{1}{3} + \frac{3}{5} = \frac{1\textcolor{teal}{\,\cdot5}}{3\textcolor{teal}{\,\cdot5}}+\frac{3\textcolor{teal}{\,\cdot3}}{5\textcolor{teal}{\,\cdot3}} = \frac{5}{15} + \frac{9}{15} = \frac{14}{15}$

Lösung 3:

$\textcolor{orange}{2}\frac{7}{\textcolor{red}{5}} + \frac{1}{5} = \frac{\textcolor{orange}{2}\,\cdot\textcolor{red}{5}\,+7}{\textcolor{red}{5}} +\frac{1}{5} = \frac{17}{5} + \frac{1}{5}= \frac{18}{5} = 3\frac{3}{5}$

Lösung 4:

$\textcolor{orange}{3}+\frac{2}{6}=\frac{\textcolor{orange}{3}}{1}+\frac{2}{6} =\frac{3\textcolor{teal}{\,\cdot6}}{1\textcolor{teal}{\,\cdot6}} +\frac{2}{6} = \frac{18}{6}+\frac{2}{6} = \frac{20}{6} = 3\frac{2}{6} = 3\frac{1}{3}$

Lösung 5:

$\frac{1}{4} + \textcolor{orange}{5}\frac{2}{\textcolor{red}{8}}=\frac{1}{4} + \frac{\textcolor{orange}{5}\,\cdot\,\textcolor{red}{8}\,+\,2}{\textcolor{red}{8}}=\frac{1}{4}+\frac{42\textcolor{teal}{\,:2}}{8\textcolor{teal}{\,:2}} = \frac{1}{4} + \frac{21}{4} = \frac{22}{4} = 5\frac{1}{2}$

Brüche subtrahieren Aufgaben

im Videozur Stelle im Video springen

Beim Subtrahieren brauchst du, genauso wie beim Addieren, Brüche mit gleichen Nennern. Ungleichnamige Brüche musst du vorher umwandeln. Zum Brüche subtrahieren rechnest du am besten folgende Übungen durch.

Aufgabe 1: Löse folgende Subtraktion

$\frac{5}{8} - \frac{3}{8}$

Aufgabe 2: Berechne die Subtraktion.

$\frac{8}{12} - \frac{1}{3}$

Aufgabe 3: Ziehe den Bruch von dem gemischten Bruch ab.

$2\frac{1}{6} - \frac{4}{6}$

Aufgabe 4: Ziehe den Bruch vom gemischten Bruch ab.

$1\frac{2}{8} - \frac{3}{4}$

Aufgabe 5: Ziehe den Bruch von der ganzen Zahl ab.

$1 - \frac{7}{13}$

Brüche subtrahieren Lösung

Lösung 1:

$\frac{\textcolor{blue}{5}}{\textcolor{red}{8}} - \frac{\textcolor{blue}{3}}{\textcolor{red}{8}} = \frac{\textcolor{blue}{5-3}}{\textcolor{red}{8}}=\frac{2\textcolor{teal}{\,:2}}{8\textcolor{teal}{\,:2}} = \frac{1}{4}$

(Ziehe den zweiten Zähler 3 vom ersten Zähler 5 ab und übernimm den Nenner 8)

Lösung 2:

$\frac{8}{12}-\frac{1}{3}=\frac{8\textcolor{teal}{\,:4}}{12\textcolor{teal}{\,:4}} - \frac{1}{3} = \frac{2}{3}-\frac{1}{3} = \frac{2-1}{3} = \frac{1}{3}$

Lösung 3:

$\textcolor{orange}{2}\frac{1}{\textcolor{red}{6}} - \frac{4}{6} = \frac{\textcolor{orange}{2}\,\cdot\,\textcolor{red}{6}\,+1}{\textcolor{red}{6}}-\frac{4}{6}=\frac{13}{6}-\frac{4}{6} = \frac{9}{6} = 1\frac{1}{2}$

Lösung 4:

$\textcolor{orange}{1}\frac{2}{\textcolor{red}{8}} - \frac{3}{4}=\frac{\textcolor{orange}{1}\,\cdot\textcolor{red}{8}\,+2}{\textcolor{red}{8}} - \frac{3}{4}= \frac{10\textcolor{teal}{\,:2}}{8\textcolor{teal}{\,:2}} -\frac{3}{4} = \frac{5}{4} - \frac{3}{4} =\frac{2\textcolor{teal}{\,:2}}{4\textcolor{teal}{\,:2}}= \frac{1}{2}$

Lösung 5:

$\textcolor{orange}{1} - \frac{7}{13} = \frac{\textcolor{orange}{1}\textcolor{teal}{\,\cdot13}}{1\textcolor{teal}{\,\cdot13}}-\frac{7}{13} = \frac{13}{13}-\frac{7}{13} = \frac{6}{13}$

Brüche multiplizieren Aufgaben

im Videozur Stelle im Video springen

Das Multiplizieren von Brüchen ist ganz einfach. Dabei rechnest du Zähler mal Zähler und Nenner mal Nenner. Auch zum Brüche multiplizieren haben wir einige Aufgaben zum Bruchrechnen für dich vorbereitet.

Aufgabe 1: Multipliziere die Brüche.

$\frac{4}{6}\cdot\frac{3}{7}$

Aufgabe 2: Löse die Multiplikation.

$\frac{6}{22}\cdot\frac{9}{3}$

Aufgabe 3: Multipliziere die ganze Zahl mit dem Bruch.

$3\cdot\frac{2}{17}$

Aufgabe 4: Berechne die Multiplikation mit einem gemischten Bruch.

$\frac{1}{3}\cdot2\frac{2}{9}$

Aufgabe 5: Multipliziere die gemischten Brüche.

$1\frac{7}{5} \cdot 3\frac{1}{8}$

Brüche multiplizieren Lösung

Lösung 1:

$\frac{\textcolor{blue}{4}}{\textcolor{red}{6}}\cdot\frac{\textcolor{blue}{3}}{\textcolor{red}{7}} = \frac{\textcolor{blue}{4\,\cdot\,3}}{\textcolor{red}{6\,\cdot\,7}}=\frac{12\textcolor{teal}{\,:6}}{42\textcolor{teal}{\,:6}} =\frac{2}{7}$

(Multipliziere die Zähler 4 ⋅ 3 = 12 und die Nenner 6 ⋅ 7 = 42 und kürze das Ergebnis)

Lösung 2:

$\frac{6}{22}\cdot\frac{9}{3} = \frac{6\,\cdot\,9}{22\,\cdot\,3} = \frac{54\textcolor{teal}{\,:6}}{66\textcolor{teal}{\,:6}} = \frac{9}{11}$

Lösung 3:

$\textcolor{blue}{3}\cdot\frac{2}{17} =\frac{\textcolor{blue}{3}}{1} \cdot\frac{2}{17}= \frac{\textcolor{blue}{3}\,\cdot\,2}{17}= \frac{6}{17}$

Lösung 4:

$\frac{1}{3}\cdot\textcolor{orange}{2}\frac{2}{\textcolor{red}{9}} = \frac{1}{3} \cdot \frac{\textcolor{orange}{2}\,\cdot\,\textcolor{red}{9}+2}{9}= \frac{1}{3} \cdot \frac{20}{9} = \frac{1\,\cdot\,20}{3\,\cdot\,9} = \frac{20}{27}$

Lösung 5:

$\textcolor{orange}{1}\frac{7}{\textcolor{red}{5}} \cdot \textcolor{orange}{3}\frac{1}{\textcolor{red}{8}} = \frac{\textcolor{orange}{1}\,\cdot\,\textcolor{red}{5}+7}{\textcolor{red}{5}} \cdot \frac{\textcolor{orange}{3}\,\cdot\,\textcolor{red}{8}+1}{\textcolor{red}{8}} = \frac{12}{5}\cdot\frac{25}{8} = \frac{12\cdot25}{5\,\cdot\,8} = \frac{300}{40} = \frac{15}{2} = 7\frac{1}{2}$

Brüche dividieren Aufgaben

im Videozur Stelle im Video springen

Die Multiplikation von Brüchen brauchst du auch bei der Division. Hier wird der Kehrwert des zweiten Bruchs mit dem ersten Bruch multiplizierst. Löse folgende Aufgaben zur Bruchrechnung.

Aufgabe 1:

$\frac{5}{8}:\frac{2}{3}$

Aufgabe 2:

$\frac{7}{26}:\frac{5}{13}$

Aufgabe 3:

$\frac{4}{7}:6$

Aufgabe 4:

$-\frac{4}{16}:-\frac{3}{7}$

Aufgabe 5:

$3\frac{1}{2}:\frac{5}{3}$

Brüche dividieren Lösung

Lösung 1:

$\frac{5}{8}:\frac{\textcolor{blue}{2}}{\textcolor{red}{3}} = \frac{5}{8} \cdot \frac{\textcolor{red}{3}}{\textcolor{blue}{2}} = \frac{5\,\cdot\,\textcolor{red}{3}}{8\,\cdot\,\textcolor{blue}{2}} = \frac{15}{16}$

(Vertausche den Zähler 2 und den Nenner 3 im zweiten Bruch (Kehrwert) und multipliziere ihn mit dem ersten Bruch $\frac{5}{8}$ )

Lösung 2:

$\frac{7}{26}:\frac{\textcolor{blue}{5}}{\textcolor{red}{13}} = \frac{7}{26} \cdot\frac{\textcolor{red}{13}}{\textcolor{blue}{5}} = \frac{7\,\cdot\,\textcolor{red}{13}}{26\,\cdot\,\textcolor{blue}{5}} = \frac{91\textcolor{teal}{\,:13}}{130\textcolor{teal}{\,:13}} = \frac{7}{10}$

Lösung 3:

$\frac{4}{7}:\textcolor{blue}{6} = \frac{4}{7} : \frac{\textcolor{blue}{6}}{\textcolor{red}{1}} = \frac{4}{7}\cdot\frac{\textcolor{red}{1}}{\textcolor{blue}{6}} = \frac{4\,\cdot\,\textcolor{red}{1}}{7\cdot \textcolor{blue}{6}} = \frac{4\textcolor{teal}{\,:2}}{42\textcolor{teal}{\,:2}} = \frac{2}{21}$

Lösung 4:

$-(\frac{4}{16}):-(\frac{\textcolor{blue}{3}}{\textcolor{red}{7}}) = -(\frac{4}{16}):-(\frac{\textcolor{red}{7}}{\textcolor{blue}{3}})= \frac{(-4)\,\cdot\,(-\textcolor{red}{7})}{16\,\cdot\,\textcolor{blue}{3}}= \frac{28\textcolor{teal}{\,:4}}{48\textcolor{teal}{\,:4}}=\frac{7}{12}$

Lösung 5:

$\textcolor{orange}{3}\frac{1}{\textcolor{red}{2}}:\frac{5}{3} = \frac{\textcolor{orange}{3}\,\cdot\,\textcolor{red}{2}+1}{\textcolor{red}{2}} : \frac{5}{3} = \frac{7}{2} : \frac{\textcolor{blue}{5}}{\textcolor{red}{3}} = \frac{7}{2}\cdot\frac{\textcolor{red}{3}}{\textcolor{blue}{5}} = \frac{7\,\cdot\,\textcolor{red}{3}} {2\,\cdot\,\textcolor{blue}{5}} = \frac{21}{10} = 2\frac{1}{10}$

Nachdem du alle Übungen zum Bruchrechnen erledigt hast, bist du jetzt super auf den nächsten Test vorbereitet.

Quiz zum Thema Bruchrechnen Aufgaben

Zusammenfassung Bruchrechnen Aufgaben

Nach den Aufgaben zur Bruchrechnung kannst du dir zur Wiederholung unsere Videos zu den verschiedenen Rechenarten noch einmal anschauen.

Beim Kürzen werden Zähler und Nenner des Bruchs durch die gleiche Zahl geteilt.
Beim Erweitern werden Zähler und Nenner des Bruchs mit der gleichen Zahl multipliziert.
Beim Addieren von Brüchen mit gleichen Nennern zählst du nur die Zähler zusammen. Ungleichnamige Brüche musst du vorher auf einen Nenner bringen.
Beim Subtrahieren von Brüchen mit gleichen Nennern rechnest du Zähler minus Zähler. Ungleichnamige Brüche musst du auch beim Minus rechnen auf einen Nenner bringen.
Beim Multiplizieren von Brüchen gilt die Regel Zähler mal Zähler und Nenner mal Nenner.
Beim Dividieren von Brüchen berechnest du den Kehrwert des zweiten Bruchs und multiplizierst ihn mit dem ersten Bruch.

Brüche dividieren — zum Video: Brüche dividieren

zur Videoseite: Bruchrechnen Aufgaben

Beliebte Inhalte aus dem Bereich Mathematische Grundlagen

Bruchrechnen Aufgaben

Brüche gleichnamig machen

Brüche vergleichen und ordnen

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .