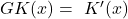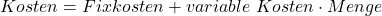Kostenfunktion
In diesem Artikel wird dir die Kostenfunktion nähergebracht. Zuerst erklären wir dir die Formel zur Kostenfunktion. Anschließend wenden wir die Formel anhand von einem Beispiel an.
Schritt für Schritt lernst du die Kostenfunktion in unserem Lernvideo kennen.
Inhaltsübersicht
Kostenfunktion Definition
Die Kostenfunktion, auch Gesamtkostenfunktion oder Totalkostenfunktion genannt, beschreibt den Zusammenhang zwischen Produktionsmenge und den dazugehörigen Kosten. Sie ist eine Formel aus dem Rechnungswesen und lässt sich u.a. in lineare, degressive und progressive Kostenfunktionen unterteilen.
Kostenfunktion aufstellen
Die Kostenfunktion gibt die Kosten an, welche bei einer produzierten Menge x eines bestimmten Gutes anfallen. Es wird zwischen zwei verschiedenen Kostenarten unterschieden, fixe und variable Kosten :
Fixkosten : unabhängig von der produzierten Menge, fallen immer in gleicher Höhe an (z.B. Miete für Gebäude, Anschaffungskosten für Maschinen, Gehalt des Geschäftsführers)
Variable Kosten : abhängig von der produzierten Menge, Höhe der variablen Kosten variiert (z.B. Rohstoffe, Betriebsstoffe, Fertigungslöhne)
Mit den beiden Kostenarten und der Menge lässt sich die Kostenfunktion aufstellen.
Kostenfunktion berechnen
Ziel ist es also, eine Funktion aufzustellen, die die Gesamtkosten unseres Unternehmens darstellt. Haben wir diese ermittelt, müssen wir letztendlich nur noch unsere Produktionsmengen einsetzen, um die jeweiligen Kosten zu erhalten.
Wie das funktioniert wird im Folgenden an einem Beispiel veranschaulicht.
Kostenfunktion Beispiel lineare Kostenfunktion
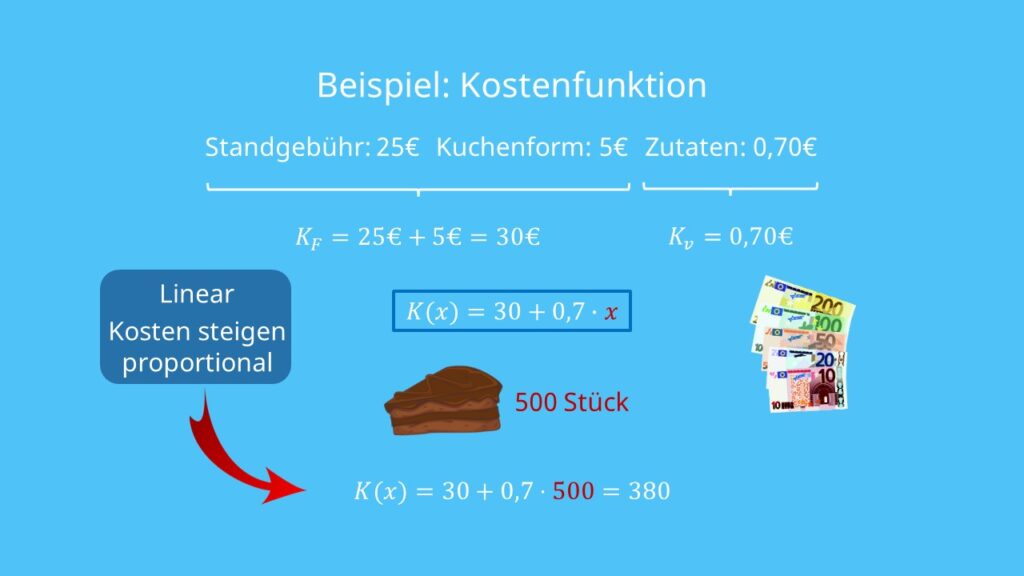
Um dein Studentengehalt ein bisschen zu verbessern, möchtest du auf dem Uni-Sommerfest Kuchen verkaufen. Die Standgebühren betragen 25€, außerdem brauchst du noch eine neue Kuchenform, die du für 5€ im Supermarkt besorgst. Für die Zutaten (Zucker, Mehl, Milch, Eier) gibst du insgesamt 75€ aus und kannst damit 25 Kuchen backen, die du jeweils in sechs Stücke teilst.
Berechnung der Fixkosten
Um die Fixkosten zu erhalten, addieren wir die Standgebühr und die Kosten für die Kuchenform:
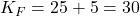
Berechnung der variablen Kosten
Die variablen Kosten erweisen sich als ein bisschen komplizierter. Da du insgesamt 25 Kuchen bäckst, die du in sechs Stücke teilst, hast du 25 mal 6 Stücke:
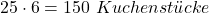
Nun teilen wir die die Kosten für deine Zutaten durch die Anzahl der Kuchenstücke und erhalten die variablen Kosten pro produziertem Kuchenstück:
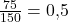
Für die Produktion eines Kuchenstücks hast du demnach variable Kosten i.H.v. 50ct.
Aufstellen der linearen Kostenfunktion
Da wir die variablen und fixen Kosten jetzt kennen, können wir die Kostenfunktion aufstellen. Es gilt also:
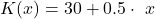
Der Veranstalter des Sommerfests meint nun, dass du mindestens 500 Kuchenstücke brauchst, um den Bedarf der vielen Besucher des Sommerfests zu decken. Du musst also erneut in den Supermarkt und neue Zutaten besorgen. Da wir die Kostenfunktion bereits aufgestellt haben, müsst du die neue Menge (500 Stück) nur noch in die Gleichung einsetzen, um die neuen Kosten zu erhalten.
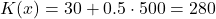
Diese betragen nun 280 €.
Durchschnittskosten und Grenzkosten
Neben den Gesamtkosten interessieren uns auch die Durchschnittskosten bzw. Stückkosten und Grenzkosten.
Durchschnittskosten geben die fixen und variablen Kosten pro produzierter Einheit an. Du erhältst sie einfach, indem du die Kostenfunktion durch x teilst.
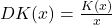
Die Grenzkosten (auch Marginalkosten) hingegen geben die Kosten an, die durch die Produktion einer zusätzlichen Einheit entstehen. Sie interessieren uns, da die Durchschnittskosten bei unterschiedlichen Produktionsmengen bei den meisten Kostenfunktionsarten nicht konstant sind. Es scheint also meist eine Produktionsmenge zu geben, bei welcher die Durchschnittskosten am geringsten sind. Diese liegt dort, wo die Grenzkosten die Durchschnittkosten schneiden. Die Grenzkosten berechnest du durch ableiten der Kostenfunktion.
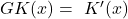
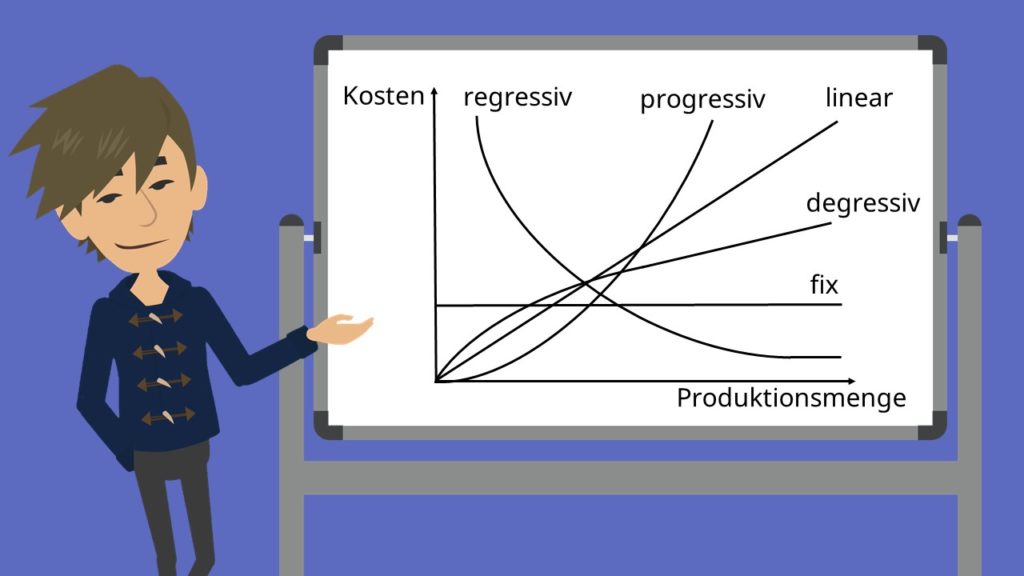
Lineare Kostenfunktion
Wir unterscheiden zwischen vier verschiedenen Kostenfunktionen. Der linearen, der degressiven, der progressiven und der regressiven Kostenfunktion. Je nachdem, welche Funktion gegeben ist, verhalten sich Gesamtkosten, Durchschnittskosten und Grenzkosten verschieden. Beachte immer, dass die variablen Kosten den Verlauf unserer Kostenfunktion bestimmen. Die Fixkosten bestimmen nur unseren y-Achsenabschnitt.
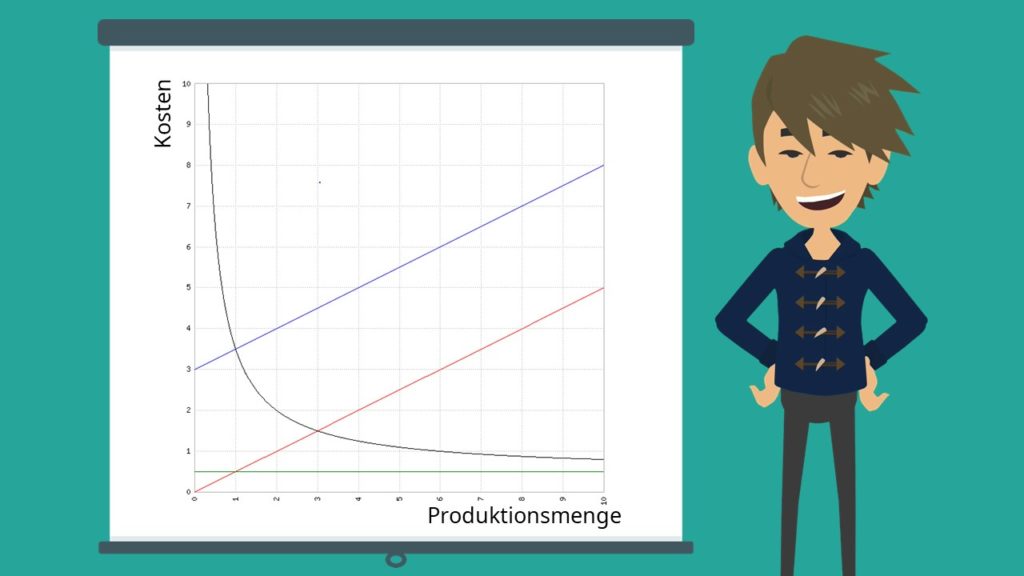
Bei der linearen Kostenfunktion steigen die variablen Kosten proportional zur produzierten Menge an. Die Durchschnittskosten sinken mit steigender Produktion, da die Fixkosten auf eine immer größere Menge verteilt werden. Die Grenzkosten entsprechen den variablen Durchschnittskosten und sind konstant.
Beispiel für lineare Kostenfunktion:
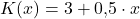
- Blau = Kostenfunktion
- Rot = variable Kosten
- Grün = Durchschnittliche variable Kosten = Grenzkosten
- Schwarz = Durchschnittskosten
Degressive Kostenfunktion
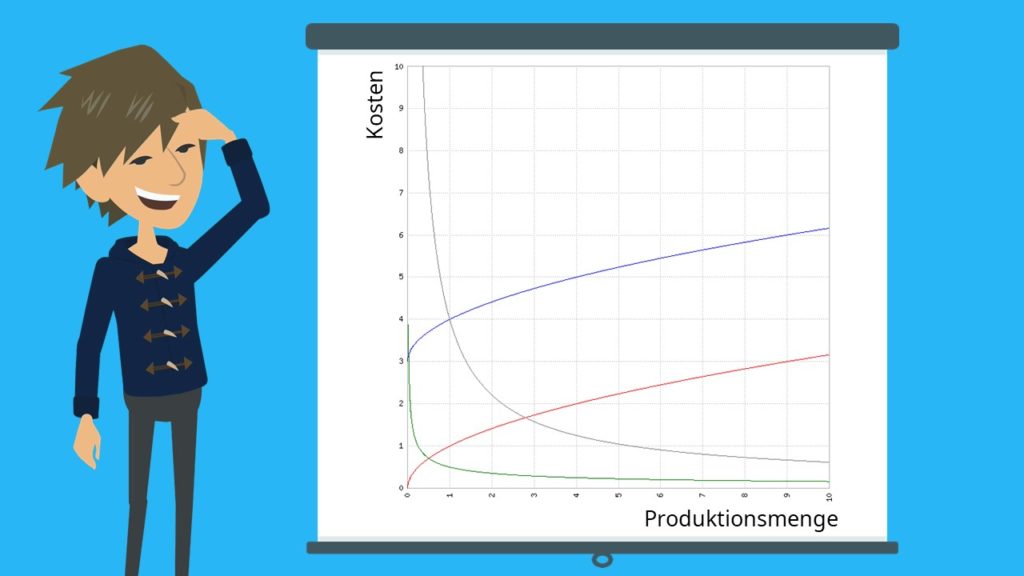
Die degressive Kostenfunktion verhält sich unterproportional. Das heißt, die Kosten nehmen mit steigender Produktion immer langsamer zu. Die Grenzkosten sind damit fallend. Auch die durchschnittlichen Kosten und die durchschnittlichen Variablen Kosten fallen. In der Realität kommt das beispielsweise durch die Gewährung von Mengenrabatten zustande.
Beispiel für degressive Kostenfunktion:
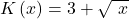
- Blau = Kostenfunktion
- Rot = variable Kosten
- Grün = Grenzkosten
- Schwarz = Durchschnittskosten
Progressive Kostenfunktion
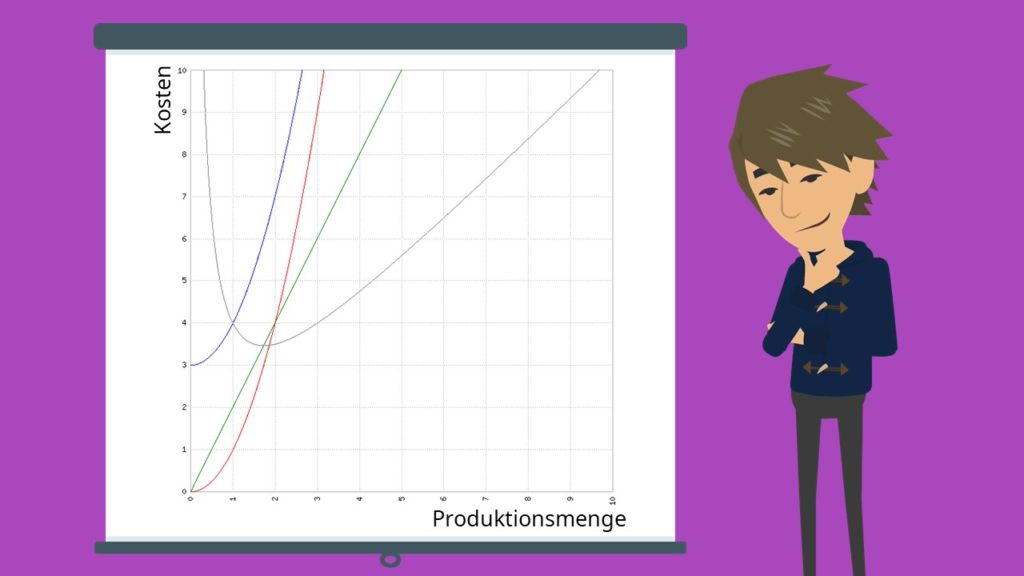
Die progressive Kostenfunktion entspricht der, an der Winkelhalbierenden gespiegelten, degressiven Kostenfunktion. Sie impliziert, dass bei einer Erhöhung der Produktion die variablen Kosten überproportional steigen. Die Grenzkosten steigen monoton, während die Durchschnittskosten erst fallen und dann wieder steigen. Beispielsweise können Überstunden die Kosten von mehr Gütern überdurchschnittlich in die Höhe treiben und somit zu einer progressiven Kostenfunktion führen.
Beispiel für progressive Kostenfunktion:
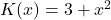
- Blau = Kostenfunktion
- Rot = variable Kosten
- Grün = Grenzkosten
- Schwarz = Durchschnittskosten
Regressive Kostenfunktion
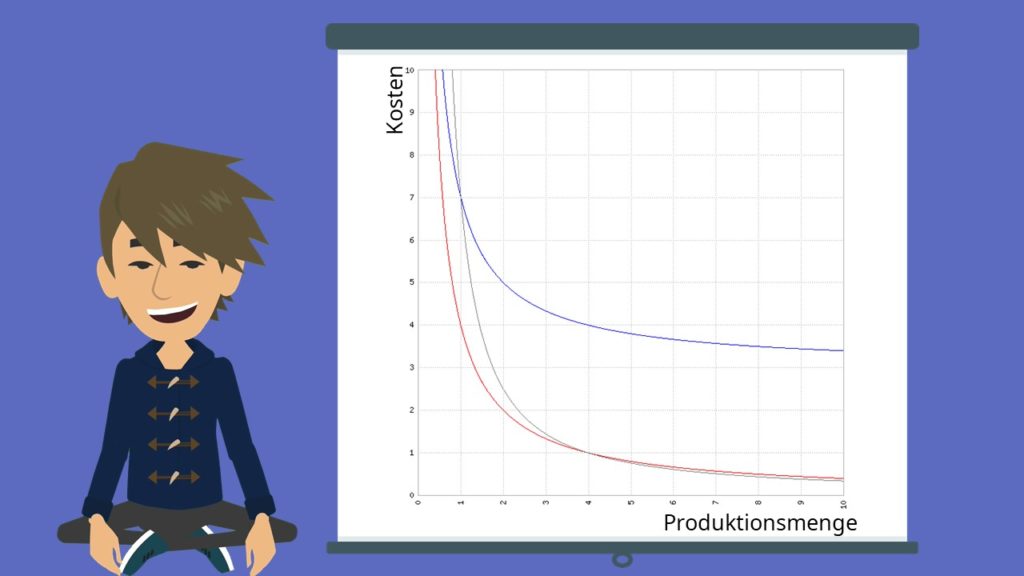
Bei der regressiven Kostenfunktion nehmen die Kosten bei steigender Produktion ab. Damit sinken logischerweise auch die Grenzkosten und die Durchschnittskosten. Regressive Kostenfunktionen treten unter anderem bei Heizkosten in Unternehmen bei steigender Mitarbeiterzahl auf.
Beispiel regressive Kostenfunktion:
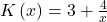
- Blau = Kostenfunktion
- Rot = variable Kosten
- Grün = Grenzkosten
- Schwarz = Durchschnittskosten
Gewinnfunktion und Erlösfunktion
Neben den Kosten zählen Gewinne und Erlöse zu den wichtigsten Kennzahlen in der BWL. Um den Gewinn zu berechnen, ermittelst du mit der Kostenfunktion zuerst die Kosten deines Unternehmens. Außerdem musst du mit der Erlösfunktion den Erlös bestimmen. Wenn du jetzt wissen willst, wie du den Erlös deines Unternehmens berechnest und daraus dann den Gewinn ableitest, schau dir jetzt unseren Beitrag zum Thema Gewinnfunktion und Erlösfunktion an.
Kostenfunktion Zusammenfassung
Du kennst nun die Kostenfunktion und ihre verschiedenen Formen: linear, degressiv, progressiv, regressiv und fix. Außerdem weißt du, wie die allgemeine Formel der Kostenfunktion aussieht 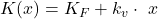 und kannst sie im Rahmen einer Aufgabenstellung ermitteln.
und kannst sie im Rahmen einer Aufgabenstellung ermitteln.
Durchschnittskosten und Grenzkosten kannst du ebenfalls berechnen:
Durchschnittskosten: 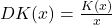
Grenzkosten: