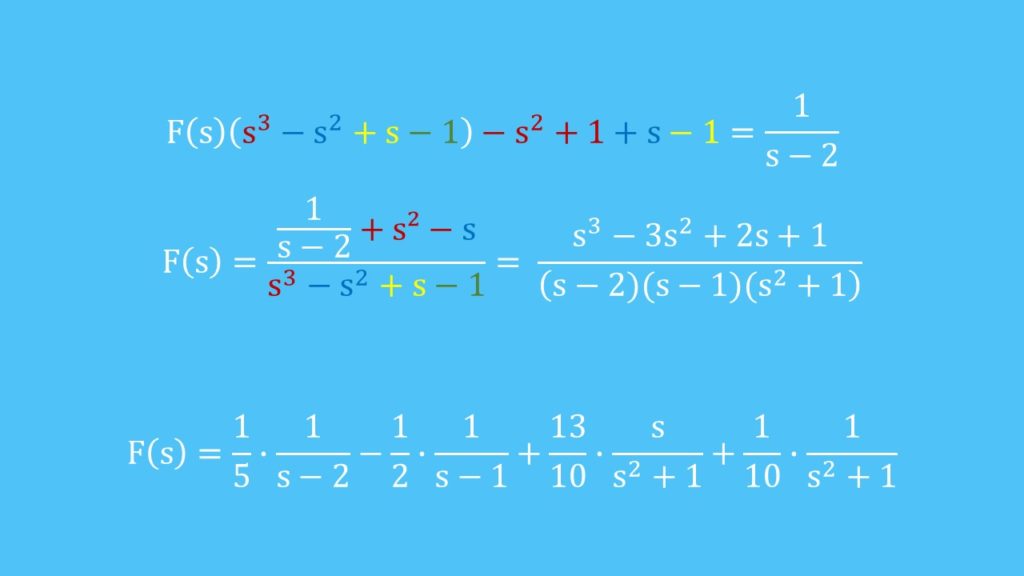Laplace-Transformation
In diesem Beitrag lernst du Schritt für Schritt wie du mithilfe der Laplace Transformation Differentialgleichungen lösen kannst.
Inhaltsübersicht
Was ist die Laplace-Transformation?
In der Regelungstechnik werden Differentialgleichungen verwendet um die Ausgangsgröße eines Systems zu erhalten, wenn die Eingangsgröße bekannt ist. Da es meistens schwierig ist diese Gleichungen mathematisch zu lösen, hilft uns dabei die Laplace-Transformation. Mithilfe ihrer Korrespondenzen ermöglicht sie es, Gleichungen algebraisch zu lösen. Eine Zeitfunktion f(t) wird in eine Bildfunktion F(s) übertragen. Das Laplace-Integral kannst du so definieren:
t ist die Integrationsvariable und s eine komplexe Variable, die sich aus Sigma, Jot und Omega zusammensetzt. Für dieses Übertragen gibt es eine Korrespondenztabelle zur Laplace-Transformation. Auf der einen Seite steht die Originalfunktion im Zeitbereich f(t) und auf der anderen die Laplace-Transformierte F(s) im Bildbereich. Diese Laplace-Tabelle enthält auch die Sätze oder Rechenregeln für die Laplace-Transformation. Die geläufigsten Übertragungen findest du in deinem Übungsbuch oder im Internet!
Laplace-Transformation Beispiel
Wir wollen als Beispiel folgendes Problem mit den Anfangsbedingungen:
im Zeitbereich lösen. Diese Gleichung ist unser f(t).
Jetzt wenden wir das Laplace-Integral auf unser Beispiel an. Für die erste Ableitung erhalten wir  , für die Zweite ergibt sich
, für die Zweite ergibt sich  und für die dritte Ableitung
und für die dritte Ableitung  .
.
Mit der Laplace-Transformation für aus unserem anfänglichen Problem erhalten wir jetzt die transformierte Gleichung:
und lösen nach F(s) auf:
Jetzt haben wir erfolgreich in den Bildbereich transformiert. Um wieder zurück in den Zeitbereich zu gelangen, müssen wir noch weiter umformen. Dazu wenden wir das Verfahren der Partialbruchzerlegung an. Die Idee dahinter ist, die Bildfunktion aus einem Bruch von Polynomen in eine Summe von Teilbrüchen zu zerlegen, die sich anschließend leichter zurücktransformieren lassen. Da diese Umformung sehr kompliziert ist, zeigen wir dir direkt das Ergebnis:
Es folgt der letzte Schritt: Das Rücktransformieren der Bildfunktion in den Zeitbereich. Auch das ist über ein Integral definiert, das wir inverses Transformationsintegral nennen:
Wenden wir es an, erhalten wir für unsere Differentialgleichung f(t) die gesuchte Lösung im Zeitbereich! Dazu transformierst du mit  wieder zurück und nimmst deine Korrespondenztabelle zur Hand! Jetzt haben wir unser Ergebnis:
wieder zurück und nimmst deine Korrespondenztabelle zur Hand! Jetzt haben wir unser Ergebnis:
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Laplace-Transformation – Bildbereich und Zeitbereich
Statt unsere Differentialgleichung umständlich durch Integration im Zeitbereich zu lösen, sind wir einen Umweg über den Bildbereich gegangen, der uns mit Hilfe der Korrespondenzen eine Lösung für den Zeitbereich liefert! Der große Vorteil liegt darin, dass man die charakteristischen Anteile der Funktionen von Übertragungsgliedern in diese Schreibweise integrieren kann. Die Differentialgleichung zur Beschreibung eines Systems lässt sich also durch die Laplace-Transformation für unterschiedliche Eingangsgrößen lösen. Falls du bei der ganzen Umformung nicht mitgekommen bist, zeigen wir dir hier nochmal eine anschauliche Übersicht der kompletten Transformation: