Video

Quiz

Hier geht's zum Video „PID Regler“

Hier geht's zum Video „Blockschaltbild“

Hier geht's zum Video „Regelkreis“

Hier geht's zum Video „Regelstrecke“

P Regler

Wichtige Inhalte in diesem Video

P Regler Erklärung

Regelabweichung eines P Reglers

In diesem Artikel beschäftigen wir uns mit den Grundlagen des P Reglers. Dabei möchten wir dir seine Übertragungsfunktion erklären und vor allem auf die Regelabweichung eingehen. Außerdem zeigen wir, wie das Bodediagramm für den P Regler aussieht und was es aussagt.

Ist dir das zu viel Text? Kein Problem, schau dir einfach unser Video zum P Regler an!

Inhaltsübersicht

P Regler Erklärung

im Videozur Stelle im Video springen

Der P Regler besteht aus einem P Glied und weist damit auch identische Eigenschaften dazu auf. Die Stellgröße ist entsprechend proportional zur Regeldifferenz.

Merke

Bei dem P Regler handelt es sich um einen stätigen Regler mit bleibender Regeldifferenz.

Mathematisch lässt sich dieser Zusammenhang im Zeitbereich wie folgt darstellen:

$y(t)=K_p\cdot e(t)$

y(t) beschreibt hier die Stellgröße und e(t) die Regeldifferenz, also die Differenz des Sollwerts der Regelgröße und ihrem Istwert.

K_P wird als Proportionalitätsfaktor bezeichnet. Er gibt an wie stark die Regeldifferenz verstärkt wird. Je größer der Proportionalitätsfaktor desto geringer die Regeldifferenz. Auf diesen Zusammenhang wird weiter unten genauer eingegangen.

Mit Hilfe der Laplacetransformation lässt sich daraus die Übertragungsfunktion bilden:

$G_{P-Regler}(s)=\frac{Y(s)}{E(s)}=K_P$

Regelabweichung eines P Reglers

im Videozur Stelle im Video springen

Allgemein ist es das Ziel einer Regelung, dass Sollwert und Istwert der Regelgröße übereinstimmen. Ist dies nicht der Fall so gibt es eine Regelabweichung ungleich 0. Bei einem P Regler existiert in der Regel eine bleibende Regelabweichung. Dies lässt sich wie folgt zeigen:

Bleibende Regelabweichung Gesamtübertragungsfunktion P Regler — Bleibende Regelabweichung

In diesem Fall wird ein geschlossener Regelkreis mit einer Rückführung gleich 1 (Rückkopplungszweig) betrachtet. Die Übertragungsfunktion für diesen Regelkreis ergibt sich als:

$\frac{X(s)}{W(s)}=\frac{G_{Regler}(s)\cdot G_{Strecke}(s)}{1+G_{Regler}(s)\cdot G_{Strecke}(s)}$

Die Regelgröße X(s) im Bildbereich ergibt sich damit durch Multiplikation der Gleichung mit der Führungsgröße W(s) .

$X(s)=\frac{G_{Regler}(s)\cdot G_{Strecke}(s)}{1+G_{Regler}(s)\cdot G_{Strecke}(s)}\cdot W(s)$

Außerdem ist bekannt, dass die Regeldifferenz E(s) der Differenz aus dem Sollwert, also der Führungsgröße W(s) und dem Istwert, also der Regelgröße X(s) entspricht.

E(s)=W(s)-X(s)

Setzten wir die oben erhaltene Gleichung für X(s) ein, so erhalten wir:

$E(s)=W(s)-\frac{G_{Regler}(s)\cdot G_{Strecke}(s)\cdot W(s)}{1+G_{Regler}(s)\cdot G_{Strecke}(s)}$

Nun wird dieser Ausdruck noch etwas vereinfacht, indem er als Bruch geschrieben wird:

$E(s)=\frac{{W(s)+G_{Regler}(s)\cdot G_{Strecke}(s)\cdot W(s)-G}_{Regler}(s)\cdot G_{Strecke}(s)\cdot W(s)}{1+G_{Regler}(s)\cdot G_{Strecke}(s)}$

Jetzt wird der Zähler noch vereinfacht. Für die Regeldifferenz ergibt sich:

$E(s)=\frac{W(s)}{1+G_{Regler}(s)\cdot G_{Strecke}(s)}$

Die Regelabweichung e entspricht der Regeldifferenz im eingeschwungenen Zustand, also für 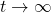$t\rightarrow\infty$ . Im Bildbereich heißt das $s\rightarrow0$ . Mit dem Grenzwertsatz der Laplacetransformation ergibt sich:

$e=\lim\below{s\rightarrow0}{\frac{s\cdot W(s)}{1+G_{Regler}(s)\cdot G_{Strecke}(s)}}$

Beispielsweise wird nun die Führungsgröße W(s) als Einheitssprung (entspricht im Bildbereich $\frac{1}{s}$ ) und die Reglerübertragungsfunktion als K_P , also die eines P-Reglers gewählt.

$e=\lim\below{s\rightarrow0}{\frac{s\cdot\frac{1}{s}}{1+K_P\cdot G_{Strecke}\left(s\right)}=} e=\lim\below{s\rightarrow0}{\frac{1}{1+K_P\cdot G_{Strecke}(s)}}$

Da für diesen Fall nur G_Strecke(s) von s abhängig ist, lässt sich die Gleichung wie folgt umschreiben:

$e=\frac{1}{1+K_P\cdot{\lim\below{s\rightarrow0}\ \ G}_{Strecke}(s)}$

Die Regelabweichung kann für diesen Fall also nur 0 werden, wenn der Grenzwert der Übertragungsfunktion für s gegen 0, gegen unendlich geht. Dies ist nur der Fall, wenn die Regelstrecke mindestens einen reinen Integrator (I-Glied) enthält. Ist der Grenzwert ungleich unendlich, ist eine bleibende Regelabweichung unvermeidlich, kann aber, wie aus oberer Gleichung hervorgeht, durch Erhöhung von K_P reduziert werden.

Bodediagramm des P Reglers

Aus dem Bodediagramm des P Reglers geht hervor, dass er nicht geeignet ist um die Phase eines Systems zu verschieben. Es ist mit ihm allerdings möglich die Amplitude, um K_P anzuheben.

Eigenschaften des P Reglers

Bei Regelstrecken mit Ausgleich (Strecken ohne I-Glied) ergibt sich eine bleibende Regelabweichung, das heißt Soll -und Istwert stimmen nicht überein.
Die Regelabweichung kann durch Erhöhung des Proportionalitätsfaktors verkleinert werden
Der P-Regler ist die einfachste Form des PID-Reglers und hat nur den Reglerparameter
Schnelle Reaktion auf Änderungen des Sollwerts
Frequenz und Phasengang sind über die Frequenz konstant und damit frequenzunabhängig

zur Videoseite: P Regler

Beliebte Inhalte aus dem Bereich Regelungstechnik

Intro Regelungstechnik I

Regelungstechnik - Grundlagen

Blockschaltbild

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .