Übertragungsfunktion
In diesem Artikel möchten wir dir die Grundlagen zur Übertragungsfunktion näherbringen. Wir zeigen dir ihre Bedeutung, die verschiedenen Darstellungsformen und wie du die Übertragungsfunktion aus einer Differenzialgleichung beziehungsweise aus einer elektrischen Schaltung erstellst.
Wenn du keine Lust hast so viel zu lesen, dann solltest du dir auf jeden Fall unser Video anschauen!
Inhaltsübersicht
Übertragungsfunktion Definition
Die Übertragungsfunktion beschreibt in der Regelungstechnik das Verhältnis vom Ausgangssignal zum Eingangssignal eines dynamischen Systems. Sie wird mit  abgekürzt und im Bildbereich angegeben.
abgekürzt und im Bildbereich angegeben.
Zum Beispiel können alle gängigen Übertragungsglieder aus der Regelungstechnik mit einer Übertragungsfunktion beschrieben werden.
Übertragungsfunktion aus Differenzialgleichung
Eine weitere Methode die Übertragungsfunktion eines Systems zu ermitteln ist, sie aus der Differenzialgleichung des Systems aufzustellen. Dafür wird die Differenzialgleichung aus dem Zeitbereich mittels Laplacetransformation in den Bildbereich transformiert und anschließend das Verhältnis zwischen Ausgangs– und Eingangssignal gebildet. Dies wird weiter unten in diesem Artikel anhand eines Beispiels durchgeführt.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Darstellungsformen der Übertragungsfunktion
Grundsätzlich handelt es sich bei Übertragungsfunktionen in der Regelungstechnik um gebrochen-rationale Funktionen der Form:

Dabei gibt es verschiedene Möglichkeiten der Darstellung.
Pol-Nullstellendarstellung
Für die Pol-Nullstellendarstellung wird das Zähler- und Nennerpolynom linearfaktorzerlegt. Das bedeutet es werden die Nullstellen des jeweiligen Polynoms gefunden und das Polynom auf diese Weise umgeschrieben.

Diese Darstellung kann beispielsweise dafür genutzt werden, um die Reglerparameter eines Reglers so zu bestimmen, dass seine Nullstellen die Polstellen der Regelstrecke aufheben und damit die Gesamtübertragungsfunktion vereinfachen.
Außerdem ist diese Form hilfreich, um den Pol-Nullstellenplan eines Systems aufzustellen und damit Aussagen über ihr Stabilitäts -und Schwingungsverhalten zu treffen.
Zeitkonstantendarstellung
Die Zeitkonstantendarstellung ist eine sehr häufig gewählte Darstellungsform, da die Zeitkonstanten eines Systems messtechnisch, beispielsweise durch die Impuls– oder Sprungantwort, ermittelt werden können.
Die Übertragungsfunktion wird dafür in folgende Form gebracht:

Die Zeitkonstantendarstellung kann beispielsweise zur schnellen Erstellung des Bodediagramms genutzt werden.
Partialbruchdarstellung

Durch Partialbruchzerlegung kann die Übertragungsfunktion in die Partialbruchdarstellung umgewandelt werden. Die Pol-Nullstellendarstellung eignet sich dabei gut als Startpunkt, da hier bereits die Polstellen bestimmt wurden.
Die Partialbruchdarstellung eignet sich besonders gut zur Rücktransformation in den Zeitbereich, da jeder Partialbruch einzeln rücktransformiert und anschließend summiert werden kann. Außerdem lässt sich die Laplacetransformierte eines Partialbruches im Gegensatz zur gesamten Übertragungsfunktion häufig aus einer Korrespondenztabelle für die Laplacetransformation entnehmen.
Aufstellen der Übertragungsfunktion aus einer Differenzialgleichung
Gegeben sei die Differenzialgleichung eines PT1-Systems
mit dem Eingang  und dem Ausgang
und dem Ausgang  :
:

Um daraus die Übertragungsfunktion des Systems zu erhalten wird die Differenzialgleichung zunächst laplacetransformiert.

Nun wird die Gleichung so umgestellt, dass sich auf einer Seite der Gleichung das Verhältnis von Ausgang zu Eingang ergibt. Dazu wird zunächst  ausgeklammert:
ausgeklammert:

Und anschließend das Verhältnis  gebildet:
gebildet:

Die Übertragungsfunktion G(s) eines PT1-Systems lautet also:

Übertragungsfunktion eines Tiefpass-Filters
Gegeben sei ein RC-Tiefpassfilter:
Aus der Abbildung kann entnommen werden, dass es sich bei  um den Eingang und bei
um den Eingang und bei  um den Ausgang handelt. Die Übertragungsfunktion lässt sich für diese Anordnung auf zwei verschiedenen Wegen aufstellen. Zum einen kann man die Differenzialgleichung bestimmen und diese dann in den Bildbereich transformieren. Zum anderen kann mit Hilfe der komplexen Impedanzen der Zusammenhang von
um den Ausgang handelt. Die Übertragungsfunktion lässt sich für diese Anordnung auf zwei verschiedenen Wegen aufstellen. Zum einen kann man die Differenzialgleichung bestimmen und diese dann in den Bildbereich transformieren. Zum anderen kann mit Hilfe der komplexen Impedanzen der Zusammenhang von  und
und  bestimmt werden. Hier wurde der zweite Ansatz gewählt
bestimmt werden. Hier wurde der zweite Ansatz gewählt
Der Zusammenhang von  und
und  ergibt sich über den Spannungsteiler:
ergibt sich über den Spannungsteiler:

Mit 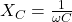 ergibt sich:
ergibt sich:

Nun wird das Verhältnis  gebildet und der Bruch mit
gebildet und der Bruch mit  erweitert:
erweitert:

Die Übertragungsfunktion eines Tiefpasses lautet also:

Beziehungsweise mit 

Der Vergleich zur allgemeinen Übertragungsfunktion eines PT1 Systems zeigt, dass der Proportionalitätsfaktor K des Tiefpasses gleich 1 und seine Zeitkonstante T gleich  ist.
ist.
 und
und 


