PID Regler
Im folgenden Artikel möchten wir dir die Grundlagen des PID-Reglers näherbringen. Dabei gehen wir auf den Aufbau ein und erklären dir außerdem seine Übertragungsfunktion , sowie seine Anwendungen. Schau dir für eine kurze Zusammenfassung am besten unser Video dazu an.
Inhaltsübersicht
Definition des PID-Reglers
 beziehungsweise die Stellgröße
beziehungsweise die Stellgröße  aus Proportional-, Integral- und Differenzial-Anteilen der Regeldifferenz
aus Proportional-, Integral- und Differenzial-Anteilen der Regeldifferenz  gebildet wird.
gebildet wird.Zusätzlich beinhaltet der Regler die Berechnung der Regeldifferenz  aus dem Sollwert und dem Istwert.
aus dem Sollwert und dem Istwert.
P-Anteil
Der P-Anteil der Stellgröße  , wird allein vom aktuellen Wert der Regeldifferenz
, wird allein vom aktuellen Wert der Regeldifferenz  beeinflusst. Dabei ist y(t), wie der Name schon sagt, proportional zum Wert von
beeinflusst. Dabei ist y(t), wie der Name schon sagt, proportional zum Wert von  . Mathematisch lässt sich dieser Zusammenhang folgendermaßen ausdrücken.
. Mathematisch lässt sich dieser Zusammenhang folgendermaßen ausdrücken.

Je größer  ist, desto schneller reagiert der Regler auf Änderungen des Sollwerts.
ist, desto schneller reagiert der Regler auf Änderungen des Sollwerts.
Eine wichtige Unzulänglichkeit eines Reglers, der allein aus einem P-Anteil besteht (P-Regler), ist, dass die Regeldifferenz  nicht zu 0 werden kann und somit Sollwert und Istwert nicht übereinstimmen können. Für die Regeldifferenz im eingeschwungenen Zustand eines geschlossenen Regelkreises mit P-Regler und negativer Rückführung, der mit einem Einheitssprung angeregt wird, gilt:
nicht zu 0 werden kann und somit Sollwert und Istwert nicht übereinstimmen können. Für die Regeldifferenz im eingeschwungenen Zustand eines geschlossenen Regelkreises mit P-Regler und negativer Rückführung, der mit einem Einheitssprung angeregt wird, gilt:

Das bedeutet also, dass zwar durch Erhöhung des Proportionalitätsfaktors  eine beliebig kleine Regeldifferenz erreicht werden kann, gleichzeitig wird aber der Regelkreis für große
eine beliebig kleine Regeldifferenz erreicht werden kann, gleichzeitig wird aber der Regelkreis für große  instabil und neigt zu Schwingungen.
instabil und neigt zu Schwingungen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
I-Anteil
Im Gegensatz zu einem P-Regler, ist die Stellgröße bei einem I-Regler sowohl vom aktuellen Wert der Regeldifferenz als auch von den vergangenen Werten abhängig. Der I-Anteil integriert dabei die Regeldifferenz. Praktisch bedeutet das, dass die vorangegangenen Werte summiert werden. Mathematisch ergibt sich für die Stellgröße  folgende Beziehung:
folgende Beziehung:

Das heißt, dass der Anteil der Stellgröße, für den der I-Regler verantwortlich ist, solange steigt, bis die Regeldifferenz zu Null geworden ist. Solange danach keine Änderungen am Sollwert vorgenommen werden bleibt die Stellgröße konstant. Auf den Faktor  wird weiter unten in unserem Artikel genauer eingegangen.
wird weiter unten in unserem Artikel genauer eingegangen.
Eine wichtige Eigenschaft des I-Reglers ist also, dass die Regeldifferenz zu Null wird und damit der Sollwert und der Istwert des Regelkreises übereinstimmen. Ein Nachteil des I-Reglers ist allerdings, dass er im Allgemeinen nur langsam auf Änderungen des Sollwerts reagiert.
D-Anteil
Der D-Anteil betrachtet nicht die eigentlichen Werte der Regeldifferenz, sondern deren zeitliche Änderung. Dadurch ist es möglich den aktuellen Trend der Regeldifferenz festzustellen und ihren zukünftigen Wert zu schätzen. Entsprechend ist das Ziel eines D-Reglers nicht die Regeldifferenz zu 0 werden zu lassen, sondern, dass keine Änderung der Regeldifferenz mehr auftritt.
Mathematisch ergibt sich die Stellgröße für den D-Anteil zu:

Der Faktor  bestimmt wie viel Einfluss der D-Anteil auf die Stellgröße besitzt, auf ihn wird bei der allgemeinen Gleichung des PID-Reglers genauer eingegangen. Grundsätzlich wird der D-Anteil klein gehalten, da Rauschen auf dem Messsignal für den Istwert unvermeidbar ist und sich damit die Regeldifferenz kontinuierlich ändert.
bestimmt wie viel Einfluss der D-Anteil auf die Stellgröße besitzt, auf ihn wird bei der allgemeinen Gleichung des PID-Reglers genauer eingegangen. Grundsätzlich wird der D-Anteil klein gehalten, da Rauschen auf dem Messsignal für den Istwert unvermeidbar ist und sich damit die Regeldifferenz kontinuierlich ändert.
Der PID-Regler
Werden die drei Anteile nun, wie im Blockschaltbild zu sehen ist, kombiniert, so erhält man einen Regler, der die Eigenschaften der einzelnen Anteile vereint. Dieser wird als PID-Regler bezeichnet. Mathematisch ergibt sich seine Gleichung für die Stellgröße aus der Summe der einzelnen Anteile.

Häufig wird die Reglergleichung auch in folgender Form angegeben:

Dabei wurde  durch
durch  und
und  ersetzt und anschließend
ersetzt und anschließend  ausgeklammert.
ausgeklammert.
Die Nachstellzeit 
 wird als Nachstellzeit des Reglers bezeichnet. Die Nachstellzeit bezeichnet die Zeit, die verstreichen muss, damit der I-Anteil gleich dem P-Anteil ist. Gleichzeitig ist sie ein Maß dafür, wie stark der Einfluss des I-Anteils ist. Je größer die Nachstellzeit ist, desto geringer ist der Einfluss des I-Anteils und umgekehrt.
wird als Nachstellzeit des Reglers bezeichnet. Die Nachstellzeit bezeichnet die Zeit, die verstreichen muss, damit der I-Anteil gleich dem P-Anteil ist. Gleichzeitig ist sie ein Maß dafür, wie stark der Einfluss des I-Anteils ist. Je größer die Nachstellzeit ist, desto geringer ist der Einfluss des I-Anteils und umgekehrt.
Übertragungsfunktion des PID-Reglers
Durch Laplacetransformation der Reglergleichung lässt sich die Übertragungsfunktion des PID-Reglers im Bildbereich aufstellen.

Das Vorgehen ist dabei wie folgt. Zuerst werden die einzelnen Bestandteile der Gleichung in den Bildbereich überführt.
Aus:

Wird:

Da die Übertragungsfunktion das Verhältnis von Ausgansgröße zur Eingangsgröße darstellt, muss die Gleichung nun noch in die Form  gebracht werden.
gebracht werden.
Dafür wird zunächst  ausgeklammert:
ausgeklammert:

und anschließend auf die andere Seite der Gleichung gebracht:

Für eine anschaulichere Darstellung der Gleichung werden die Terme innerhalb der Klammer noch auf den gleichen Nenner gebracht:

Polstellen-Kompensation
Eine wichtige Eigenschaft des PID-Reglers ist die Möglichkeit, die Polstellen einer Regelstrecke durch eigene Nullstellen zu kompensieren. Dafür wird das Zählerpolynom der Übertragungsfunktion faktorisiert, indem dessen Nullstellen gefunden werden:

Die Nullstellen des Zählerpolynoms ergeben sich zu:

Damit lässt sich die Übertragungsfunktion des PID-Reglers in folgender Form darstellen:

mit 
Die sich so im Nenner ergebenden Nullstellen können genutzt werden, um Pole der Regelstrecke zu kompensieren und damit den Regelkreis zu vereinfachen. Dafür müssen die Zeitkonstanten T1 bzw. T2 den Zeitkonstanten der Pole der Regelstrecke entsprechen. Es bietet sich an vor allem instabile Pole oder langsame Zeitkonstanten zu kompensieren, um die Übertragungsfunktion des Systems zu vereinfachen.


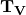
 ist ein Maß für den Einfluss des D-Anteils. Sie gibt an wie weit in die Zukunft der der aktuelle Trend (Steigung) der Regelgröße angenommen werden soll.
ist ein Maß für den Einfluss des D-Anteils. Sie gibt an wie weit in die Zukunft der der aktuelle Trend (Steigung) der Regelgröße angenommen werden soll.