Dieser Artikel behandelt das Blockschaltbild. Dabei wird erläutert, wo Blockschaltbilder Anwendung finden, wie Sie aufgebaut sind, was eine Übertragungsfunktion ist und wie Blockschaltbilder vereinfacht werden können.
Wenn du alle Informationen einfach und schnell zusammengefasst haben möchtest, kannst du dir auch unser Video zum Thema Blockschaltbild ansehen. Damit verstehst du alles rund ums Thema in kürzester Zeit.
Blockschaltbild Definition
Das wohl bekannteste Beispiel eines Blockschaltbildes in der Regelungstechnik ist das des geschlossenen Regelkreises.
Blockschaltbild Übertragungsfunktion
Allgemein ist das Ziel der Regelungstechnik den Zusammenhang zwischen Ein- und Ausgangsgrößen eines Systems zu beschreiben. Die Funktion eines Systems, die genau das macht, wird Übertragungsfunktion genannt. Sie wird mit G bezeichnet und ist in der Regel direkt im Bildbereich angegeben. Wenn du zur Übertragungsfunktion mehr wissen möchtest, schau dir unbedingt unser Video dazu an. Hier wird dir die Bedeutung der Übertragungsfunktion sowie die verschiedenen Darstellungsformen erläutert und wie die Übertragungsfunktion aus einer Differenzialgleichung beziehungsweise aus einer elektrischen Schaltung abgeleitet werden kann.
Blöcke
Die wichtigsten Bestandteile des Blockschaltbilds sind die Blöcke. Wir konzentrieren uns hier auf Blöcke mit nur einem Ein- und Ausgang. Das Signal, dessen Pfeil in Richtung des Blockes deutet, entspricht dem Eingang 
und das Signal, das aus ihm herauskommt, dem Ausgang 
. Jeder Block kann durch eine Übertragungsfunktion G beschrieben werden. Typische Blöcke sind zum Beispiel das P, I und D-Glied.
Summierstelle
Neben den eigentlichen Blöcken ist ein elementarer Bestandteil eines Blockschaltbilds die Summierstelle. Sie wird genutzt, um Signale miteinander zu addieren beziehungsweise zu subtrahieren. Die Summierstelle wird durch einen Kreis symbolisiert. Dabei sind Signale, deren Pfeile in Richtung des Kreises deuten, die Eingänge. Das Signal, das aus dem Kreis herauskommt, ist der Ausgang. Soll an der Summierstelle eine Subtraktion vorgenommen werden, dann ist ein Minuszeichen an den Pfeil des entsprechenden Eingangssignals angefügt. Steht kein Symbol, oder ein Plus am Pfeil, erfolgt eine Addition.
Verzweigung
Ein weiterer wesentlicher Bestandteil eines Blockschaltbilds sind die Verzweigungen. Sie werden genutzt, um ein Signal aufzuteilen und auf mehrere Blöcke zu führen.
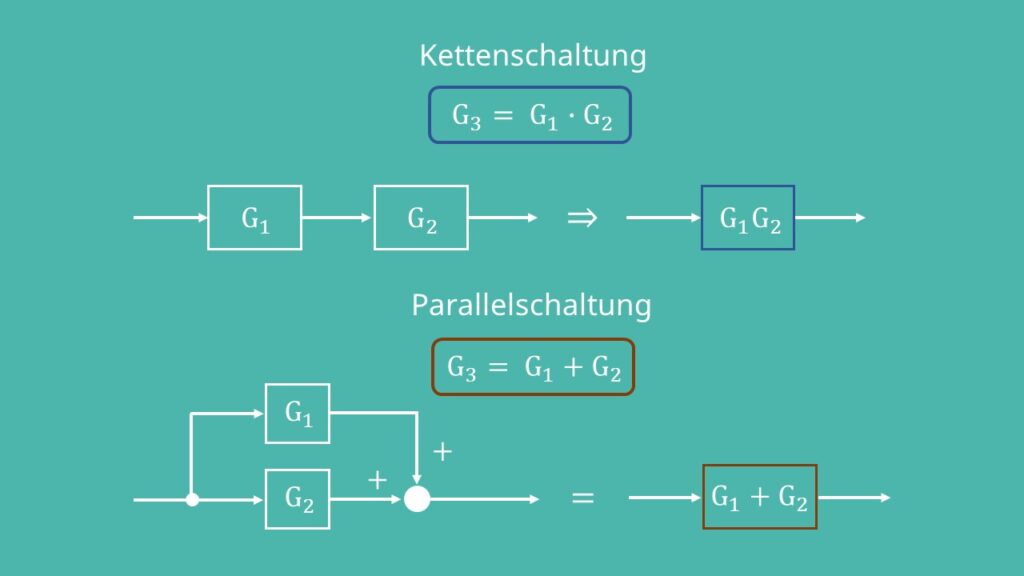
zusammenfassen.Parallelschaltung
Eine weitere geläufige Anordnung ist die Parallelschaltung. Dabei haben die beiden Blöcke dasselbe Eingangssignal. Ihre Ausgänge werden summiert. Sind die Blöcke mit den Übertragungsfunktionen 
und 
in einer Parallelschaltung angeordnet, so kannst du sie zu einem Block mit der Übertragungsfunktion 
zusammenfassen.
Rückkopplung
Etwas komplizierter ist die Rückkopplungsschleife. Sie besteht aus einen Vorwärtszweig mit der Übertragungsfunktion 
und einem Rückwärtszweig mit der Übertragungsfunktion 
. Eine Rückkopplungsschleife lässt sich mit der Formel
zusammenfassen. Dabei solltest du unbedingt auf den Nenner achten. Wird das Ausgangssignal vom Eingang abgezogen, so ist die verwendete Rechenoperation im Nenner eine Addition. Das bedeutet, es steht ein Minus am Pfeil an der Summierstelle. Wird hingegen der Ausgang zum Eingang hinzugerechnet, dann erfolgt im Nenner eine Subtraktion. In diesen Fall steht ein Plus an der Summierstelle.
Führungsübertragungsfunktion
Mit den Komponenten eines Blockschaltbildes und der Blockschaltbild-Algebra kann die Gesamtübertragungsfunktion eines Blockschaltbildes bestimmt werden. Hierfür werden solange Blöcke subsummiert, bis zwischen Ein- und Ausgang nur noch ein Block übrigbleibt. Die Übertragungsfunktion dieses Blockes ist die Gesamtübertragungsfunktion oder auch Führungsübertragungsfunktion. Die Führungsübertragungsfunktion 
ist damit als das Verhältnis von Ausgang zu Eingang definiert.
Für das Beispiel ergibt sich für die Führungsübertragungsfunktion unter Berücksichtigung der Kettenschaltung und Rückkopplung:
Mit 
und 
ergibt sich schließlich:
