Stehende Welle
Kannst du erraten, was Musikinstrumente, Mikrowellen und Laser gemeinsam haben? Das sollte für dich kein Problem sein, denn du hast bestimmt danach gesucht: stehende Wellen. In diesem Beitrag lernst du was eine stehende Welle ist und wie eine stehende Welle entstehen kann.
Bevor wir loslegen, möchten wir dich auf unser Video zum Thema stehende Welle aufmerksam machen. Durch das Verbinden des Lesens mit einer audiovisuellen Unterstützung, fällt es dir leichter das Gelernte im Gedächtnis zu behalten.
Inhaltsübersicht
Stehende Welle einfach erklärt
Bei der stehenden Welle handelt es sich um ein festes Muster aus Schwingungsknoten (manchmal auch Wellenknoten) und Schwingungsbäuche (oder Wellenbäuche), das mit bestimmen Frequenzen, den Resonanz- oder Eigenfrequenzen , auf und ab schwingt. Eine stehende Welle kannst du bspw. durch das Einspannen eines Seils realisieren.
Eine stehende Welle (seltener auch Stehwelle) entsteht bei der Interferenz zweier Wellen mit gleicher Amplitude und Frequenz , die sich in entgegengesetzter Richtung bewegen.
Stehende Welle Formel
Für den weiteren Verlauf des Beitrags beschäftigen wir uns mit einem Seil, bei dem sich beide Seilenden nicht bewegen dürfen. Du kannst dir hierfür eine Gitarrensaite vorstellen. Wir hatten im vorherigen Absatz erwähnt, dass nur für bestimmte Frequenzen stehende Wellen entstehen. Diese Frequenzen nennt man Resonanz- oder Eigenfrequenzen des Seils. Du kannst sie mit folgender Formel berechnen
 .
.
Unter  ist diejenige Frequenz zu verstehen, mit denen die Bäuche des
ist diejenige Frequenz zu verstehen, mit denen die Bäuche des  -ten Musters auf und ab schwingen. Hier ist
-ten Musters auf und ab schwingen. Hier ist  die Ausbreitungsgeschwindigkeit der Welle in
die Ausbreitungsgeschwindigkeit der Welle in  und
und  die Länge des Seils in
die Länge des Seils in  . Der Buchstabe
. Der Buchstabe  soll Auskunft darüber geben, um welches Muster es sich handelt (mehr Details weiter unten) und besitzt keine Einheit. Aus dem Zusammenhang
soll Auskunft darüber geben, um welches Muster es sich handelt (mehr Details weiter unten) und besitzt keine Einheit. Aus dem Zusammenhang

kannst du für jede Resonanzfrequenz die dazugehörige Wellenlänge der stehende Welle berechnen
 .
.
An dieser Stelle weißt du bereits, dass eine stehende Welle ein festes Muster aus Knoten und Bäuchen ist. Dieses Muster wollen wir genauer charakterisieren. Beginnen wir erstmal mit ein paar weiteren wichtigen Bezeichnungen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Grundschwingung und weitere Harmonische
Für  erhalten wir ein Muster, das Grundschwingung oder erste Harmonische genannt wird. Die dazugehörige Frequenz heißt Grundfrequenz des Seils. Verdoppeln bzw. verdreifachen wir die Grundfrequenz, erhalten wir die zweite bzw. dritte Harmonische (auch 1. Oberschwingung bzw. 2. Oberschwingung genannt). Natürlich kannst du die Grundfrequenz auch vervierfachen und würdest die vierte Harmonische (oder 3. Oberschwingung) erhalten, usw.
erhalten wir ein Muster, das Grundschwingung oder erste Harmonische genannt wird. Die dazugehörige Frequenz heißt Grundfrequenz des Seils. Verdoppeln bzw. verdreifachen wir die Grundfrequenz, erhalten wir die zweite bzw. dritte Harmonische (auch 1. Oberschwingung bzw. 2. Oberschwingung genannt). Natürlich kannst du die Grundfrequenz auch vervierfachen und würdest die vierte Harmonische (oder 3. Oberschwingung) erhalten, usw.
Jedes dieser Muster besitze eine feste Anzahl an Schwingungsknoten und Schwingungsbäuchen. Diese Anzahl kannst du folgendermaßen leicht ausrechnen.
Schwingungsknoten
Schwingungsknoten sind Orte, an denen das Seil keine Auslenkung erfährt. Es gibt hierzu zwei wichtige Formeln

und
 .
.
Schwingungsbäuche
Schwingungsbäuche sind Orte, an denen das Seil maximale Auslenkung erfährt. Es gibt hierzu zwei wichtige Formeln

und
 .
.
Charakterisierung des Wellenmusters Beispiel
Die obigen Formeln bedeutet also, dass bspw. die Fundamentale keine Knoten und einen Bauch, oder die dritte Harmonische zwei Knoten und drei Bäuche besitzt. Der erste Schwingungsbauch tritt immer im Abstand von 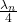 , der erste Schwingungsknoten im Abstand von
, der erste Schwingungsknoten im Abstand von  zum linken Seilende auf. Alle anderen Positionen erhälst du durch Addition von
zum linken Seilende auf. Alle anderen Positionen erhälst du durch Addition von  . Zum Beispiel befinden sich die Bäuche bei der dritten Harmonische an den Stellen
. Zum Beispiel befinden sich die Bäuche bei der dritten Harmonische an den Stellen 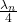 ,
,  und
und  .
.
Stehende Welle Entstehung
Nun kannst du Dir eine stehende Welle vorstellen und die ein oder andere Kenngröße ausrechnen. In diesem Absatz wollen wir uns der Frage widmen, wie eine stehende Welle entstehen kann.
Für die Entstehung einer stehenden Welle benötigen wir zwei Komponenten: Reflexion und Interferenz . Lenkst du das eingespannte Seil mit einer harmonischen Bewegung aus, dann werden an beiden Seilenden die Wellen reflektiert. Diese bewegen sich dann in die andere Richtung. Wählst du die Schwingfrequenz zufällig aus, dann interferieren die reflektierten Wellen nach einem willkürlichen Muster miteinander. Du würdest hier keine besonderen Beobachtungen machen können.
Schwingst du aber das Seil mit einer seiner Resonanzfrequenzen aus, dann interferieren die Wellen gerade so, dass sie ein stationäres Muster bilden. Die Knoten entsprechen dann Orte der destruktiven, die Bäuche Orte der konstruktiven Interferenz. Du kannst weitere Details hierzu in unserem Beitrag zur Bragg-Gleichung finden.
Sollte dich der Lehrer oder Professor nach der Entstehung von stehenden Wellen fragen, dann kannst du nun mit Zuversicht sagen: Eine stehende Welle entsteht durch die Interferenz zweier Wellen mit gleicher Amplitude und Frequenz, die sich in entgegengesetzter Richtung bewegen.
