Video

Quiz

Hier geht's zum Video „Vektorrechnung“

Vektoren addieren und subtrahieren

Wichtige Inhalte in diesem Video

Vektoren addieren und subtrahieren einfach erklärt

Vektoren addieren

Vektoren subtrahieren

Du sollst zwei Vektoren addieren oder subtrahieren? Hier und im Video erfährst du alles, was du dazu wissen musst.

Inhaltsübersicht

Vektoren addieren und subtrahieren einfach erklärt

im Videozur Stelle im Video springen

Du addierst oder subtrahierst zwei Vektoren, indem du Zeile für Zeile der beiden Vektoren verrechnest. Das Ergebnis jeder Zeile stellst du in einem neuen Vektor, dem Ergebnisvektor, dar. Dabei ist es egal, ob die Vektoren mit einem Plus oder einem Minus verbunden sind.

$\left( \begin{array}{c} \textcolor{orange}{1} \\ \textcolor{blue}{2} \\ \textcolor{olive}{3} \end {array} \right) + \left( \begin{array}{c} \textcolor{orange}{7} \\ \textcolor{blue}{8} \\ \textcolor{olive}{9} \end {array} \right) = \left( \begin{array}{c} \textcolor{orange}{1 + 7} \\ \textcolor{blue}{2 + 8} \\ \textcolor{olive}{3 + 9} \end {array} \right) = \left( \begin{array}{c} \textcolor{orange}{8} \\ \textcolor{blue}{10} \\ \textcolor{olive}{12} \end {array} \right)$

$\left( \begin{array}{c} \textcolor{orange}{8} \\ \textcolor{olive}{5} \end {array} \right) - \left( \begin{array}{c} \textcolor{orange}{3} \\ \textcolor{olive}{4} \end {array} \right) = \left( \begin{array}{c} \textcolor{orange}{8 - 3} \\ \textcolor{olive}{5 - 4} \end {array} \right) = \left( \begin{array}{c} \textcolor{orange}{5} \\ \textcolor{olive}{1} \end {array} \right)$

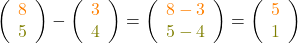
Wichtig dabei ist, dass du nur Vektoren mit der gleichen Anzahl von Zeilen verrechnest. Einen zweizeiligen kannst du nicht mit einem dreizeiligen Vektor addieren oder subtrahieren.

Vektoren addieren

im Videozur Stelle im Video springen

Auf die Lösung einer Vektoraddition kommst du sowohl durchs Rechnen als auch durchs Zeichnen. In den folgenden Absätzen erfährst du mehr darüber, wie du den Ergebnisvektor zeichnen kannst und nach welchen Schritten du dabei vorgehst.

Graphische Darstellung

Um die Addition von zwei Vektoren zu verstehen, kannst du sie dir wie eine Wegbeschreibung vorstellen. Du hast zum Beispiel diese beiden Vektoren gegeben:

$\vec{\textcolor{blue}{a}} = \left( \begin{array}{c} 5 \\ 1 \end {array} \right)$

$\vec{\textcolor{cyan}{b}} = \left( \begin{array}{c} 2 \\ 3 \end {array} \right)$

Dann sagt dir der Vektor $\vec{\textcolor{blue}{a}}$ , dass du 5 nach rechts und 1 nach oben gehen musst. Für Vektor $\vec{\textcolor{cyan}{b}}$ gehst du 2 nach rechts und 3 nach oben.

Wenn du jetzt den Vektor $\vec{\textcolor{cyan}{b}}$ zum Vektor $\vec{\textcolor{blue}{a}}$ hinzuaddierst, dann ist das eine Aneinanderreihung von den zwei Wegbeschreibungen. Du gehst also erst 5 nach rechts und 1 nach oben und dann nochmal 2 nach rechts und 3 nach oben.

Um nun aber keinen Umweg zu machen, kannst du auch direkt 7 nach rechts und 4 nach oben gehen, anstatt beide Wege nacheinander zu gehen. Das ist dann die Summe der beiden Vektoren und dein Ergebnisvektor $\vec{\textcolor{green}{c}}$ .

$\vec{\textcolor{green}{c}} = \vec{\textcolor{blue}{a}} + \vec{\textcolor{cyan}{b}} = \left( \begin{array}{c} 7 \\ 4 \end {array} \right)$

Vektoren, Vektoren addieren, Vektoraddition, zwei Vektoren addieren, Vektoren graphisch addieren, zwei Vektoren graphisch addieren, zwei Vektoren zusammenrechnen, Ergebnisvektor, Ergebnisvektor nach Addition — Vektoren graphisch addieren

Anleitung — Vektoraddition

Beliebigen Startpunkt suchen
Vektor $\vec{a}$ einzeichnen
Vektor $\vec{b}$ an Vektor $\vec{a}$ anhängen
Anfangs- und Endpunkt verbinden
Ergebnisvektor $\vec{c}$ ablesen

Berechnung

Genauso kannst du den Vektor $\vec{\textcolor{green}{c}}$ aber auch berechnen.

$\vec{\textcolor{green}{c}} = \vec{\textcolor{blue}{a}} + \vec{\textcolor{cyan}{b}} = \left( \begin{array}{c} 5 \\ 1 \end {array} \right) + \left( \begin{array}{c} 2 \\ 3 \end {array} \right) = \left( \begin{array}{c} 7 \\ 4 \end {array} \right)$

Allgemeine Formel

Allgemein kannst du dir folgende Formeln merken, wenn du zwei Vektoren addieren willst:

$\left( \begin{array}{c} x_1 \\ y_1 \\ z_1 \end{array} \right) + \left( \begin{array}{c} x_2 \\ y_2 \\ z_2 \end{array} \right) = \left( \begin{array}{c} x_1 + x_2 \\ y_1 + y_2 \\ z_1 + z_2 \end{array} \right) = \left( \begin{array}{c} x \\ y \\ z \end{array} \right)$

Vektoren subtrahieren

im Videozur Stelle im Video springen

Willst du zwei Vektoren subtrahieren, dann gibt es auch hier zwei Möglichkeiten, wie du den Ergebnisvektor bestimmen kannst. Entweder zeichnest du die Vektoren und bestimmst so den Ergebnisvektor oder du ziehst die Vektoren voneinander ab und berechnest so das Ergebnis.

Graphische Darstellung

Den Ergebnisvektor einer Subtraktion kannst du auch graphisch als bestimmen.

$\vec{\textcolor{blue}{d}} = \left( \begin{array}{c} 4 \\ 4 \end {array} \right)$

$\vec{\textcolor{cyan}{e}} = \left( \begin{array}{c} -4 \\ 2 \end {array} \right)$

Zeichne dafür den ersten Vektor $\vec{\textcolor{blue}{d}}$ auf deinem Papier auf. Stellst du ihn dir wieder als Wegbeschreibung vor, musst du 4 nach rechts und 4 nach oben gehen.

Willst du nun den Vektor $\vec{\textcolor{cyan}{e}}$ davon abziehen, gehst du den Weg, den er dir beschriebt, rückwärts. Du gehst also 4 nach rechts und 2 nach unten, anstatt 4 nach links und 2 nach oben.

Um jetzt die Differenz der Vektoren, also den Ergebnisvektor $\vec{\textcolor{green}{f}}$ , zu erhalten, gehst du wieder den direkten Weg. Du gehst also 8 nach rechts und 2 nach oben, anstatt beide Weg hintereinander zu gehen.

$\vec{\textcolor{green}{f}} = \vec{\textcolor{blue}{d}} - \vec{\textcolor{cyan}{e}} = \left( \begin{array}{c} 8 \\ 2 \end {array} \right)$

Vektoren, Vektoren subtrahieren, Vektoren graphisch subtrahieren, Vektoren zeichnen, Vektoren voneinander abziehen — Vektoren graphisch subtrahieren

Darstellung mit dem Gegenvektor

Um die Differenz der Vektoren zu erhalten, kannst du alternativ auch wie bei der Addition vorgehen und mit dem Gegenvektor – $\textcolor{cyan}{\vec{e}}$ arbeiten. Um den Gegenvektor zu bekommen, drehst du die Vorzeichen von $\textcolor{cyan}{\vec{e}}$ um.

$\textcolor{cyan}{-}\vec{\textcolor{cyan}{e}} = -\left( \begin{array}{c} -4 \\ 2 \end {array} \right) = \left( \begin{array}{c} 4 \\ -2 \end {array} \right)$

Vektoren subtrahieren, Vektoren graphisch subtrahieren, Gegenvektor, Vektoren, Vektor, Ergebnisvektor, Ergebnisvektor einer Subtraktion, Vektorsubtraktion, Vektoraddition, Vektoren addieren — Vektor graphisch subtrahieren mit Gegenvektor

Du zeichnest also den Vektor $\vec{\textcolor{blue}{d}}$ und den Gegenvektor $-\vec{\textcolor{cyan}{e}}$ aneinander und liest den Ergebnisvektor $\vec{\textcolor{green}{f}}$ aus deiner Zeichnung ab.

$\vec{\textcolor{green}{f}} = \vec{\textcolor{blue}{d}} + (-\vec{\textcolor{cyan}{e}}) = \left( \begin{array}{c} 8 \\ 2 \end {array} \right)$

Du erkennst, dass das Ergebnis bei beiden Methoden das gleiche ist.

Anleitung — Vektorsubtraktion

Beliebigen Startpunkt suchen
Vektor $\vec{d}$ einzeichnen
Vektor $\vec{e}$ umgekehrt einzeichnen oder Gegenvektor – $\vec{e}$ anhängen
Anfangs- und Endpunkt der Vektorkette verbinden
$\vec{f}$ ablesen

Berechnung

Den Ergebnisvektor $\vec{\textcolor{green}{f}}$ kannst du genauso, wie bei der Addition auch, berechnen.

$\vec{\textcolor{green}{f}} = \vec{\textcolor{blue}{d}} - \vec{\textcolor{cyan}{e}} = \left( \begin{array}{c} 4 \\ 4 \end {array} \right) - \left( \begin{array}{c} -4 \\ 2 \end {array} \right) = \left( \begin{array}{c} 4 - (-4) \\ 4 - 2 \end {array} \right) = \left( \begin{array}{c} 8 \\ 2 \end {array} \right)$

Allgemeine Formel

Allgemein kannst du dir folgende Formeln merken, wenn du zwei Vektoren subtrahieren willst:

$\left( \begin{array}{c} x_1 \\ y_1 \\ z_1 \end{array} \right) - \left( \begin{array}{c} x_2 \\ y_2 \\ z_2 \end{array} \right) = \left( \begin{array}{c} x_1 - x_2 \\ y_1 - y_2 \\ z_1 - z_2 \end{array} \right) = \left( \begin{array}{c} x \\ y \\ z \end{array} \right)$

Vektoren addieren und subtrahieren — häufigste Fragen

Wie kann man Vektoren addieren?
Zwei Vektoren addierst oder subtrahierst du, indem du die Vektoren komponentenweise verrechnest und das Ergebnis im Ergebnisvektor darstellst. Dabei ist es egal, ob die Vektoren mit einem Plus oder einem Minus verbunden sind.
Wann kann man Vektoren addieren?
Vektoren kannst du addieren und subtrahieren, wenn sie die gleiche Anzahl von Zeilen haben. Sonst ist eine Berechnung nicht möglich.
Wie funktioniert eine Vektoraddition?
Um zwei Vektoren graphisch zu addieren, setzt du den Anfangspunkt des zweiten Vektors an den Endpunkt des ersten Vektors. Den resultierenden Vektor bildest du, indem du den Startpunkt des ersten Vektors und den Endpunkt des zweiten Vektors mit einem Pfeil verbindest.

Vektorrechnung

Prima! Jetzt weißt du, wie man Vektoren sowohl graphisch als auch rechnerisch addiert und subtrahiert. Willst du mehr über das Thema Vektorrechnung erfahren? Dann schau unbedingt hier im Video dazu vorbei.

Zum Video: Vektorrechnung

zur Videoseite: Vektoren addieren und subtrahieren

Beliebte Inhalte aus dem Bereich Lineare Algebra

Vektor berechnen

Vektoren addieren und subtrahieren

Lineare Unabhängigkeit und lineare Abhängigkeit von Vektoren

Linearkombination

Mittelpunkt einer Strecke berechnen

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .