Inverse 2×2
Hier lernst du, wie du ganz schnell und einfach eine inverse 2×2 Matrix berechnen kannst. Du möchtest das Thema lieber visuell erklärt bekommen? Dann schau dir unser Video an!
Inhaltsübersicht
Inverse 2×2 einfach erklärt
Die Inverse einer 2×2 Matrix kannst du wirklich schnell mit einer Formel bestimmen.

Damit kannst du jede inverse Matrix 2×2 berechnen.
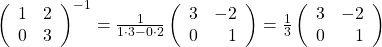
Dabei berechnest du zuerst  , also Hauptdiagonale minus Nebendiagonale, und ziehst das Ergebnis in den Nenner des Bruchs. Anschließend musst du nur noch die Zahlen oben links und unten rechts vertauschen und das Vorzeichen unten links und oben rechts einmal ändern.
, also Hauptdiagonale minus Nebendiagonale, und ziehst das Ergebnis in den Nenner des Bruchs. Anschließend musst du nur noch die Zahlen oben links und unten rechts vertauschen und das Vorzeichen unten links und oben rechts einmal ändern.
Hinweis: Es gibt auch eine andere Möglichkeit, wie du eine 2×2 Matrix invertieren kannst.
Inverse 2×2 Matrix – Beispiel
Schau dir diese 2×2 Matrix einmal an.

Diese Matrix ist quadratisch und hat eine Determinante  . Deshalb existiert eine inverse Matrix
. Deshalb existiert eine inverse Matrix
 . Um diese zu berechnen, gehst du die Formel Schritt für Schritt durch.
. Um diese zu berechnen, gehst du die Formel Schritt für Schritt durch.
Zuerst berechnest du die Determinante, also  . In diesem Beispiel rechnest du also
. In diesem Beispiel rechnest du also  , weil
, weil  ,
,  ,
,  und
und  ist. Dann musst du nur noch die Zahlen in der Hauptdiagonale, also 1 und 3, vertauschen und vor die beiden Zweien ein Minus setzen. Weil der Bruch vor der Matrix in diesem Fall
ist. Dann musst du nur noch die Zahlen in der Hauptdiagonale, also 1 und 3, vertauschen und vor die beiden Zweien ein Minus setzen. Weil der Bruch vor der Matrix in diesem Fall  ergibt, tauschen sich nochmal alle Vorzeichen in der Matrix, wenn du das Ergebnis zusammenfasst.
ergibt, tauschen sich nochmal alle Vorzeichen in der Matrix, wenn du das Ergebnis zusammenfasst.


In diesem Beispiel ist zufällig  . Häufig ergeben sich an dieser Stelle jedoch Brüche, wenn die Determinante größer als 1 oder kleiner als -1 ist. Diese Brüche kannst du gerne vor die inverse Matrix ziehen.
. Häufig ergeben sich an dieser Stelle jedoch Brüche, wenn die Determinante größer als 1 oder kleiner als -1 ist. Diese Brüche kannst du gerne vor die inverse Matrix ziehen.
Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Inverse Matrix 2×2
Vielleicht hast du schon bemerkt, dass in der Formel die Determinante der 2×2 Matrix vorkommt.

Das ergibt natürlich nur Sinn, wenn  . Das ist allerdings immer der Fall, wenn du diese Formel anwendest. Denn Matrizen mit Determinante gleich 0 sind gar nicht invertierbar.
. Das ist allerdings immer der Fall, wenn du diese Formel anwendest. Denn Matrizen mit Determinante gleich 0 sind gar nicht invertierbar.
Außerdem kannst du schnell erkennen, dass die Formel für die inverse 2×2 Matrix stimmt. Lass uns das einmal gemeinsam verifizieren.
Allgemein gilt immer
 .
.
Für die Inverse 2×2 gilt

 .
.
Die Formel ergibt also wirklich die inverse 2×2 Matrix.