Orthogonale Projektion Klausuraufgabe
Nachfolgend findest du eine Aufgabe, mit der du dich auf deine Klausur vorbereiten kannst:
In der Aufgabenstellung ist die Matrix A

und die Definition des Skalarprodukts  gegeben:
gegeben:

für alle 
Außerdem seien die Vektoren  ,
,  und
und  folgendermaßen angeben:
folgendermaßen angeben:
 ,
,  und
und 
Bestimme nun bezüglich des gegebenen Skalarprodukts 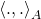 die orthogonale Projektion von
die orthogonale Projektion von  auf den von
auf den von  und
und  aufgespannten Untervektorraum
aufgespannten Untervektorraum  .
.
Du musst bei dieser Aufgabe vor allem darauf achten nicht das Standardskalarprodukt zu wählen, sondern mit dem hier vorgegebenen Skalarprodukt zu arbeiten.
Die Lösung zu dieser Aufgabe mit einem verständlichen Rechenweg findest du in unserem Klausurvideo .