Laplacescher Entwicklungssatz
Der Laplacesche Entwicklungssatz hilft dir, Determinanten zu berechnen. Du möchtest schnell verstehen, wie das funktioniert? Dann schau dir unser Video dazu an!
Inhaltsübersicht
Laplacescher Entwicklungssatz einfach erklärt
Der Laplacesche Entwicklungssatz (auch Laplace Entwicklung, Laplacesche Entwicklung) ist ein Verfahren mit dem du die Determinante einer nxn Matrix berechnen kannst. Die Idee dabei ist, dass du die Determinante einer Matrix auf eine kleinere Determinante bringst. Damit kannst du zum Beispiel eine 4×4 Matrix zunächst auf eine 3×3 Matrix umformen und dann auf eine 2×2 Matrix. Anschließend kannst du dann von dieser Matrix einfach die Determinante berechnen.
 , wenn du nach der i-ten Zeile entwickelst oder
, wenn du nach der i-ten Zeile entwickelst oder
 , wenn du nach der j-ten Spalte entwickelst.
, wenn du nach der j-ten Spalte entwickelst.
Dabei ist  der Wert der i-ten Zeile und j-ten Spalte und
der Wert der i-ten Zeile und j-ten Spalte und  die Matrix, die durch das Streichen der i-ten Zeile und j-ten Spalte der Matrix A entsteht.
die Matrix, die durch das Streichen der i-ten Zeile und j-ten Spalte der Matrix A entsteht.
Tipp: Wähle für den Laplace Entwicklungssatz am besten eine Zeile oder eine Spalte, in der sich möglichst viele Nullen befinden, sodass die entsprechenden Summanden automatisch wegfallen.
Laplacescher Entwicklungssatz Beispiel
In diesem Abschnitt zeigen wir dir an einem konkreten Beispiel, wie du den Laplaceschen Entwicklungssatz anwendest.
Betrachte dafür die 3×3 Matrix  . Dabei spielt es keine Rolle nach welcher Zeile oder Spalte du die Determinante entwickelst. In diesem Beispiel wählen wir die erste Zeile
. Dabei spielt es keine Rolle nach welcher Zeile oder Spalte du die Determinante entwickelst. In diesem Beispiel wählen wir die erste Zeile  . Die Determinante von A lautet also
. Die Determinante von A lautet also


Das bedeutet, dass du nun Spalte für Spalte die einzelnen Summanden der Formel bestimmst.
Spalte 1: Fange mit der ersten Spalte an. Dafür benötigst du die Untermatrix  , die du bekommst, indem du die erste Zeile und die erste Spalte von A streichst
, die du bekommst, indem du die erste Zeile und die erste Spalte von A streichst
Die Matrix  lautet also
lautet also
 .
.
Als nächstes benötigst du die Determinante der 2×2 Matrix
 . Du berechnest die Determinante, indem du vom Produkt
. Du berechnest die Determinante, indem du vom Produkt  das Produkt
das Produkt  abziehst
abziehst
 .
.
Außerdem kannst du aus der Matrix A ablesen, dass  ist. Damit erhältst du für den ersten Summanden
ist. Damit erhältst du für den ersten Summanden

Spalte 2: Gehe nun über zur zweiten Spalte. Um die Untermatrix  zu bekommen streichst du die erste Zeile und die zweite Spalte von A
zu bekommen streichst du die erste Zeile und die zweite Spalte von A
Du erhältst damit
 .
.
Berechne nun die Determinante der Matrix
 .
.
Der zweite Summand lautet mit 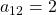 also
also
 .
.
Spalte 3: Wiederhole das Ganze noch für die dritte Spalte. Du erhältst die Untermatrix 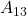 durch das Streichen der ersten Zeile und der dritten Spalte.
durch das Streichen der ersten Zeile und der dritten Spalte.
Sie lautet somit
 .
.
Berechne nun wieder die Determinante der Matrix 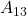
 .
.
Damit hast du nun den dritten Summanden der Formel des Laplaceschen Entwicklungssatzes bestimmt
 .
.
Insgesamt lautet die Determinante der Matrix A also


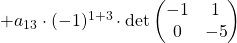

 .
.
Bemerkung: Um das Vorzeichen  einfacher zu bestimmen, kannst du dir auch einfach merken, dass bei jedem Wechsel einer Zeile oder Spalte, sich auch das Vorzeichen ändert.
einfacher zu bestimmen, kannst du dir auch einfach merken, dass bei jedem Wechsel einer Zeile oder Spalte, sich auch das Vorzeichen ändert.

Studyflix vernetzt: Hier ein Video aus einem anderen Bereich
Matrix nach einer Spalte entwickeln
Schau dir als nächstes Beispiel die Matrix  an. Diesmal entwickeln wir die Determinante nach der zweiten Spalte, womit die Determinante von A wie folgt lautet:
an. Diesmal entwickeln wir die Determinante nach der zweiten Spalte, womit die Determinante von A wie folgt lautet:

Du bestimmst also als erstes die Untermatrizen  ,
,  und
und  , indem du die zweite Spalte und die entsprechende Zeile streichst. Die Untermatrizen sehen somit wie folgt aus
, indem du die zweite Spalte und die entsprechende Zeile streichst. Die Untermatrizen sehen somit wie folgt aus
 .
.
Als nächstes benötigst du die Determinante der Untermatrizen



Somit kannst du nun die Determinante der Matrix A berechnen


Laplacescher Entwicklungssatz 4×4 Matrix
Bisher hast du den Laplace Entwicklungssatz nur auf 3×3 Matrizen angewendet. Du kannst die Laplace Entwicklung allerdings auch auf größere Matrizen anwenden, wie etwa 4×4 Matrizen.
Betrachte zum Beispiel die Matrix  , deren Determinante wir nach der vierten Spalte entwickeln.
, deren Determinante wir nach der vierten Spalte entwickeln.
Zunächst benötigst du die Untermatrizen  ,
,  ,
,  und
und 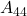 , für die du die vierte Spalte und die entsprechende Zeile der Matrix A streichst. Die Untermatrizen lauten somit
, für die du die vierte Spalte und die entsprechende Zeile der Matrix A streichst. Die Untermatrizen lauten somit
 ,
,  ,
,  ,
, 
Um die Determinanten der Untermatrizen zu berechen kannst du wieder den Laplace Entwicklungssatz anwenden oder du verwendest die Regel von Sarrus, deren Vorgehensweise du im Artikel zur 3×3 Determinante nachlesen kannst. Damit bekommst du




Zum Schluss kannst du nun die Determinante der Matrix A berechnen



Weitere Themen zur Determinante
Neben dem Thema „Laplacescher Entwicklungssatz“ haben wir noch weitere Themen für dich vorbereitet, die sich mit der Determinante beschäftigen. Schau dir unbedingt auch unsere Videos zu den folgenden Themen an:


