Spur einer Matrix
In diesem Beitrag beschäftigen wir uns mit der Spur einer Matrix. Wir zeigen dir wie du sie berechnen kannst und welche Eigenschaften sie besitzt. Schau dir unser Video dazu an!
Inhaltsübersicht
Spur einer Matrix einfach erklärt
In Worten gefasst entspricht die Spur einer Matrix  der Summe der Elemente entlang der Hauptdiagonale dieser Matrix
der Summe der Elemente entlang der Hauptdiagonale dieser Matrix  .
.
Die Elemente entlang der Hauptdiagonale sind dadurch charakterisiert, dass beide Indizes, die den Standort des Elements innerhalb der Matrix festlegen, denselben Wert annehmen.
Wenn wir die Elemente von  entlang der Hauptdiagonale mit
entlang der Hauptdiagonale mit  bezeichnen, dann kannst du die Spur folgendermaßen berechnen.
bezeichnen, dann kannst du die Spur folgendermaßen berechnen.

Beispielsweise ergibt sich für die Matrix

die Spur aus der Summe der Diagonalelemente
 .
.
Weitere Notationen für die Spur sind spur, spr, Sp, sp oder auch Trace, trace, Tr oder tr für die englische Bezeichnung trace.
Beispiel 1: Spur einer 3×3-Matrix
Wir haben folgende Matrix gegeben
 .
.
Die Elemente entlang der Hauptdiagonale lauten
 und
und  .
.
Damit ergibt sich die Spur von  zu
zu
 .
.
Beispiel 2: Spur einer 4×4-Matrix
Wir haben folgende Matrix gegeben.

Die Elemente entlang der Hauptdiagonale lauten
 und
und  .
.
Damit ergibt sich die Spur von  zu
zu
 .
.
Spur Matrix Eigenschaften
In diesem Abschnitt geben wir dir eine Auflistung verschiedener Eigenschaften, die die Spur besitzt.
- Eigenwerte und Spur Matrix: Die Spur einer Matrix entspricht der Summe ihrer Eigenwerte .
- Charakteristisches Polynom und Spur Matrix: Wenn du das charakteristische Polynom einer quadratischen Matrix berechnest, wirst du feststellen, dass der zweithöchste Koeffizient dieses Polynoms gerade das Negative der Spur der dazugehörigen Matrix ist.
-
Transponieren und Spur Matrix: Die Spur einer Matrix
 und die Spur der transponierten Matrix
und die Spur der transponierten Matrix  sind gleich, das heißt, es gilt:
sind gleich, das heißt, es gilt:
 .
. -
Lineare Abbildungen und Spur Matrix: Die Spur einer Matrix ist eine lineare Abbildung, das heißt es gilt:
 .
. -
Kommutativität und Spur Matrix: Die Multiplikation zweier Matrizen muss nicht unbedingt kommutativ sein. Unter der Wirkung der Spur, kannst du aber die Matrizen vertauschen und das Ergebnis bleibt dasselbe, auch wenn die Größe der resultierenden Matrix unterschiedlich sein kann. Konkret gilt:
 ,
,
wobei und
und  Matrizen mit der „richtigen Größe“ sind, sodass die beiden Produkte
Matrizen mit der „richtigen Größe“ sind, sodass die beiden Produkte  und
und  definiert sind und quadratische Matrizen ergeben.
definiert sind und quadratische Matrizen ergeben. -
Definitheit und Spur Matrix: Sind
 und
und 
 -Matrizen und ist
-Matrizen und ist  positiv definit
und
positiv definit
und  nicht negativ, dann gilt:
nicht negativ, dann gilt:
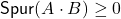 .
. -
Ähnliche Matrizen: Die Spur zweier zueinander ähnlichen Matrizen ist gleich, das heißt, es gilt:
 ,
,
wobei eine
eine  -Matrix und
-Matrix und  eine invertierbare
eine invertierbare  -Matrix ist.
-Matrix ist.
 ,
,